
книги из ГПНТБ / Мания, Г. М. Статистическое оценивание распределения вероятностей
.pdf
|
Т е о р е м а |
5.1. |
Если |
|
||
1. |
Е ? = 0 ; |
|
|
|
|
|
|
___ |
О / 1 |
\ |
3— |
||
2. |
Е (0f — ©,)•= |
|||||
|
|
|
Ы |
’ |
‘ |
'm; |
3. |
ailpq(x; t), i, |
/, |
p, |
q = |
1 ,m, |
непрерывны no t |
4. |
[ j 2(x)dP = 0\ |
:E ) • |
|
|
||
|
1 |
I |
|
|
|
|
|
•j |
|
|
|
|
|
Ac
где Ап—цилиндр в (/?'1)со, основание которого находится в (Rk)n и состоит из тех точек, для которых
0' n 6 V e i e o = { < : I f - e I < e 0} , s 0< e ,
то
т
Е T (x)4(x) + Y |
^ a j7(% ;0) |
Е ( 0 , - 0 , ) ( 0 , - 0 ; ) + |
|||
|
|
|
i j = l |
|
|
т |
|
|
- |
|
|
+ Т w |
a i } p ( x ; |
e ) E |
( 0 / - 0/)< ® p - 0 p )’ + . 0 Ы ) |
(5 -2 -2 > |
|
i,j,P= 1 |
|
|
|
|
|
U |
|
m |
|
|
|
|
|
|
|
|
|
|
D 'fix) = |
a, (x; 0) a.j(x; 0) E |
(0,—0г) (fy—07) |
4- |
|
t,/=l
m
+2 at(x; Q)a}p(x-, 0> E fa -W B j-Q ,){% -&,) +
*,/.P=l
|
+ 0 ( i , j . |
^ |
<5.2.3, |
|
З а м е ч а н и е . |
Из условия |
3 вытекает существование ко |
||
нечной функции G(x; 0), которая |
при t^V e^o и |
всех х огра |
||
ничивает сверху |
абсолютные |
значения |
f(x; t) |
и ее частных |
производных по t до четвертого порядка включительно. |
||||
Д о к а з а т е л ь с т в о . Так как, согласно неравенству Гель- |
||||
дера, из условия 2 |
следует, что |
|
|
|
1Е0 |
|
|
|
|
Е П (0'г - |
% ) < Е П | 0 , - % |
г= 1 |
г= 1 |
г Р |
1/6 = 0 ^ 1 |
|
|
Lr = l |
( tlpk |
|
то по неравенству Чебышева
Р {Ас„ } = Р {10 - |
0| > г0} < |
г0~6 Е |0-0|« = |
|
|
ш, |
|
|
= £Г6 Е |
2 |
( в / - 0/)2 |
= О ( — }. |
|
73 |
||
i = 1
Из (5.2.5) и условия 4 вытекает
(5.2.4)
(5.2.5)
f(x )d P ^ ( Р(х) dP |
dP |
= |
|||
Лс |
|
А*' |
|
Ас |
|
sin |
|
sin |
|
s*n |
|
— О ( — ) |
|
[Р (А'п)]Ч, = |
0 |
( - } - |
(5.2.6) |
п / |
|
|
|
\ п°12 |
|
■откуда |
|
|
|
|
|
•Е f(x) = |
j |
? (* ) |
j* ? (* ) dP -f J /(X) dP: |
||
■ ( « * ) * |
An |
Acn |
|
||
= j |
? ( * ) dP + 0 ( ^ - |
|
(5.2.7) |
||
Постараемся получить |
аналогичное представление |
и для D fix). |
|||
Считая (5.2.2) доказанным, из (5.2.4) |
имеем |
|
|||
Е /(* ) = /(* ) + |
0 ' |
1 |
|
||
Следовательно, |
|
|
|
|
|
D /W = Е [Т (х )-Е ?(х )Р = Е / ( x ) - / ( x ) + О
= ,Е [/( х ) - Д х )]2+ 0
151
Поскольку, согласно (5.2.5), (5.2.6) и условию 4,
\ f(x)-f{x)fd P = |
[j> {x )d P - 2 f{x ) |
я-п |
fin |
А с |
А с |
1 '
- / 2W J dP = О w
Асп
ТО
D / (*) = \ [f{x )-n x )fd P + 0
An
В силу (5.2.5) и условия 2,
| Т(х) dP+
finA c
(5.2.8)
f |
П № v - % ) |
^J |
.t* |
|
II |
|
О |
dP |
П ( 0 ц - 9 ц rdP |
|
V/ |
|
r = 1 |
р /«
о Ш Г р/, - о ( Л ) ,
dP i-р/.
fiА Пс
/?=0’ з>
откуда следует, что
f П^ - %)dP=ЕП |
- ь )+ |
|
V =1 |
' =1 |
|
4 o ( L y |
р= ОТз. |
(5.2.9) |
Для подсчета j / (х) dP подынтегральную функцию пред
ал ставим по формуле Тейлора е остаточным членом в форме Лаг
ранжа с четвертыми производными
|
|
m |
|
|
^J(x)dP = f(x) j1 dP+ |
at(x\ 0) |
j*(0 ,--0f) dP + |
||
An |
An |
i==1 |
|
An |
m |
|
|
|
|
- f y 2 |
Щ,(х\ |
ft) j f o |
- 0/) (0y |
0j) dP + |
«• /=1 |
|
Лл |
|
|
152
+ ~ |
|
aliP(x;Q) |
j, (0/- 0 /)(0/- 0 /)(0„-0p)rfP + |
i, /, |
р=1 |
|
An |
+ Y 4 |
У ] |
J W |
* ’ 0 * W ) ( 0 t - 0 i)(0 / - 0 / )'(0p |
«. /. |
p. |
|
|
—0p)(0q —0q)
где 0*(x) лежит на отрезке, соединяющем 0 и 0. Из (5,2.4) и-
условия 3 следует, что последняя сумма является О 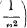 . Сог
. Сог
ласно (5.2.9), интегралы во всех предыдущих суммах равны математическим ожиданиям от подынтегральных выражений с
точностью до О . Теперь для получения (5.2.1) остается
применить (5.2.7).
Перейдем к доказательству (5.2.3). На множестве Ап, 0(ху представим по формуле Тейлора с остаточным членом в форме Лагранжа с третьими производными в точке 00* (х) (0* (х) находит
ся на отрезке, соединяющем 0 и 0). Согласно замечанию к. теореме и соотношению (5.2.4),
-(—— aijp(x’ 0о(л'))(0г 0()(6/ 0/)(0р 0>) dP—
т
153,
т
~v
откуда., применяя (5.2.8) и (5.2.9), получаем (5.2.3). Теорема доказана.
Теорема 5.1 не претендует на большую общность, но она полезна хотя бы потому, что в ее схему хорошо вписывается обычная параметрическая оценка многомерного нормального рас пределения (глава VI) и с помощью этой теоремы существенно упрощается подсчет ее моментов.
§3. РАСПРЕДЕЛЕНИЕ НЕКОТОРЫХ ФУНКЦИИ ОТ НОРМАЛЬНЫХ
ИАСИМПТОТИЧЕСКИХ НОРМАЛЬНЫХ СЛУЧАЙНЫХ ВЕКТОРОВ
Впоследствии мы часто будем сталкиваться с квадратич
ными формами от нормальных случайных векторов, которым посвящено несколько теорем, приводимых ниже.
Пусть случайный |
вектор |
У £ Rm имеет |
многомерное нор |
||||
мальное распределение |
N (О, |
С) |
с нулевым |
вектором |
средних |
||
значений и невырожденной матрицей ковариаций |
С. Заметив, что |
||||||
все рассматриваемые векторы—столбцы, обозначим S |
симмет |
||||||
ричную матрицу myi.ni с действительными элементами. |
|
||||||
Т е о р е м а 5.2. Если |
Y имеет распределение N(О, |
С), то |
|||||
|
|
|
т |
|
|
|
|
Y’SY= ^ |
\Z\, |
|
|
(5.3.1) |
|||
■где Zly..., Z m -независимые случайные величины, |
распределенные |
||||||
N(0, 1), а Я.1,...,Х т суть корни уравнения |
|
|
|
||||
|
I 5 - Х С - 1! = 0 . |
|
|
(5.3.2) |
|||
Д о к а з а т е л ь с т в о . |
Как |
известно |
из |
теории |
матриц, |
||
существует невырожденная |
матрица А такая, |
что |
|
||||
154
11
A'C-1A = I,
где / —единичная матрица, а Хх.,..., \т—корни уравнения (5.3.2) [2]. Все эти корни вещественны, и очевидно, что количество нерав
ных нулю среди них равно рангу матрицы |
5 . Когда S неотрица |
|||||||||||
тельно определена, все неравные нулю X,- положительны. |
||||||||||||
|
Обозначим Z=A~l Y. Z имеет распределение Л/(0, Л-1С(Л"1)/, |
|||||||||||
т. е. N(О, I) |
[1]. |
|
Так |
как |
Y'SY^Z'A'SAZ, |
то |
(5.3.1) оче |
|||||
видно. |
|
|
Если |
т-мерный |
вектор |
Y |
распределен |
|||||
|
С л е д с т в и е . |
|||||||||||
N (О, С), то |
Y' С"1 |
Y |
имеет у2 распределение с |
т степенями |
||||||||
свободы. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Согласно теореме 5.2, для того, чтобы найти |
распределе |
||||||||||
ние |
квадратичной |
формы Y'SY от компонент случайного векто |
||||||||||
ра, |
распределенного |
N(О, С), |
нужно уметь находить |
распреде |
||||||||
ление линейной комбинации |
квадратов |
независимых |
случайных |
|||||||||
величин, распределенных N (О, 1). Общие |
формулы |
для функ |
||||||||||
ции |
распределения |
таких |
|
комбинаций |
даются |
в работе [83] |
||||||
для случая положительных |
X,. |
|
|
|
|
|
||||||
|
Т е о р е м а |
5.3. |
Функция распределения |
случайной вели- |
||||||||
личины |
|
|
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
\ z i
i= l
где Хг> 0 , i=\,m, a Zx,..„ Zm—независимые случайные величины* распределенные N (0, 1), равна
UV |
|
I |
|
|
F(x)-- |
|
|
i Ус* <?Л +1/( - i . |
(5.3.3) |
1=0 |
/= 0 |
|
|
|
где Gf (x)—функция распределения |
у 2 с / степенями свободы, |
|||
X—произвольное число такое, что |
|
|
||
|
|
1 |
|
|
|
|
щах Х(-, |
|
|
|
|
2 |
i |
|
at~ коэффициент г* в разложении |
|
|
||
|
Ш |
|
Рр гр\ |
|
|
u |
2 * |
|
|
|
i— 1 |
р = о |
|
|
155
здесь
а / = Л/- |
Рр ( — |
Ср |
Для вычисления F(х) важно, что погрешность приближе ния ряда (5.3.3) его частной суммой равномерно по х стремит ся к нулю при дополнительном ограничении на А
— |
max А, < А < |
min А,. |
(5.3.4). |
|
3 |
i |
1 |
i |
|
При условии (5.3.4) для остатка Rp(x) ряда (5.3.3) имеем |
||||
sup RJx) |
< А Р = - |
|
X |
|
0<х<( |
|
~ ъ т г / п + 3 |
||
|
|
у |
к 0” /3 Г “ |
4 |
|
|
|
|
|
|
|
|
я + |
2 |
X |
р+1 |
1 |
- + |
(5.3.5): |
|
Н И - Т ) |
Г ( А |
||
|
|
|
||
где о = max — . i а
Следует отметить, что в работе Гурланда [83] допущена ошибка: в правой части формулы (10) на стр. 39, выра жающей F (х), слагаемое 1/2 излишне.
Рассмотрим теперь последовательность случайных векторов
У „ € Я га, « = 1 ,о о , |
и постоянный вектор |
a £R m. Нас интересует, |
||
предельное |
распределение функции от |
Yn при условии слабой |
||
сходимости |
распределения |
вектора ] / |
п (У „—а) к N(О, С). |
|
Т е о р е м а |
5.4. Пусть |
распределение случайного вектора |
||
У п (Yn—a) слабо сходится к N (О, С) uw(u) есть функция от и= (и1,..., ит), которая в окрестности точки а имеет непре рывные частные производные.
/ |
dw \ |
/ dw |
ненуле— |
а) Если вектор grada w= |
/а |
— |
|
\ |
\ |
|
вой, то распределение случайной величины
V П(ву(Уп) —ш.(а))
слабо сходится к N (0, (g ra d ^ )' Cgrada w).
156
б) Если же gradany = 0, и в окрестности точки а сущесгтвуют непрерывные частные производные w{u) второго порядка, причем значения последних в а не все равны нулю, то распре деление случайной величины
n{w (Yn)-w (a ))
слабо сходится к распределению квадратичной формы
т |
|
JL V ( ^ ) |
Y.Y. |
2 jmJ \дщди, |
а 7 |
г, /= 1 1 1 |
“ |
от компонент случайного вектора Y с распределением N (О, С).
При доказательстве этой теоремы используются формула Тейлора с дополнительным членом в форме Лагранжа и свойст ва эквивалентных по вероятности последовательностей случай
ных величин. Нужно учесть, что из наличия у вектора Уп(Уп—а) предельного распределения следует сходимость по вероятности
случайного вектора Yn к вектору а при |
и |
со. |
|
|
Теоремы, аналогичные теореме 5.4, |
а |
также |
некоторые |
|
ее обобщения с |
использованием высших |
производных |
читатель |
|
может найти в |
[1, 14, 63, 68]. |
|
|
|
§ 4 . ПРЕДЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ СРЕДНЕЙ КВАДРАТИЧЕСКОЙ ПОГРЕШНОСТИ ПАРАМЕТРИЧЕСКОЙ ОЦЕНКИ ПЛОТНОСТИ РАСПРЕДЕЛЕНИЯ
Т е о р е м а 5.5. Если |
|
|
|
|
|
1° |
почти всюду по х, |
| ас(x; |
t) |^ G (х; |
0) £ L3 |
при t 6 f/e,8 |
и а{(х; |
t) непрерывна по t |
в i / 0/e, £ =l,m; |
|
|
|
2° распределение случайного вектора У |
п (0 — |
0) = Vn = |
|||
= (V ln,..., Vmn) слабо сходится к N (О, С) при п-*-со, |
|||||
то |
lim Р {<J>(0)<w} = .F(u), |
|
(5.4.1) |
||
|
|
||||
|
П — 00 |
|
|
|
|
где F(а)—функция распределения |
неотрицательно определенной |
||||
квадратичной формы |
т |
|
|
|
|
|
|
|
|
|
|
|
A(V; 0 ) = 2 ] |
л о ( 0) Vtv i |
|
||
£J=1
от компонент вектора V=(Vv ..., VУ) с распределением АГ(0, С),
157
где
Atj (0) = |
\щ(х\ 0) £*/(*; Q)dx. |
|
(5.4.2) |
||||||
Д о к а з а т е л ь с т в о . |
По |
формуле |
Лагранжа |
почти для |
|||||
всех х |
|
|
|
т |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
f(x; t ) - f ( x ; |
0 )= ^ £ J |
«Д *; 6(*> |
0 )(^ -9 г ). |
|
(5.4.3) |
||||
|
|
|
i= l |
|
|
|
|
|
|
где точка 0(х, |
лежит внутри отрезка прямой, соединяющей 0 |
||||||||
и t. Отсюда и из |
условия |
2° |
получается, |
кстати, |
что |
f(x;t)~ |
|||
—f(x\ 0 ) £ L 2 при |
t£Ue,е- |
|
|
|
|
|
|
||
С вероятостью |
Р(0£^й,еК |
стремящейся, по |
условию 2°, |
||||||
к 1 при п—>~со, верно |
соотношение |
|
|
|
|||||
ф ( 9 ) = ^ |
^ |
|
/n j |
йДх ; 0 (jc, 0)) aj{x; Q(x,Q))dx. |
|||||
i,i= 1 |
|
|
|
|
|
|
|
|
|
Отсюда, применяя теорему о мажорированной сходимости интег ралов Лебега, получим, что предельнее распределение Ф(0) сов падает с распределением Л(П; 0). Теорема доказана.
Заметим, что при любом V
0 < Л ( П ; 0) = J [V'grade f(x; t)\2 dx.
В |
теореме |
5.5 |
мы |
не располагали |
явной |
зависимостью |
Ф (0) от |
0 и нашли |
его предельное распределение, минуя ре |
||||
шение интеграла. |
Если же |
вычислить Ф(0), |
то |
очевидно, что |
||
поиск его предельного распределения вписывается в рамки тео
ремы 5.4 с функцией |
|
® (0 = J [/(х ; 0 —/(*; 0)? dx. |
(5.4.4) |
При этом оДв) = 0 и, поскольку при ^=0 налицо минимум, то, если первые производные по параметру существуют, они равны нулю в точке 0.
Продифференцируем теперь w(t) формально два раза:
~ = 2 j [/(*; 0)]аД х; t) dx,
158
<j2tl> (О |
2 |
{[/(*; |
0)] aif(x; |
t)+ai(x; |
£)} dx. |
|
|||
dt{dtj |
|
||||||||
|
|
|
|
|
|
|
|
||
Следовательно, |
если |
вдобавок |
к условию 1° |
теоремы 5.5 |
пот |
||||
ребовать |
выполнение |
условия |
|
|
|
|
|
||
3° |
почти |
всюду по х, |
| аг ■(х, t) |
| ^ |
6\ (х; |
8) £ L2 |
при |
||
^6 Я е.Е, С / = Г т ,
то grade да = 0 и частные производные непрерывны в U0>е, причем
1 dw
2 |
= A /(9\ |
dtjJ e |
второго порядка w(t)
(5.4.5)
Итак, верно следующее |
|
|
|
З а м е ч а н и е к |
т е о р е м е |
5.5. Если выполнены |
условия |
1° и 2° (теорема 5.5) |
и условие |
3°, то коэффициенты |
предель |
ной квадратичной формы для случайной величины пш(0) = Ф(9), подсчитанные при помощи теоремы 5.4, совпадают с коэффици
ентами, установленными в теореме 5.5, т. |
е. верно соотноше |
||||
ние (5.4.5). |
Н (х, 0)—некоторая |
|
|
|
|
Пусть |
неотрицательная |
функция от |
|||
x-£Rh, зависящая от параметра 0. Обозначим |
|
||||
Ф(0; Н) = п y f(x ) - f(x )}2 Н(х; |
0) dx. |
(5.4.9) |
|||
Последняя |
статистика |
является |
взвешенной с функцией Я (х ; 0) |
||
с. к. п. оценки 0(х). |
Очевидно, |
что |
|
|
|
Т ( 0 ) “ Ф ('е ; ДДе>
Пусть g (х) £ Е2(Н) для функции g (х) означает, что
g2(х) Я (х; 0) Ф х<со.
Ясно, что с очевидными изменениями в формулировке тео
рема 5.5 верна |
и для |
Ф(0; |
Я). |
|
|
|
||
Т е о р е м а |
5.9. |
Если |
выполнены |
условия |
2° и |
|||
4° |
почти |
всюду |
по |
х, |
| щ(х; /) |
| ^ |
G(х; |
0) 6 L2 (Я) при |
и аг(х; |
t) H V B,e непрерывна |
по t в UBri, |
t= l,m , |
|||||
то |
|
lim Р (Ф(0; |
Н)<Си} = Ен (и), |
|
(5.4.7) |
|||
|
|
|
||||||
|
|
Я — со |
|
|
|
|
|
|
159
