
книги из ГПНТБ / Реология в процессах и аппаратах химической технологии [сборник статей]
..pdfЗдесь: а — тензор напряжений;
Р— гидростатическое давление;
б— единичный тензор;
|
F — симметричный, |
матричный, полиномиальный |
В! |
функционал; |
тензоры. |
Вп — кинематические |
Из работы [2] для данной кинематики течения получим реологическое уравнение состояния, связывающее динамиче ские и кинематические характеристики движения среды по поверхности вращающегося диска в виде:
РО 0 |
|
г * , # |
(Эфг&уф(5уг *- 0 Р 0 |
+ 0 0 |
0 |
б г г б г у б гг 0 0 р |
|
« |
р — коэффициент, определяющий величину нормаль ных напряжений на площадках, перпендикуляр ных к главным линиям тока.
р ф ; |
«) |
(г |
|
где цЭф — эффективная вязкость, |
модулю |
G — константа материала, пропорциональная |
|
сдвига. |
|
Известно, что наиболее простой и хорошо коррелирующей с экспериментальными данными формой описания нелинейно вязких свойств материалов в широком диапазоне скоростей сдвига является степенной закон Оствальда де Виля. Для на шего случая получим:
60
(5)
С учетом 'принятых допущений уравнения движения в напря жениях запишутся в виде:
ЭРдЭГгг , Ьг |
♦ |
d t z t |
; |
|
дг дг |
е |
д2 |
||
(ч )
Подставляя (1), (2), (3) в уравнение (4), получим:
Эр К1 Ъ
э г “ <> зг'Эг
(О
Уравнение неразрывности запишем о интегральной форме
к |
|
Q* i £ z f e d l t |
|
о |
|
где Q — радиальный расход среды. |
ищем в виде: |
Решение системы уравнений (5) — (6) |
|
1 |
(7; |
f—n r — |
zSe
Здесь: p — плотность среды, n — индекс течения, к — характе ристика консистентности.
Избавляясь от давления перекрестным дифференцировани ем уравнений (5), (6) с учетом (7), получим:
2л 2/t-М а /а<в.2+
2а W M >
+каa+zоу(Iгъ 31
здесь |
(8) |
61
Полагаем
Тогда из уравнения (8) получим:
и " + А и и ' - а и = о . |
в ) |
Штрих в уравнении (9) означает дифференцирование по Z0.
/ b - g a j W '* , |
ОО) |
Уравнение (9) не интегрируется в квадратах. Применим приближенный метод решения. Введем подстановку: и*=У. В этом случае из уравнения (9) найдем:
V M + A l U f - b l L = 0. |
СЮ |
аа
Вуравнении (11) переменные разделяются. Проведенный анализ показывает, что для реальных процессов течения вели чина В (10) исчезающе мала. Полагая В равным нулю, из
уравнения (11) получим:
f c - j r A U 1* С, |
СЩ |
где с — константа интегрирования. Из уравнения (12) найдем:
IL'+fAU^C. (15)
Уравнение (13) является частным случаем специального уравнения Риккати. Интегрируя уравнение (13) с учетом гра ничного условия: при z0 = h-a, U = 0, получим:
U= |
C ,th.|/pC ^ |
и |
(i0-ha)- |
Из уравнения (14) с учетом зависимости (7) и (8а) и гра ничного условия при zo = 0, Vr = 0, найдем:
62
Подставляя значение Vr из (15) |
в уравнение (5) и учиты- |
||
, |
dP |
„ |
|
вая, что при z = h, |
|
=0, с достаточной степенью точности |
|
найдем константу |
интегрирования |
в виде: |
|
|
|
i-a. |
|
|
|
С г - Ъ г , |
|
tde
В этом случае для радиальной скорости получим зависи мость:
где у ,_А£(Ь0)г |
(16) |
||
2 & {a J |
|
||
Из уравнения (16) видно, |
что чем ярче выражены упругие |
||
свойства среды, тем меньше радиальная |
скорость, т. к. Угр |
||
растет гораздо быстрее, |
чем th у-ф. Расход среды найдется в |
||
виде: |
|
|
|
о |
|
> |
(17) |
|
|
|
|
Подставляя в это выражение значение |
Vr из уравнения |
||
(16), получим: |
га*1 |
|
|
№ |
> |
(18) |
|
й = В г л к: п. |
|
||
где
Из уравнения (18) найдем зависимость для толщины пленки
(19)
к=[ 6 г^
/
ВЫВОДЫ1
1. Получено распределение радиальной скорости по тол щине пленки жидкости от основных интегральных параметров
63
центробежной -насадки. Чем ярче выражены упругие 'Свойства среды, растекающейся по вращающемуся диску, тем меньше радиальная скорость.
2. Получена зависимость толщины пленки вязкоупругой среды от основных интегральных параметров центробежной насадки.
ЛИТЕРАТУРА
1.White J. L. X, Appl. Polym. Sci. 8, 1129 (1964); 8, 2339 (1964).
2.Ремнев В. П., Тябин Н. В. Распределение скоростей и давления при течении вязкоупругой жидкости в зазоре дискового экструдера. Механика полимеров. 3, 515, 1971.
64
ОГАРЕВ Н. В., СУРГАНОВА Т. А.
МЕТОДИКА РАСЧЕТА ПОЛЯ СКОРОСТЕЙ ТЕЧЕНИЯ ЖИДКОСТИ
ЧЕРЕЗ ПОПЕРЕЧНОЕ СЕЧЕНИЕ ЦИЛИНДРА
Распределение скоростей несжимаемой маловязкой жид кости (типа воды) при диаметральном перетекании в цилинд ре представляет интерес при проектировании различных аппа ратов. Например, теплообменников, химических реакторов, колонных аппаратов и др. Принимая во внимание трудность аналитического решения задачи, предлагается ее решение произвести с использованием опытных данных.
Предполагается, что течение происходит по схеме, приве денной на рис. 1, то есть по существу сводится к циркуляции двух симметричных вихрей, питаемых энергией основного потока.
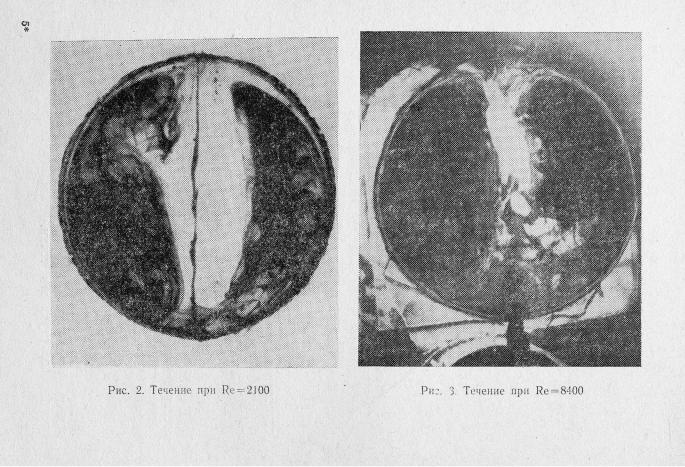
Такое представление подтверждается фотографиями пото ков трассирующей жидкости, полученных в прозрачных моде лях в момент ее ввода в основной поток, рис. 2, 3.
С целью упрощения можно допустить, что в вихрях про исходит незатухающее вращение идеальной жидкости.
Оба вихря по форме приближаются к эллипсу с размером малой оси 2d = R, т. е. радиусу цилиндра. Размер большой оси 2а может быть найден из уравнения для радиуса кривизны эллипса [1].
3
(1)
где Хс, Yc — координаты точки, в которой определяется радиус кривизны.
При
личина линейной скорости |
течения от периферии эллипса к |
его центру в силу сдвига |
между слоями убывает в степенной |
5 Заказ № 154 |
65 |
Рис. 1. Схема перетекания жидкости через поперечное сечение ци линдра.
зависимое™ отношения радиусов [2], то есть пропорциональ-
н 0 |
е" |
(Где е — расстояние от рассматриваемой точки Е |
|
------ |
|||
|
Р |
|
|
до центра эллипса, р — соответственный |
радиус вектор эллип |
||
са, |
рис. 4), |
то скорость в точке Е можно |
выразить в виде: |
Показатель степени «п» может быть найден из замеров ско рости в каких-либо характерных точках. Например, точках
66
А и В. Тогда
о т к у д а .
( J )
Исходя, из уравнения (2), после преобразований величина ско рости Ve определяется как:
W . „ ' i f / |
W « Л |
А
Рис. 4. Эпюра скоростей в вихре.
Направление вектора скорости определяется ,по углу ф, составляемому им с осью Х-ов, и находится из уравнения касательной к эллипсу в данной точке «С».
X X c . l ^ c e l . |
|
|
С5) |
|
~oF~ |
Ьг |
|
|
|
Для отыскания |
входящих |
в |
уравнение (5) |
координат |
точки «С» по координатам (х, |
у) |
точки «Е» применены кано |
||
ническое уравнение |
эллипса и уравнение радиуса |
вектора, |
||
проходящего через |
эти точки. |
|
|
|
68
Величина угла ср находится из зависимости:
Ч а г с * « & ( й Н ф * | - ®
Например, при R= 1; n= l,2; x = 0,4R; у — —0,3R:
Ve = 0,65 Va и <р = 31°.
ВЫВОДЫ
1.Предложена методика описания поля скоростей при диаметральном перетекании через цилиндр для переходного режима (Re = 2000—8000).
2.Исходя из замеров скорости в характерных точках по формулам (4) и (6), могут быть найдены численные значения
инаправление векторов скорости для других точек поля.
ЛИТЕРАТУРА
1.Справочник по математике для инженеров и студентов втузов. М., «Наука». 1967.
2.Шлихтинг Г. Теория пограничного слоя. М., «Наука». 1969.
69
