matan_belaev_1.2 / 2MA_Lekc_3
.docРАЗДЕЛ 6. Бесконечные произведения.
§. ОБЩИЕ СВЕДЕНИЯ
Def:
Конструкция
вида
,
где
(или
)
называется бесконечным произведением.
При этом,
– общий член произведения, а
– частичные
произведения.
Def:
Если
,
то бесконечное произведение называется
“нулевым бесконечным произведением”.
Def:
Если
и
и
,
то бесконечное произведение называется
сходящимся к P.
Def:
Если
и
то произведение называется расходящимся
к нулю.
Рассмотрим
и перейдём к пределу при
.
Если произведение сходится то:
.
Получили: необходимое условие сходимости бесконечного произведения:
*. Если бесконечное произведение сходится, то его общий член стремится к единице.
Примеры:
1.
.
Частичные произведения
,
однако при этом
не стремится к единице. Не выполнено
необходимое условие сходимости
бесконечного произведения, хотя
.
Этот пример поясняет термин: «произведение
расходится к нулю».
2.
.
Казалось бы:
,
но
.
Бесконечное
произведение расходится, хотя 
при
,
т.е. стремление к единице общего члена
произведения, есть только необходимое,
но не достаточное условие сходимости.
*.
Каждому бесконечному произведению
можно поставить в соответствие
последовательность его частичных
произведений
и, наоборот:
.
Причём последовательность и произведение сходятся или расходятся одновременно (по определению), за исключением произведений расходящихся к нулю.
§. Достаточное условие сходимости бесконечного произведения.
-
Если ряды
и
– сходятся, то сходится и бесконечное
произведение
.
∆ Т.к.
сходится
то
.
Тогда
и,
значит,
и
сходятся или расходятся одновременно
но
сходится
–
сходится.
Тогда
и
-
сходится. ▲
Замечание:
Существуют
бесконечные произведения, для которых
и
–
расходятся, но
– сходится, т.е. теорема представляет
собой только достаточное, но не необходимое
условие сходимости. Здесь
привести такой пример.
§. Связь между рядами и бесконечными произведениями.
Записывая очевидное
равенство:
,
приходим к выводу о том, что
и
сходятся и расходятся одновременно
.
Def:
Бесконечное произведение
называется сходящимся абсолютно или
условно, если абсолютно или условно,
соответственно, сходится ряд
.
Примеры:
1.
Рассмотрим
.
Для его частичных произведений, получим:
=
=
=
=
=
.
Бесконечное произведение сходится, по определению.
2.
Рассмотрим
.
Для его частичных произведений, получим:
=
=
.
Произведение
сходится, если
.
При этом
.
§. Разложение sin x и cos x в бесконечное произведение.
Запишем формулу
Муавра
и возьмём мнимую часть от правой и левой
части равенства:
=
= …
Отметим что при
четных
слагаемые в сумме вещественны и,
следовательно, нас не интересуют, а при
нечетных
слагаемые чисто мнимые и, поэтому,
положив
,
продолжим выкладку:
… =
=
=
=
.
т.е.
.
Разложив
,
где
–корни
полинома
,
и отметив что, если
,
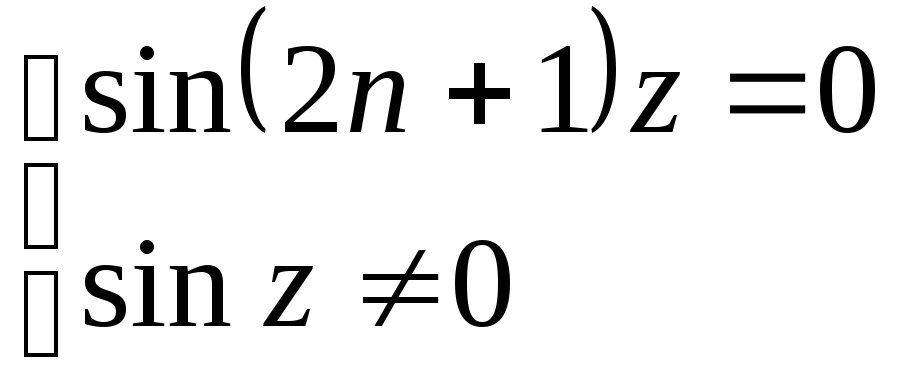то z
-корень
,
k
= 1,2,…,n.
Константа
.
Учитывая, что
делаем заключение:
.
Положим
и тогда, при фиксированном k
:
Тогда:
=
.
Чтобы рассмотреть
вспомним неравенство
.
Тогда:
и
.
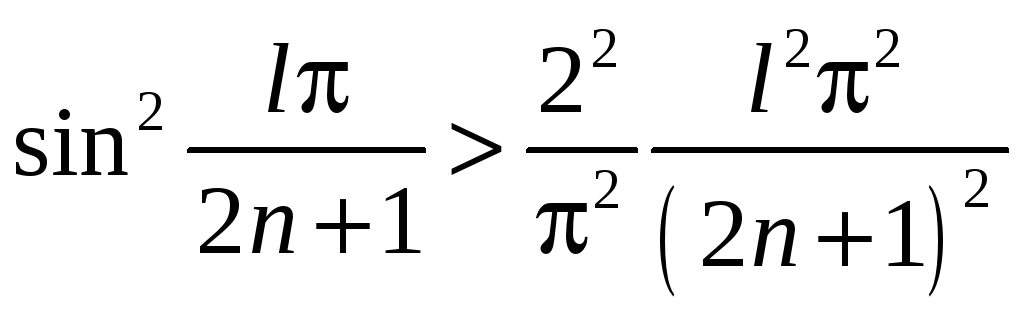Следовательно:
=
.
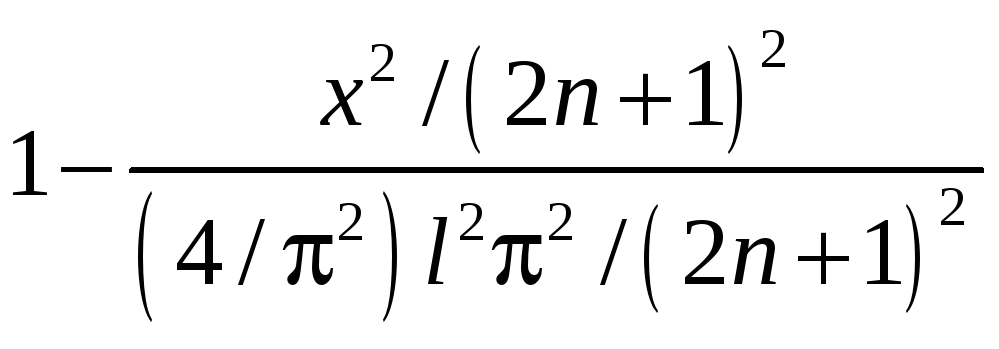Таким образом:
(*)
Бесконечное
произведение
сходится, ибо сходится ряд
.
(Здесь
выбрано так, чтобы
).
Поэтому остаточное произведение
должно стремиться к единице при
.
Очевидно, мы лишь усилим неравенство
(*), если напишем:
.
Переходя к пределу
при
и при фиксированном
,
получаем:
.
И, следовательно,
.
Мы приходим к разложению
в бесконечное произведение, впервые
полученное Эйлером:
.
Учитывая, что
и используя полученное разложение
в бесконечное произведение, можем
получить разложение
в бесконечное произведение.
В самом деле
.
Тоже самое
разложение можно получить и записав
,
а положив в разложении
,
получим формулу Валлиса:
=
.
§. Формула Стирлинга.
Запишем разложения
:
и
,
а после этого, вычтем из первого разложения
второго:
.
Положим в этой
формуле
.
Тогда:
и,
следовательно:
.
И, очевидно,
.
Оценка сверху для
дает следующее:
=
=
=
=
=
=
.
Из оценок для
,
получаем:
и, потенцируя:
.
(*)
Теперь рассмотрим
последовательность:
.
.
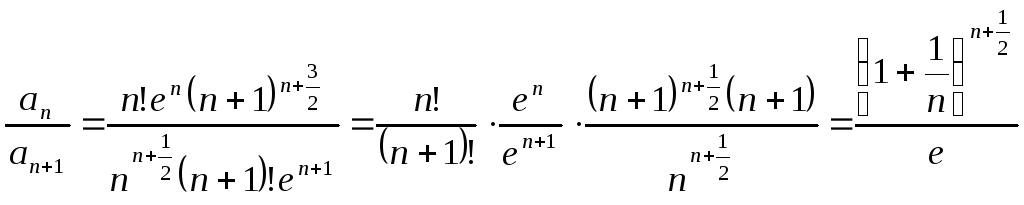учитывая (*),
получаем:
.
Таким образом:
и
.
Последовательность
возрастающая и ограничена сверху
.
Значит
и
,
т.е.
.
Для нахождения величины a воспользуемся формулой Валлиса:
.
=
=
=
= ….
Подставляя вместо
,
полученное для него выражение, получаем
.
Тогда:
.
Это и есть формула Стирлинга.
РАЗДЕЛ 7. ЭЙЛЕРОВЫ ИНТЕГРАЛЫ.
§. Гамма – функция Г(z).
Def:
.
1*. Прежде
всего отметим что функция не определена
при
.
Кроме того, если
то в бесконечном произведении найдется
член для которого
обращается в ноль и, следовательно,
бесконечное произведение не определено.
Для изучения
сходимости
рассмотрим сходимость ряда:
.
Для него
–
.
Из сказанного
ясно, что ряд, а вместе с ним и бесконечное
произведение, сходятся абсолютно, при
.
2*.
.
В самом деле:
=
=
.
3*. Формула
понижения:
.
=
=
.
Тогда:
.
Гамма-функция является, в некотором
смысле, расширением понятия факториала
на не целые значения аргумента.
4*. Формула
дополнения:
.
=
=
=
=
= ….
Полагая
,
получим и учитывая, что :
получим
….=
.
Из доказанной
формулы дополнения
:
• при
следует, что:
.
• при
получаем, что:
.
И, следовательно:
;
.
5*. Формула
удвоения:
.
6*. Формула
умножения:
.
7*.
Формула Лежандра (Эйлеров интеграл II
- рода):
.
8*. Бета-функция
(Эйлеров интеграл
I
– рода):
.
§. СВЯЗЬ МЕЖДУ ЭЙЛЕРОВЫМИ ИНТЕГРАЛАМИ I-го И II-го РОДА
=
=
=
=
.
Функция В(z,n) – называется Бетта-функцией.
§. БеТта
– функциЯ В(а,b)
.
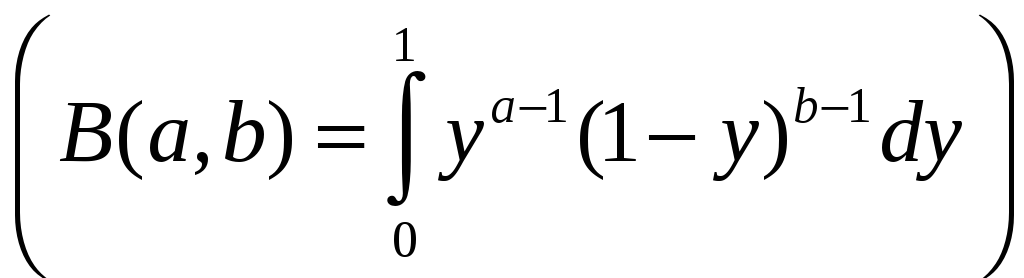Изучим свойства введенной функции:
а)
.
Δ
=
.
▲
б).
.
=
=
=
=
=
=
.
Отсюда
получается доказываемая формула.
Итак, имеем:
и
.
Если b
– целое число, то:
= … =
=
.
Если, при этом, а
– также
целое, то:
.
Эта формула
полученная для целочисленных значениях
аргументов справедлива и в общем случае:
.
в). Еще одно выражение для Бета-функции:
=
=
.
Т.е.
.
Кстати, при b
= 1 – a:
.
§. ЕЩЕ РАЗ Гамма – функция Г(z).
Возвращаемся к Гамма-функции. Нами установлено:
.
Последняя выкладка показывает, что функция, введенная в п.7, как эйлеровый интеграл 2-го рода, действительно совпадает с Гамма-функцией, определенной в начале раздела.