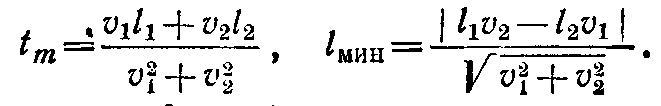workshops_2012-13(1) / 3_КинМатТ_ср,прямая и обр,extrem

4

Занятие 3. Кинематика материальной точки: среднее значение, прямая и обратная задача кинематики, задачи на extremum

Auditorium

1. Задача № 1.19 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.19.

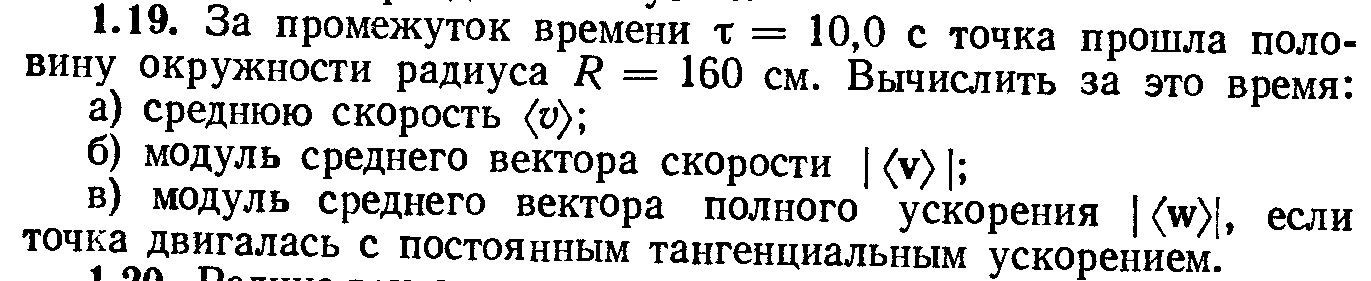
За час  = 10,0 с точка пройшла половину окружності радіуса R = 160 см. Знайти за цей час: а) середнє значення модуля швидкості; б) модуль середнього вектора швидкості; в) модуль середнього вектора повного прискорення, якщо тангенціальне прискорення було сталим.

2. Задача № 1.20 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.20.

Радіус-вектор частинки змінюється з часом за законом , де – сталий вектор,  – додатна стала величина. Визначити:

а) швидкість і прискорення частинки у залежності від часу ;

б) проміжок часу, по закінченні якого частинка повернеться у вихідну точку, а також пройдений при цьому шлях.

3. (При наличии времени)

Задача № 1.24 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Подобная задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.24.

Точка рухається у площині хy за законом , , де ,  – додатні сталі величини. Визначити:

а) рівняння траєкторії точки , зобразити її графік;

б) модулі швидкості і прискорення як функції часу ;

в) кут між векторами і як функцію часу .

4. Задача № 1.22 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.22.

Частинка рухається у додатному напрямку осі х, так що її швидкість змінюється за законом , де  – додатна стала величина. В момент частинка знаходилась у точці . Визначити:

а) її швидкість і прискорення як функції часу ;

б) середню швидкість за проміжок часу, протягом якого частинка здолає перші s метрів шляху.

5. Задача № 1.17 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.17.

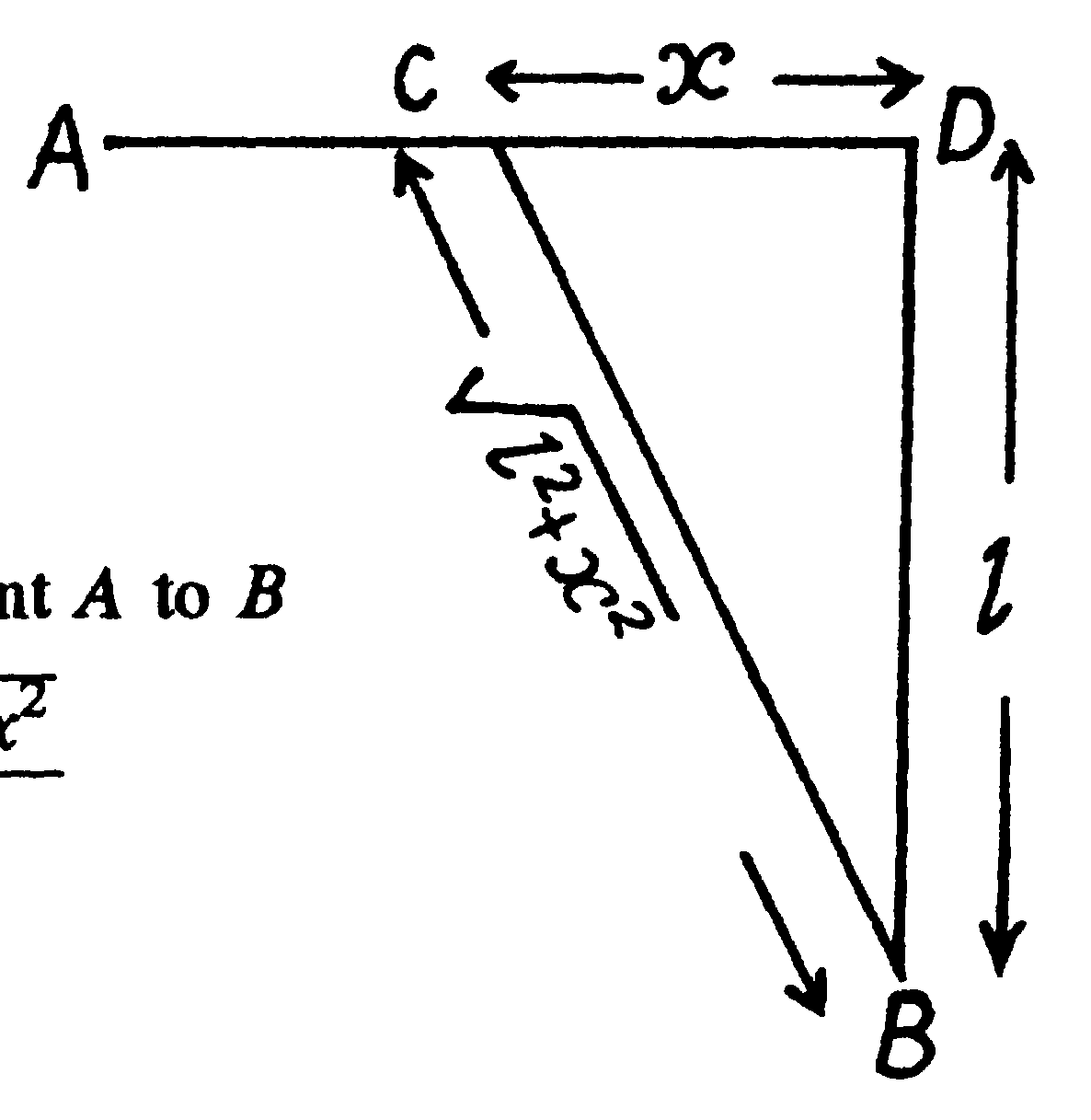
Із пункту А, який знаходиться на шосе (рис. 1.2), необхідно за найкоротший час дістатися на машині пункту В, що розташований у полі на відстані від шосе. На який відстані від точки D слід звернути з шосе, якщо швидкість машини по полю в разів менша за її швидкість по шосе?

Homework

1. Задача № 1.3 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.2.

Точка пройшла половину шляху зі швидкістю . На частині шляху, яка залишилась, вона половину часу рухалась зі швидкістю , а останню частину шляху пройшла зі швидкістю . Визначити середню за увесь час руху швидкість.

2. Задача № 1.21 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Подобная задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.21.

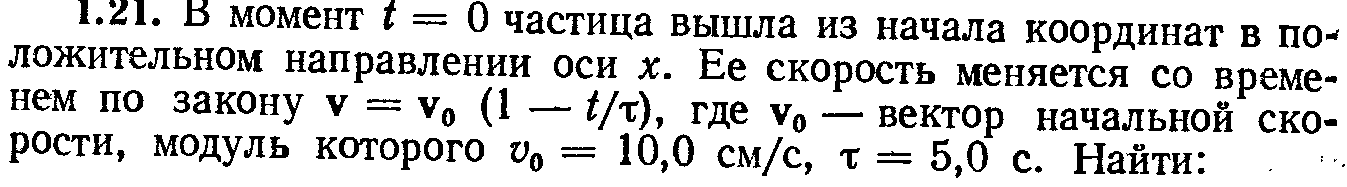
У момент часу частинка вийшла з початку координат у додатному напрямку вісі х. Її швидкість змінюється з часом як , де – початкова швидкість, її модуль , . Визначити:

а) координату х частинки, коли t = 6,0, 10 і 20 с;

б) моменти часу, коли частинка буде знаходитись на відстані 10,0 см від початку координат.

3. Задача № 1.23 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.23.

Точка рухається, сповільнюючись, по прямій з прискоренням, модуль якого залежіть від її швидкості як , де  –стала величина. У початковій момент швидкість точки дорівнює . Який шлях вона пройде до зупинки і за який час?

4. Задача № 1.25 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.26.

Точка рухається у площині хy за законом , , де А,  – додатні сталі величини. Визначити:

а) шлях , який точка проходить за час ;

б) кут між швидкістю і прискоренням точки.

5. Задача № 1.16 в кн. Иродов И.Е. Задачи по общей физике, 447 с. (Irodov_Zad.pdf)

Эта же задача в кн. Иродов И.Е. Задачи по общей физике, М., 1979, 369 с. – под номером 1.16.

Дві частинки рухаються зі сталими швидкостями і по двох взаємно перпендикулярних прямих до точки їхнього перетину О. У момент t=0 частинки знаходились на відстанях l₁ і l₂ від точки О. Через який час після цього відстань між частинками буде найменшою? Чому вона дорівнює?