
6 семестр (вечерка) / Теоретические основы электротехники / Курсовая работа / Курсовик Кондрашов
.docxМИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный
электротехнический университет
«ЛЭТИ» им. В.И. Ульянова (Ленина)
Кафедра теоретических основ электротехники
Курсовая РАБОТА
по дисциплине «Теоретические основы электротехники»
Тема: Анализ линейной цепи
Студент гр. 9802 |
|
Кондрашов Е. С. |
Преподаватель |
|
Яшкардин Р. В. |
АНАЛИЗ ЛИНЕЙЕНОЙ ЦЕПИ
Цель работы: усвоение различных методов качественного и количественного анализа линейной цепи.
ВАРИАНТ 4
Цепь задана тройкой чисел:
114 – ИН ;
224
–
;
224
–
 ;
313
–
;
313
–
 ;
432
–
;
432
–
 ;
534
–
;
534
–
 ;
624
–
;
624
–
 .
.
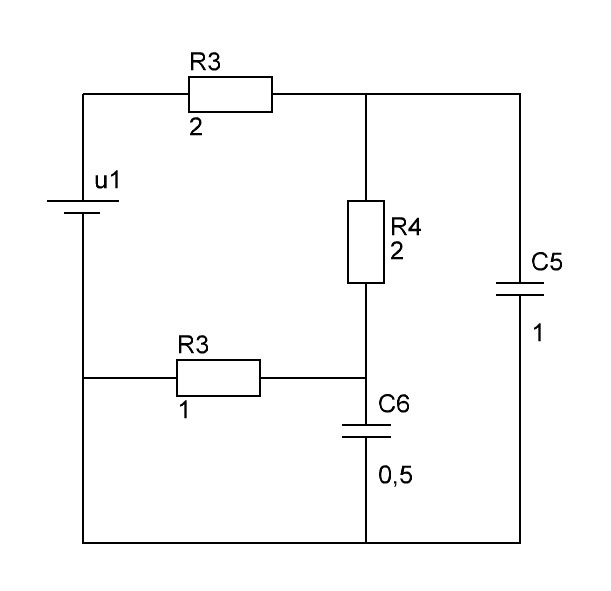


Рис. 1. Исследуемая цепь.
АНАЛИЗ ЦЕПИ ВО ВРЕМЕННОЙ ОБЛАСТИ
Исходные данные:
 в вольтах.
в вольтах.
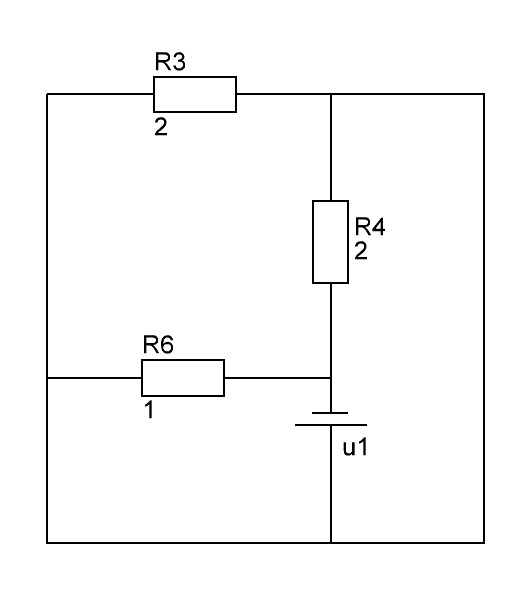
Составление уравнения состояния цепи для t ≥ 0.
Для составления
уравнения состояния заменим в исходной
цепи (Рис. 1) С – элементы источниками
напряжения
 Тогда цепь будет иметь вид (рис. 2):
Тогда цепь будет иметь вид (рис. 2):
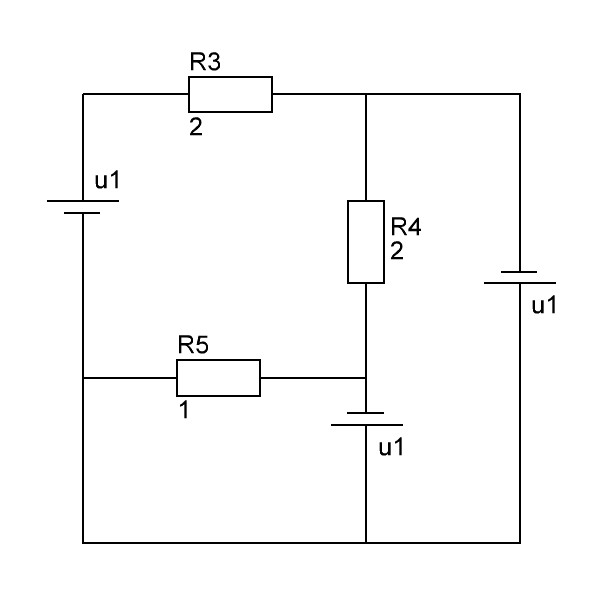
Рис. 2. Цепь с заменой С – элементов источниками напряжения.
Д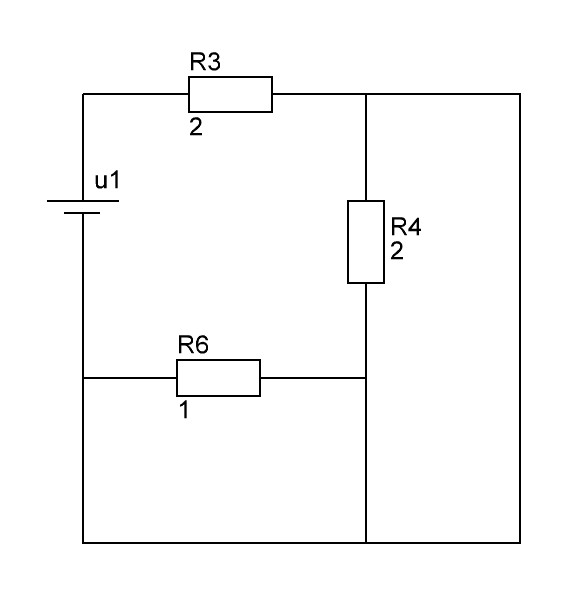 алее
применим метод наложения (поочередно
заменяем все источники кроме одного на
ИН – КЗ, ИТ – ХХ):
алее
применим метод наложения (поочередно
заменяем все источники кроме одного на
ИН – КЗ, ИТ – ХХ):


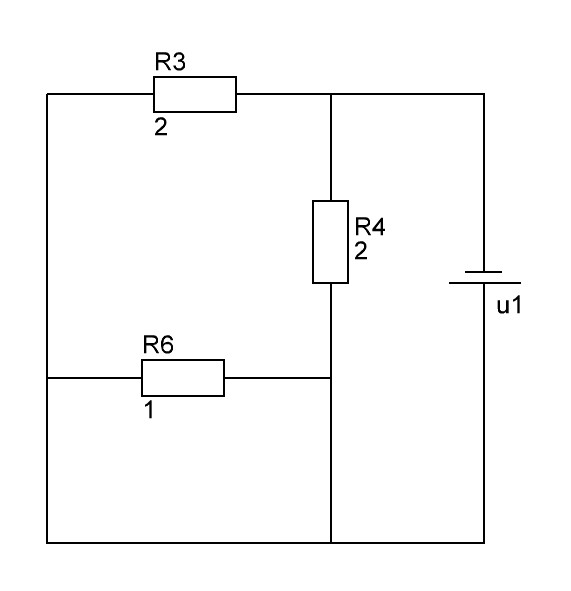







Р еакция
от действий нескольких источников равна
алгебраической сумме реакция от действия
отдельно взятых источников, тогда:
еакция
от действий нескольких источников равна
алгебраической сумме реакция от действия
отдельно взятых источников, тогда:




Далее составляем уравнения состояния:

Определение переходной характеристики
 и построение её графика.
и построение её графика.
Переходная
характеристика цепи
– это реакция цепи на воздействие
сигнала в виде единичной ступенчатой
функции
 .
В исследуемой цепи выходным сигналом
является напряжение нагрузки
.
В исследуемой цепи выходным сигналом
является напряжение нагрузки
 .
Так как
.
Так как
 решим уравнения
состояния относительно
решим уравнения
состояния относительно
 ,
приняв воздействие
равным 1 при
,
приняв воздействие
равным 1 при
 .
.
Для нахождения составим и решим характеристическое уравнение


Характеристическое уравнение:





Корни характеристического уравнения:


Общий вид решений уравнений состояния:

Находим вынужденные
составляющие при

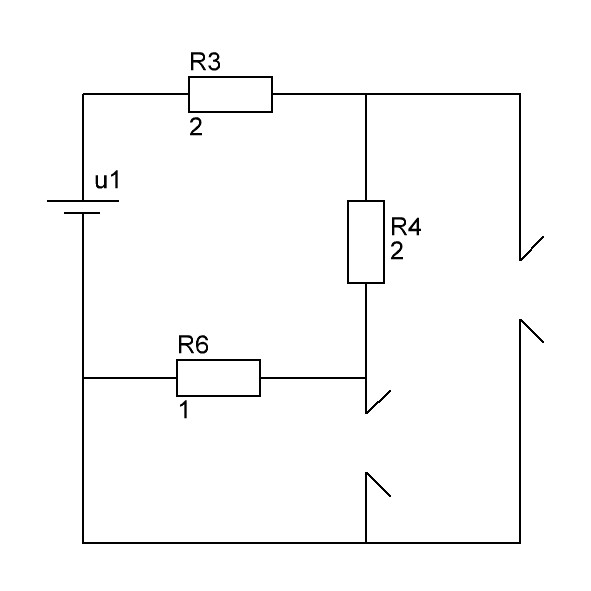
Рис. 6. Цепь при


Поскольку переходная характеристика цепи определяется при нулевых независимых начальных условиях:


Составим при
 систему уравнений для определения
систему уравнений для определения
 :
:

Решив которую получим:

Тогда уравнение
для


Выражение переходной
характеристики
 выходной реакции:
выходной реакции:

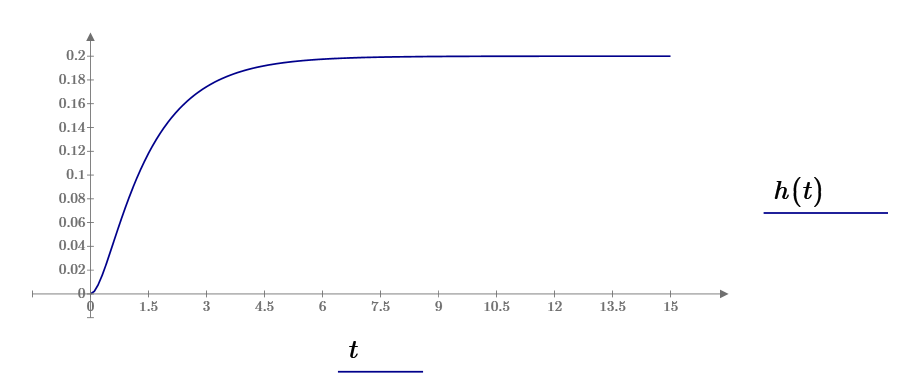
Рис.7. Переходная характеристика реакции
АНАЛИЗ ЦЕПИ ОПЕРАТОРНЫМ МЕТОДОМ ПРИ ДЕЙСТВИИ ОДИНОЧНОГО ИМПУЛЬСА НА ВХОДЕ.
Исходные данные:
В момент времени
 на вход цепи на рис. 1 при нулевых
независимых начальных условиях подается
сигнал в виде одиночного импульса
на вход цепи на рис. 1 при нулевых
независимых начальных условиях подается
сигнал в виде одиночного импульса
 ,
заданного графиком (рис. 8) с параметрами:
,
заданного графиком (рис. 8) с параметрами:




Рис. 8. Исходный импульс
Определение функции передачи цепи.

где
 ,
,
 - изображения по Лапласу реакции и
воздействия.
- изображения по Лапласу реакции и
воздействия.
Операторная схема замещения цепи:
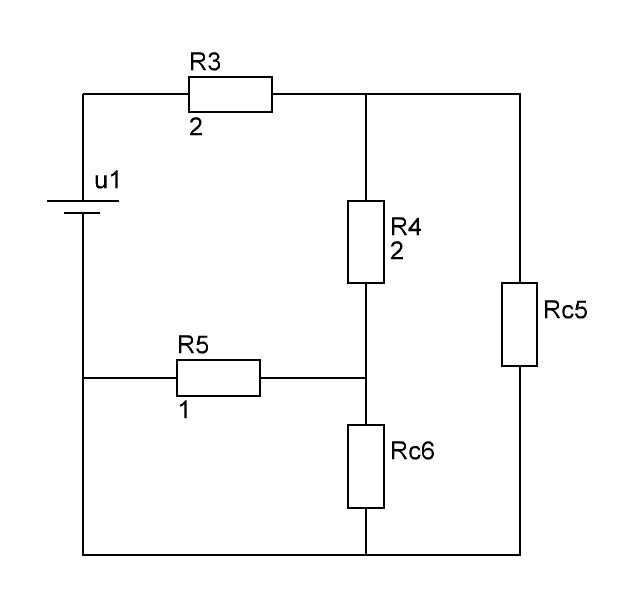
Рис. 9. Операторная схема замещения
Здесь
 ,
,


Применим метод контурных токов:



Найдем определитель:

Определитель для первого контура:

Определитель для третьего контура:

Найдем контурные токи:


Ток на
 :
:



Определим
значения
 при
при


Рис. 10. Схемы
замещения при а –
 ;
б –
;
б –

Определение нулей и полюсов функции передачи
Нули – корни
числителя, полюсы – корни полинома
знаменателя функции передачи. Конечных
нулей функция передачи
не имеет. Полюсы, называемые также
частотами собственных колебаний цепи,
являются согласно корнями характеристического
уравнения
 .
Они равны:
.
Они равны:
 ,
,
 .
Расположение полюсов на плоскости
комплексной частоты приведено на рис.
11.
.
Расположение полюсов на плоскости
комплексной частоты приведено на рис.
11.
Исходя из вида полюсов (отрицательные, комплексно-сопряженные) можно сделать вывод, что переходный процесс носит колебательный затухающий характер.

Рис. 11. Полюса функции
Определение переходной характеристики цепи.
Переходную
характеристику
– реакцию цепи на единичную ступенчатую
функцию
при нулевых независимых начальных
условиях – находим как оригинал функции



Проверим найденные
значения по схемам замещения исходной
цепи, соответствующим
(рис.
11, б),
где
 ,
и
,
и
 (рис. 11, а),
где
(рис. 11, а),
где
 ;
из схемы на рис 11, а
имеем
;
из схемы на рис 11, а
имеем
 ,2,
на рис 11, б
имеем
,2,
на рис 11, б
имеем
 .
.
Определение изображения по Лапласу входного одиночного импульса
Входной одиночный импульс напряжения приведенный на рис. 8, описывается следующей функцией:

Используя теорему смещения в вещественной области, получим:

Определение изображения выходного сигнала
 и реакции
цепи во всей временной области
и реакции
цепи во всей временной области
 .
.
Изображение выходного напряжения:

Оригинал
 находим, используя теорему смещения в
вещественной области. Выходное напряжение:
находим, используя теорему смещения в
вещественной области. Выходное напряжение:


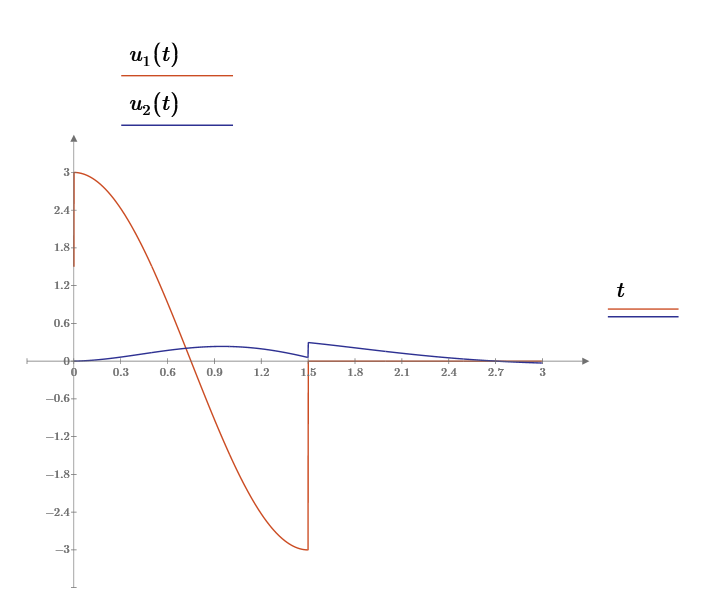
Рис. 12. Графики
входного
 и выходного
и выходного
 сигналов.
сигналов.
АНАЛИЗ ЦЕПИ ЧАСТОТНЫМ МЕТОДОМ ПРИ ДЕЙСТВИИ ОДИНОЧНОГО ИМПУЛЬСА НА ВХОДЕ
Определение амплитудно-частотной и фазочастотной характеристик цепи
Обобщенная частотная
характеристика цепи
 ,
т.е. амплитудно-фазовая характеристика,
определяет связь реакции и воздействия
в установившимся синусоидальном режиме
для любой частоты:
,
т.е. амплитудно-фазовая характеристика,
определяет связь реакции и воздействия
в установившимся синусоидальном режиме
для любой частоты:

тогда амплитудно-частотная характеристика

фазочастотная характеристикаг

Из выражения АЧХ
имеем
 и
и
 .
.
Графики АЧХ (рис. 13) и ФЧХ (рис. 14) функции передачи цепи.
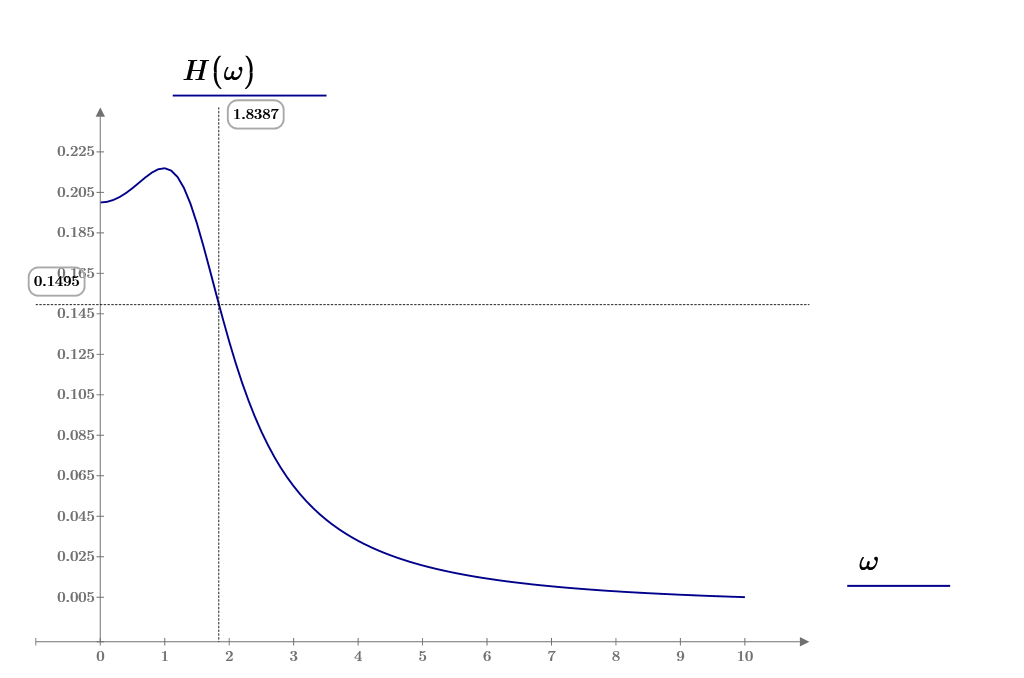
Рис. 13. График АЧХ
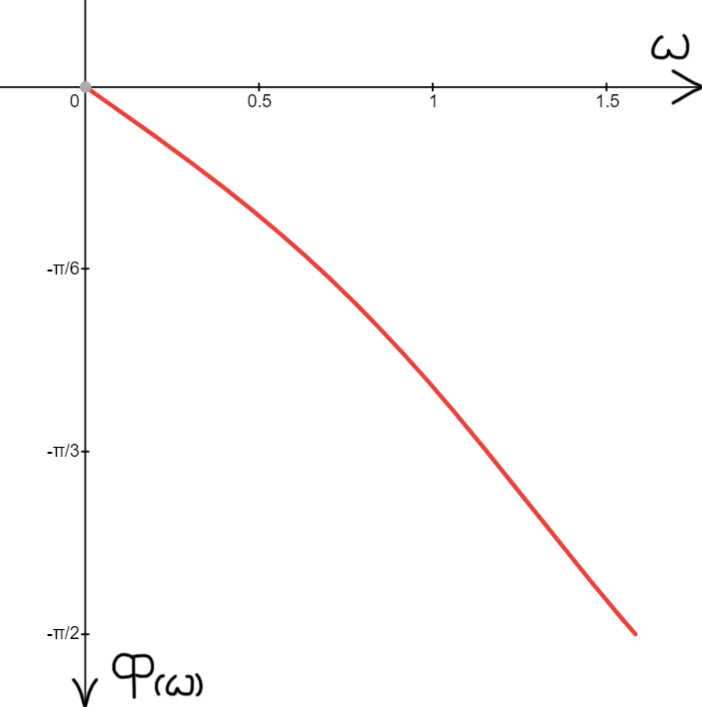
Рис. 14. График ФЧХ
Определение полосы пропускания цепи
Полоса пропускания цепи:


Полоса пропускания,
найденная по графику
 на рис. 13, составляет:
на рис. 13, составляет:

Вывод
Сравнивая входной и выходной сигналы цепи сделан вывод, что схема представляет собой фильтр верхних и низких частот.
Санкт-Петербург
2022
