пиво №12

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Техническая электродинамика и антенны»

Лабораторная работа №12

«Измерение сопротивления нагрузки и настройка волноводной линии в режим бегущей волны»

Выполнил: студент гр. БИН2104 Зайцева О.С.

Проверил:

Москва, 2023 г.

Цель работы

1. Ознакомление с методикой измерения эквивалентных сопротивлений волновода по найденному распределению поля в волноводе.

2. Приобретение навыков пользования круговой диаграммой полных сопротивлений.

3. Ознакомление с методикой настройки волноводов на бегущую волну путем включения неоднородности.

Блок-схема лабораторной установки

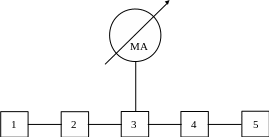
Рис.1.

1 - генератор СВЧ колебаний, работающий в диапазоне 30....37,5 ГГц;

2 - возбудитель волны типа (коаксиально-волноводный переход);

3 - измерительная линия; 4 - согласующая секция; 5 — нагрузка.

Домашний расчёт

1. Исходные данные

- коэффициент бегущей волны задаётся одинаковым для обеих задач.

Для задачи № 1:

- нормированное расстояние, являющееся отношением длины рассматриваемого участка линии к длине волны в линии. Его значение в сочетании с известным однозначно определяет на диаграмме полных сопротивлений точку, соответствующую нормированному значению сопротивления нагрузки .

Направление смещения: к генератору. Нормированное расстояния до точки, определяющей ведётся в направлении, противоположном заданному направлению смещения.

Для задачи № 2:

; Направление смещения: к нагрузке.

2. Расчёт сопротивления нагрузок и соответствующих им входных сопротивлений линий с помощью круговой диаграммы

Требуется рассчитать входные сопротивления линии передачи (волновода) для двух сопротивлений нагрузки (первое сопротивление задано в задаче №1, второе - в задаче № 2) при изменении длины линии от значения до значения с шагом , где m – некоторое целое положительное число, а Λ - длина волны в линии. Таким образом, поставлена задача: проследить характер изменения значений входного сопротивления при изменении длины линии в рамках одного периода ( ). Начальная точка, направление смещения и коэффициент бегущей волны приведены в исходных данных, поэтому задача сводится к серии графических построений на диаграмме полных сопротивлений.

Для начала необходимо провести прямую, соединяющую точку с заданным нормированным расстоянием, причём данное расстояние откладывается противоположно указанному направлению смещения ( получаем к нагрузке) и центр диаграммы (точку r = 1). Пересечение этой прямой с окружностью (нанесена на диаграмму пунктиром) даёт нам точку А, которая определяет нормированное значение полного сопротивления нагрузки. Теперь, чтобы получить первое значение входного сопротивления, необходимо сдвинуться от полученной точки A на относительных единиц по направлению к генератору, получив таким образом отметку относительного расстояния по внутренней окружности. Затем полученная отметка соединяется с центром диаграммы, точка пересечения соединяющей прямой с окружностью , назовём её B, будет определять первое значение входного сопротивления линии. Далее происходит очередное смещение на , аналогичным образом определяет точка С и т .д. Ход построений проиллюстрирован на рис.1. Таким способом определяем входные сопротивления при изменении нормированного расстояния с шагом 0,01 до тех пор, пока не будет пройден полный период изменения значений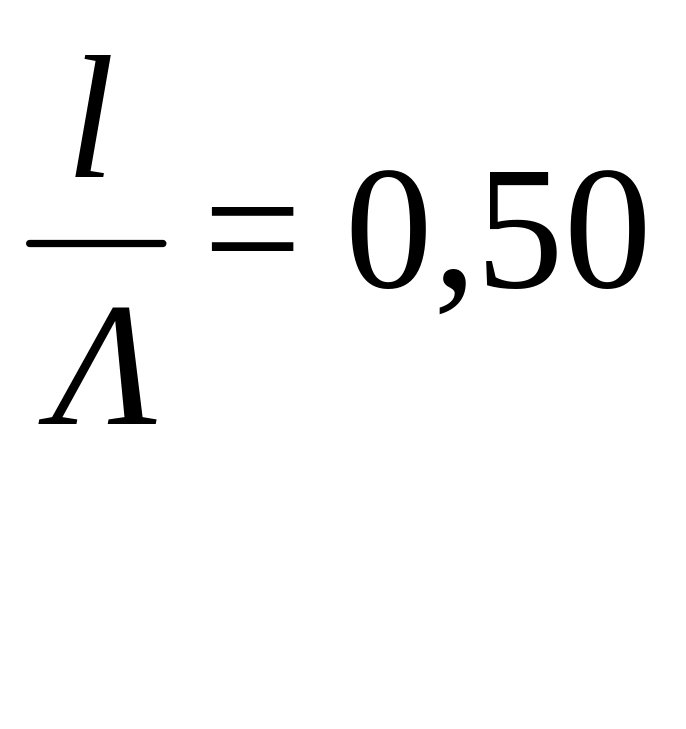 . Данные заносятся в табл.1.

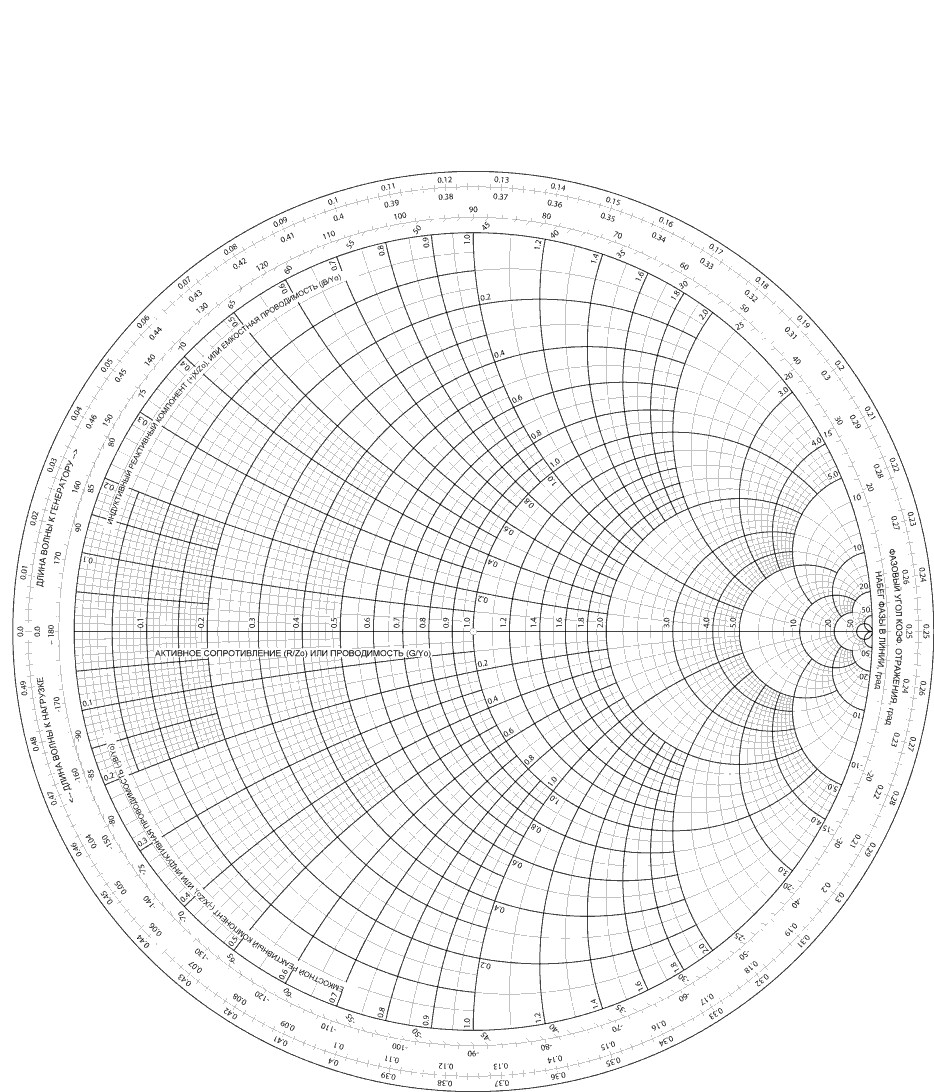
Рис.2. Круговая диаграмма полных сопротивлений для задачи № 1.

Табл.1. Входные сопротивления, определённые для задачи № 1,

, ед.	0,02	0,07	0,12	0,17	0,22
, eд.	0,3+i0,12	0,36+i0,44	0,51+i0,9	0,98+i1,76	2,5+i1,3
, ед.	0,27	0,32	0,37	0,42	0,47
, eд.	2,9-i1,2	1,15-i2,2	0,58-i1,05	0,38-i0,54	0,3-i0,19

Для задачи № 2 методика решения и графических построений не изменяется, отличаются только заданная начальная отметка нормированного расстояния и направление смещения, в котором его следует отсчитывать (в данном случае указано смещение к нагрузке, значит необходимо определять начальную точку по внешней окружности, т. е. отсчитывая к генератору). Как и в предыдущей задаче соединяем точку 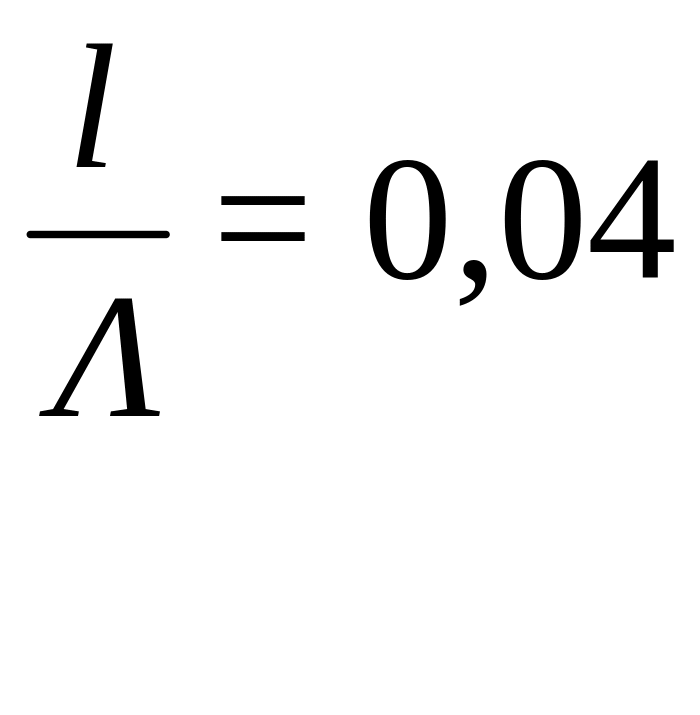относительного расстояния с центром диаграммы и ищем точку пересечения полученной прямой с окружностью , что даёт точку D. Координаты точки D являют собой нормированное полное сопротивление нагрузки, а для получения первого значения входного сопротивления линии необходимо произвести смещение по шкале нормированных расстояний на и снова произвести вышеописанные действия. Получившаяся точка E определяет первое значение входного сопротивления линии, аналогичным образом строится точка F, определяющая второе значение входного сопротивления линии и т. д. Процесс иллюстрируется на рис.2. Определение значений входного сопротивления линии со смещением по шкале нормированного расстояния с шагом 0,05 продолжается до тех пор, пока не будет пройден полный период изменения данных значений . Данные заносятся в табл.2.

Рис.3. Круговая диаграмма полных сопротивлений к задаче № 2.

Табл.2. Входные сопротивления, определённые для задачи № 2,

, ед.	0,04	0,09	0,14	0,19	0,24
, eд.	0,31-0,23i	-0,58i	-1,18i	-2,4i	-2,6i
, ед.	0,29	0,34	0,39	0,44	0,49
, eд.	+1,4i	+1,56i	+0,76i	+0,35i	+0,7i

7