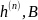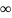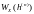Курсовая по ОТС - 2 вариант
.docxФедеральное Агентство Связи Федеральное Государственное Бюджетное Образовательное Учреждение Высшего Образования Ордена Трудового Красного знамени «Московский технический университет связи и информатики»
Кафедра общей теории связи
Курсовая работа по дисциплине
«Общая теория связи»
Вариант № 2
Выполнил: ст. гр. БПЗ1802 Аркадьев Илья Дмитриевич Проверил:
Терехов Алексей Николаевич
Москва 2020
Исходные данные
ИС; АЦП; L=8 |
ПДУ |
НКС |
ПРУ |
Функция
корреляции сообщения
|
||||||
|
|
способ передачи |
частота МГц |
G0, Вт*с |
h02 |
способ приема |
||||
f0 |
f1 |
|||||||||
1.5 |
14 |
ЧМ |
1.1 |
1.25 |
0.0010 |
8.5 |
НП |
|
||
Структурная схема системы электросвязи
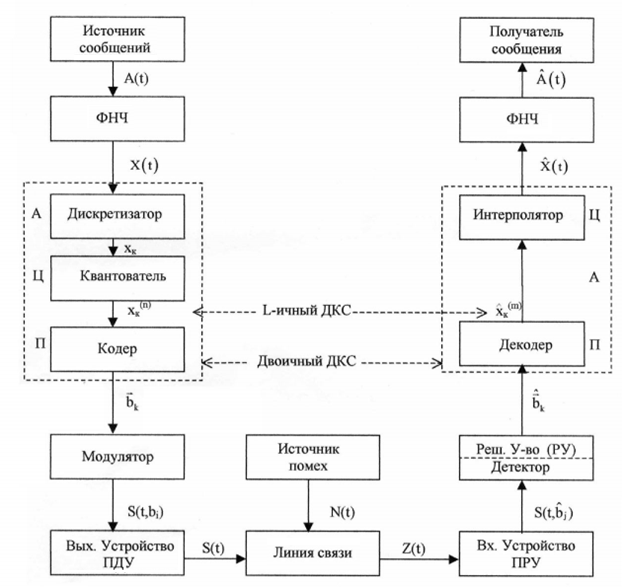
Рисунок 1. Структурная схема системы электросвязи
Источник сообщения –объект или система, информацию от которого необходимо передать.
ФНЧ (фильтр нижних частот) – фильтр, ограничивающий спектр сигнала верхней частотой FВ.
Дискретизатор – представляет отклик ФНЧ в виде последовательности отсчетов xk.
Квантователь
– преобразует отсчёты в квантованные
уровни xk(n);
k=0,
1, 2 …;
 ,
где L
– число уровней квантования.
,
где L
– число уровней квантования.
Кодер – кодирует квантованные уровни двоичным безызбыточным кодом, т.е. формирует последовательность комбинаций ИКМ bk(n).
Модулятор – формирует сигнал, амплитуда, частота или фаза которого изменяются в соответствии с сигналом bk(n).
Выходное устройство ПДУ – осуществляет фильтрацию и усиление модулированного сигнала для предотвращения внеполосных излучений, и обеспечения требуемого соотношения сигнал-шум на входе приемника.
Линия связи – среда или техническое сооружение, по которым сигнал поступает от передатчика к приемнику. В линии связи на сигнал накладывается помеха.
Входное устройство ПРУ – осуществляет фильтрацию принятой смеси – сигнала и помехи.
Детектор
– преобразует принятый сигнал в сигнал
ИКМ
 .
.
Декодер – преобразует кодовые комбинации в импульсы.
Интерполятор и ФНЧ – восстанавливают непрерывный сигнал из импульсов-отсчётов.
Получатель – некоторый объект или система, которому передается информация.
Временные диаграммы
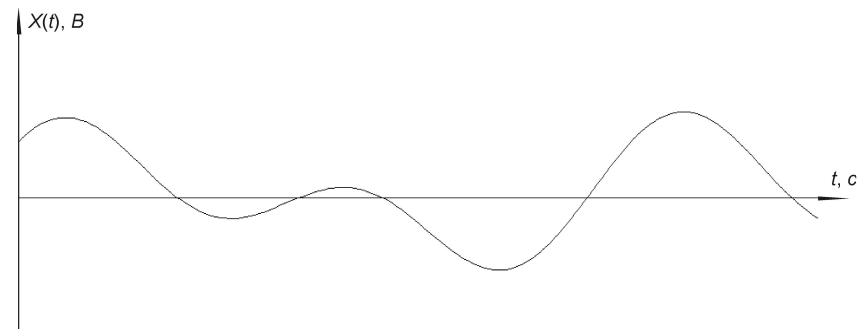
Рисунок 2. Исходное сообщение.
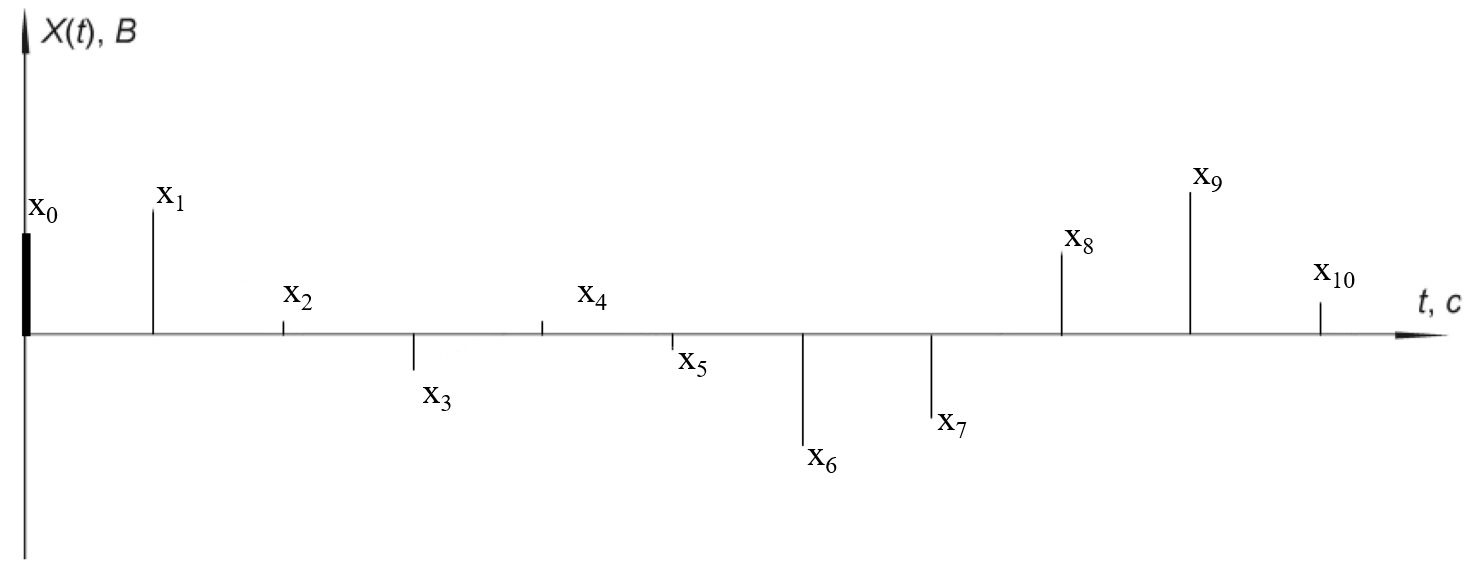
Рисунок 3. Сигнал на выходе дискретизатора
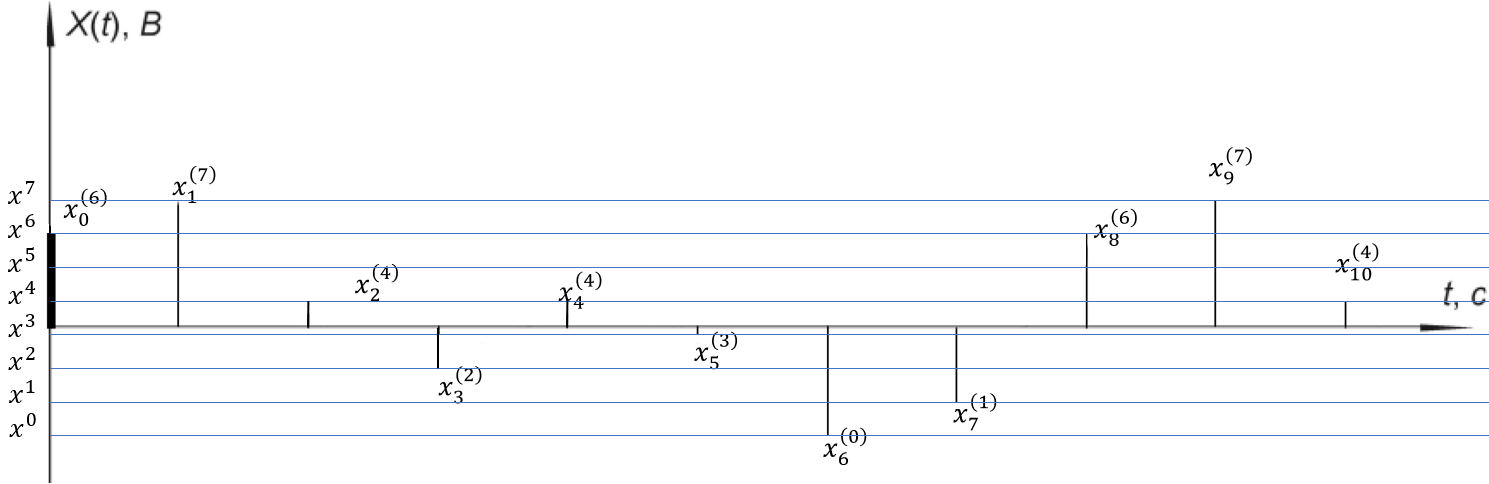
Рисунок 4. Сигнал на выходе квантователя
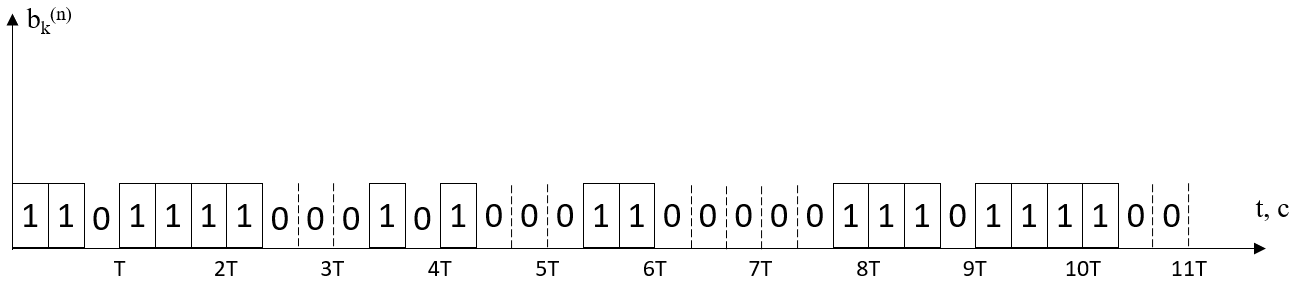
Рисунок 5. Сигнал на выходе кодера.

Рисунок 6. Сигнал на выходе модулятора.
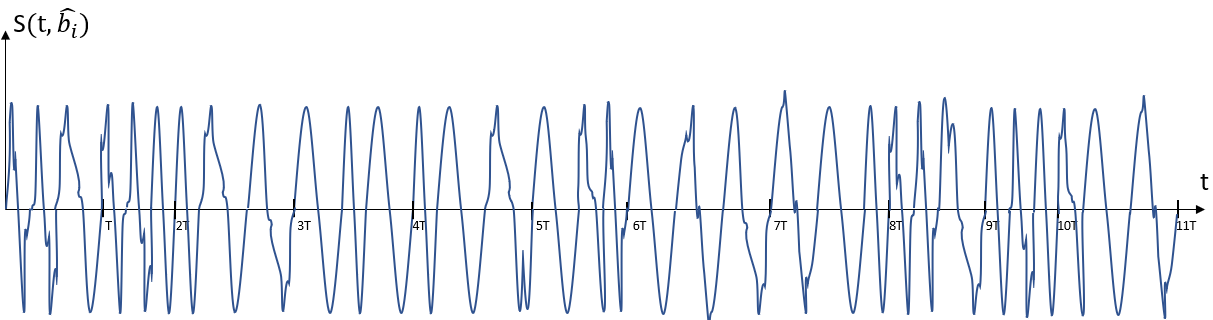
Рисунок 7. Сигнал на входе детектора, пораженный помехой.
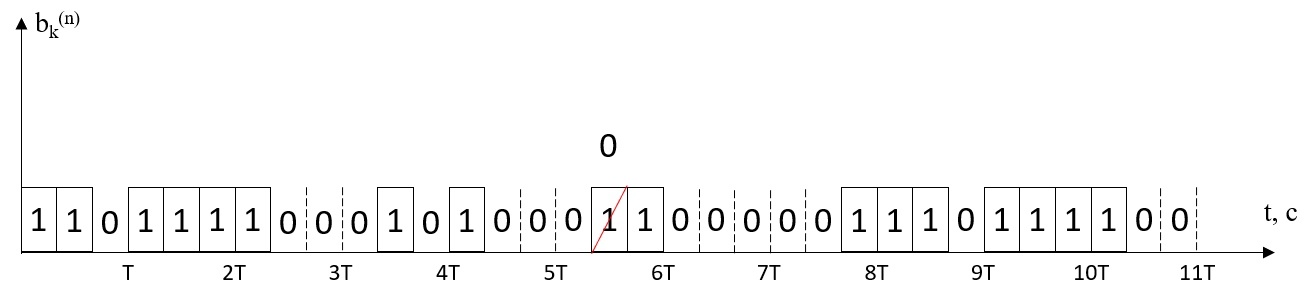
Рисунок 8. Сигнал на выходе решающего устройства.
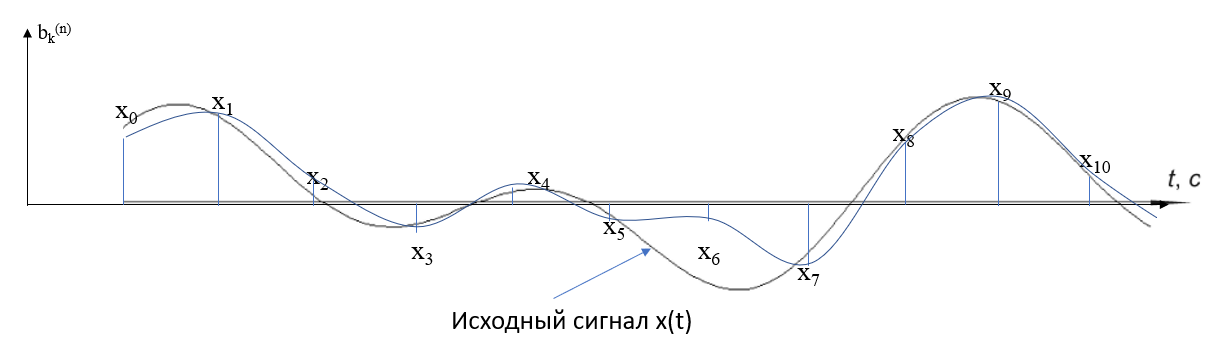
Рисунок 9. Сигнал на выходе декодера.

Рисунок 10. Спектр сигнала на выходе дискретизатора
По заданной функции корреляции исходного сообщения:
Рассчитать интервал корреляции, спектр плотности мощности и начальную энергетическую ширину спектра сообщения:
Рассчитаем интервал корреляции:
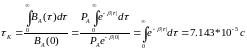
Рассчитаем спектр плотности мощности, воспользовавшись преобразованием Винера - Хинчина:
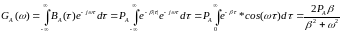
Вычислим начальную энергетическую ширину спектра сообщения

Так
как
 принимает наибольшее значение при
принимает наибольшее значение при
 (первая
производная в этой точке равна 0),
то
(первая
производная в этой точке равна 0),
то

 ,
тогда
,
тогда

Построить в масштабе графики функции корреляции и спектра плотности мощности; отметить на них найденные в пункте а) параметры.
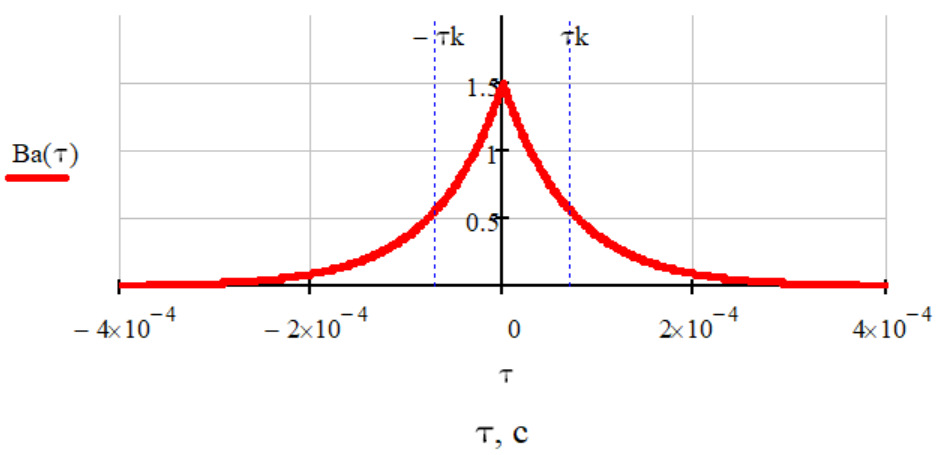
Рисунок 11. График функции корреляции
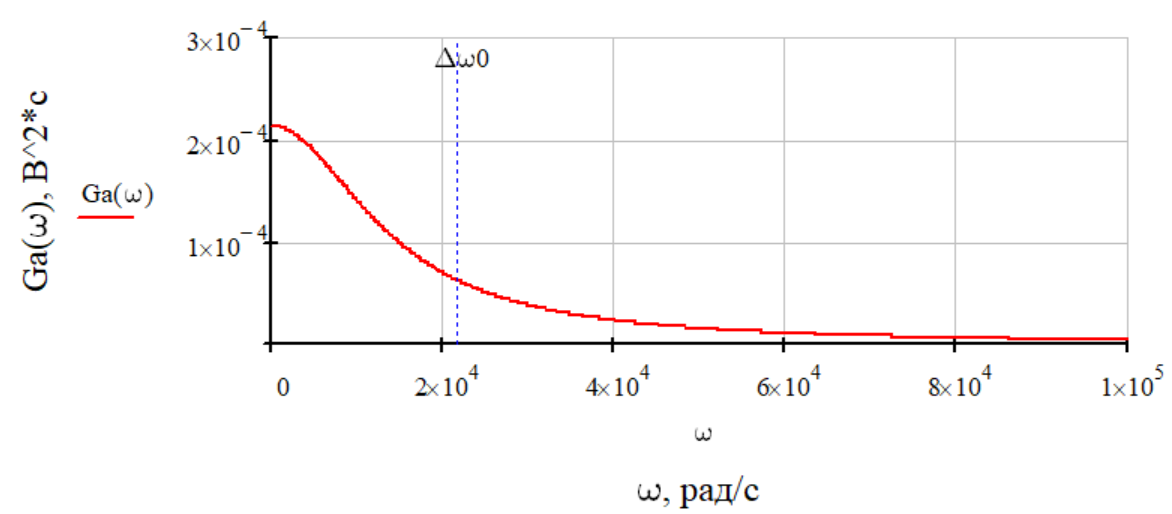
Рисунок 12. График спектра плотности мощности
Считая, что исходное сообщение воздействует на ИФНЧ с единичным коэффициентом передачи и полосой пропускания, равной начальной энергетической ширине спектра сообщения:
Рассчитать СКП фильтрации сообщения, среднюю мощность отклика ИФНЧ, частоту и интервал временной дискретизации отклика ИФНЧ
Вычислим мощность отклика ФНЧ:

Рассчитаем СКП фильтрации:

Найдем частоту и интервал временной дискретизации отклика ИФНЧ:
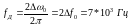
Тогда интервал дискретизации будет равен

Полагая, что последовательность дискретных отсчетов на выходе дискретизатора далее квантуется по уровню с равномерной шкалой квантования:
рассчитать интервал квантования, пороги и уровни квантования, среднюю квадратичную погрешность квантования (СКП);
Рассчитаем шаг квантования:

Определим пороги квантования:

Занесем рассчитанные данные в таблицу:
Таблица 2. Значения порогов квантования
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
-2.937 |
-1.958 |
-0.979 |
0 |
0.979 |
1.958 |
2.937 |
|
Уровни квантования определим по следующим выражениям:
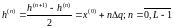

Таблица 3. Значения уровней квантования
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
-3.427 |
-2.448 |
-1.469 |
-0.49 |
0.49 |
1.469 |
2.448 |
3.427 |
Определим среднюю квадратическую погрешность квантования (мощность шума квантования):
Для этого вычислим коэффициент взаимной корреляции между входным и выходным сигналами квантователя:
 ,
где
,
где
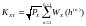
 -
ФПВ гауссовской случайной величины
-
ФПВ гауссовской случайной величины
Таблица 4. Значения гауссовской случайной величины для порогов квантования
|
-2.937 |
-1.958 |
-0.979 |
0 |
0.979 |
1.958 |
2.937 |
|
0.0045 |
0.055 |
0.247 |
0.407 |
0.247 |
0.055 |
0.0045 |
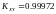 ,
следовательно
,
следовательно
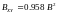
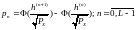
 -
табулированная ф-ция Лапласа
-
табулированная ф-ция Лапласа

Теперь окончательно рассчитаем мощность шума квантования:

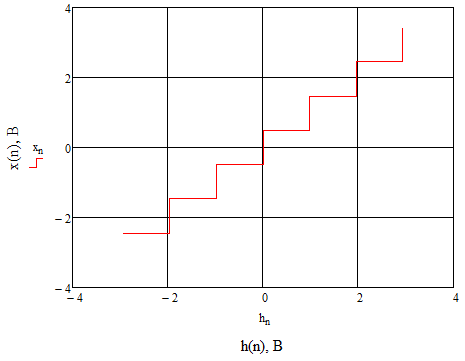
Рисунок 13. Характеристика квантования
Рассматривая отклик квантователя как случайный дискретный сигнал с независимыми значениями на входе L-ичного дискретного канала связи (ДКС):
рассчитать закон и функцию распределения вероятностей квантования сигнала, а также энтропию, производительность и избыточность L-ичного дискретного источника.
Интегральное распределение вероятностей.

Рассчитаем энтропию.
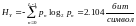
Производительность ДКС определяется соотношением:

Избыточность последовательного источника:

Hmax – максимальная энтропия, для источника дискретных сообщений
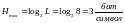
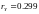

построить в масштабе графики рассчитанных законов и функций распределения вероятностей.

Рисунок 14. График закона распределения вероятности
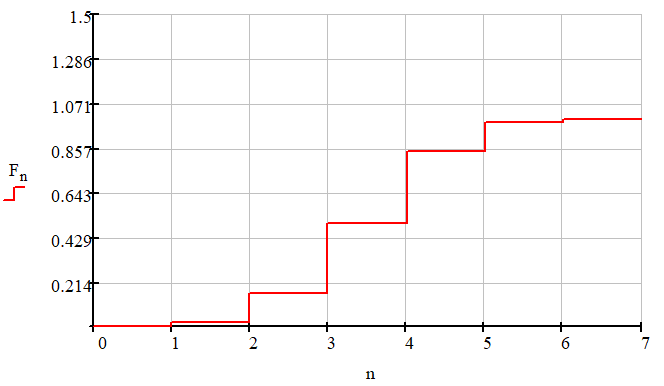
Рисунок 15. График функции распределения вероятностей
Закодировать значения L-ичного дискретного сигнала двоичным блочным примитивным кодом, выписав все кодовые комбинации и построить таблицу кодовых расстояний кода:
Запишем в таблицу все возможные кодовые комбинации:
Таблица 5. Таблица кодовых комбинаций
-

000
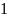
001
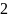
010

011

100

101

110

111
Таким образом, получаем сигнал импульсно-кодовой модуляции (ИКМ)
Построим таблицу кодовых расстояний:
Таблица 6. Таблица кодовых расстояний
|
000 |
001 |
010 |
011 |
100 |
101 |
110 |
111 |
000 |
0 |
1 |
1 |
2 |
1 |
2 |
2 |
3 |
001 |
1 |
0 |
2 |
1 |
2 |
1 |
3 |
2 |
010 |
1 |
2 |
0 |
1 |
2 |
3 |
1 |
2 |
011 |
2 |
1 |
1 |
0 |
3 |
2 |
2 |
1 |
100 |
1 |
2 |
2 |
3 |
0 |
1 |
1 |
2 |
101 |
2 |
1 |
3 |
2 |
1 |
0 |
2 |
1 |
110 |
2 |
3 |
1 |
2 |
1 |
2 |
0 |
1 |
111 |
3 |
2 |
2 |
1 |
2 |
1 |
1 |
0 |
рассчитать априорные вероятности передачи по двоичному ДКС символов нуля и единицы, начальную ширину спектра сигнала ИКМ.
Так как среднее число нулей и единиц в сигнале ИКМ одинаково, то вероятности их появления тоже одинаковы: p (0) = p (1) = 0.5
Ширина спектра сигнала ИКМ равна:
 – постоянная
– постоянная

Полагая, что для передачи ИКМ сигнала по непрерывному каналу связи (НКС) используется гармонический переносчик:
рассчитать нормированные к амплитуде переносчика спектр модулированного сигнала и его начальную ширину спектра:
Сигнал ДЧМ представляется в виде:
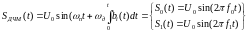
Где ωп – частота переносчика, ωд – девиация частоты.
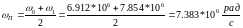

Разложение сигнала в ряд по гармоническим составляющим:
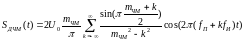
Где
 – индекс частотной модуляции
– индекс частотной модуляции
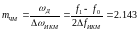
Теперь вычислим ширину спектра ДЧМ:
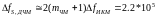
При
неизвестной амплитуде
 вычисляют нормированный спектр
вычисляют нормированный спектр

построить в масштабе график нормированного спектра сигнала дискретной модуляции и отметить на нем найденную ширину спектра:
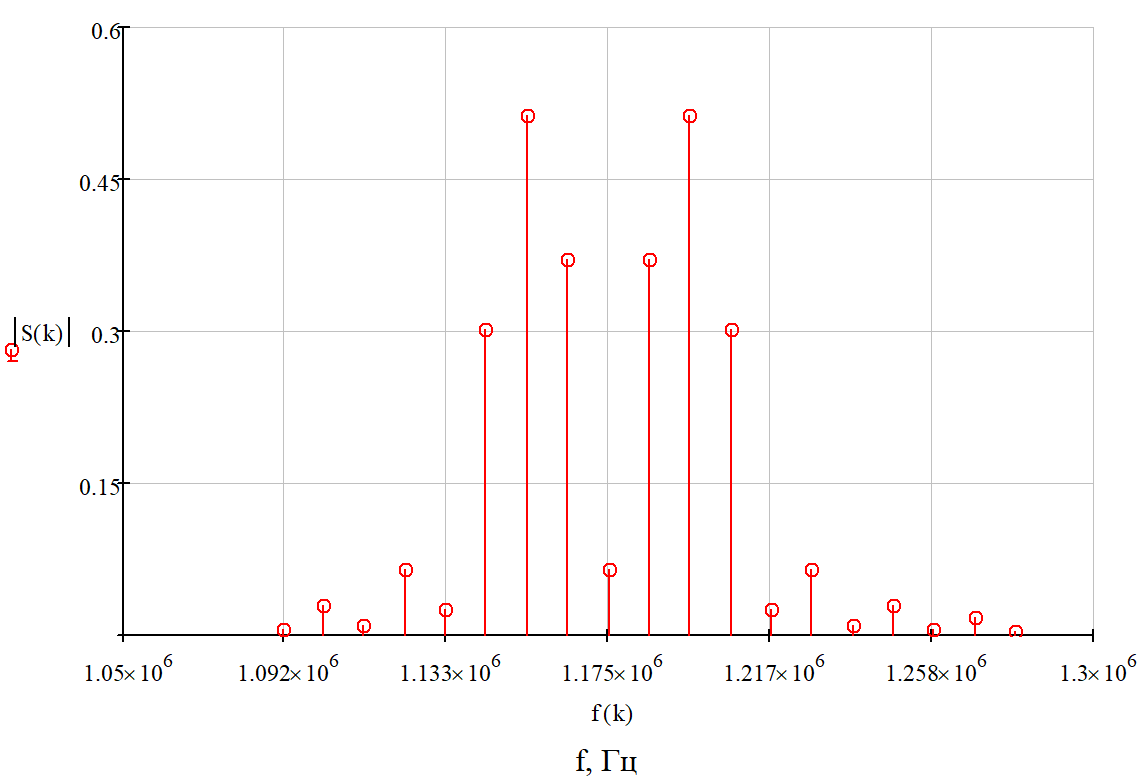
Рисунок 16. График нормированного спектра сигнала дискретной модуляции
Рассматривая НКС как аддитивный гауссовский канал с ограниченной полосой частот, равной ширине спектра сигнала дискретной модуляции, и заданными спектральной плотностью мощности помехи и отношением сигнал-шум:
Рассчитать приходящиеся в среднем на один двоичный символ мощность и амплитуду модулированного сигнала, дисперсию (мощность) аддитивной помехи в полосе частот сигнала, пропускную способность НКС;
Мощность АБГШ в полосе пропускания:

Мощность сигнала, обеспечивающего необходимое соотношение с/ш на входе приёмника

Мощность сигнала ДЧМ и амплитуда, в среднем приходящиеся на один двоичный символ:

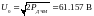
Пропускная способность гауссовского НКС:

Построить в масштабе четыре графика плотности вероятностей (ФПВ) мгновенных значений и огибающих узкополосной гауссовской помехи (УГП) и суммы гармонического сигнала с УГП.
ФПВ мгновенных значений УГП
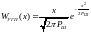
ФПВ мгновенных значений принятого сигнала имеет вид:


Рисунок 17. Графики ФПВ мгновенных значений гауссовской помехи и помехи + гармонического сигнала
Огибающая гауссовской помехи распределена по закону Релея, т.е.

ФПВ огибающей гауссовской помехи + гармонического сигнала распределена по обобщённому закону Релея:
 ,
где
,
где
I0 – модифицированная функция Бесселя нулевого порядка от мнимого аргумента
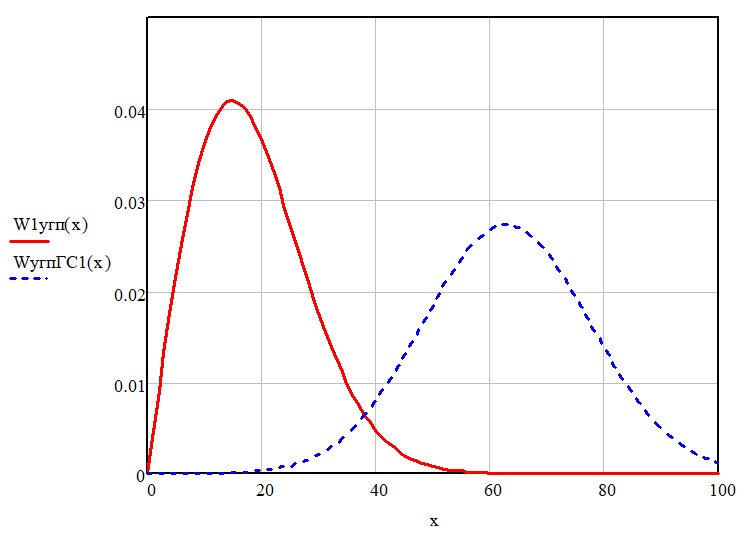
Рисунок 18. Графики ФПВ огибающей гауссовской помехи, гауссовской помехи + гармонического сигнала
С учетом заданного вида приема (детектирования) сигнала дискретной модуляции:
Рассчитать среднюю вероятность ошибки в двоичном ДКС, скорость передачи информации по двоичному симметричному ДКС, показатель эффективности передачи сигнала дискретной модуляции по НКС;
Средняя вероятность ошибки в двоичном ДКС:

При
равенствах априорных вероятностей
p(0)=p(1)=0,5,
а также условных вероятностей (условие симметричности двоичного ДКС),
средняя на бит вероятность ошибки равна
(условие симметричности двоичного ДКС),
средняя на бит вероятность ошибки равна
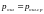
При некогерентном приеме ДЧМ:


Скорость передачи информации по двоичному симметричному ДКС, когда определяется:

Так
как вероятность
 для различных видов сигналов зависят
от
для различных видов сигналов зависят
от
 на входе детектора, то и
на входе детектора, то и
 зависит от ОСШ. Для сравнения скорости
зависит от ОСШ. Для сравнения скорости
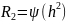 при данном виде модуляции и способе
приема с пропускной способностью НКС
при данном виде модуляции и способе
приема с пропускной способностью НКС
 вводят
показатель эффективности:
вводят
показатель эффективности:

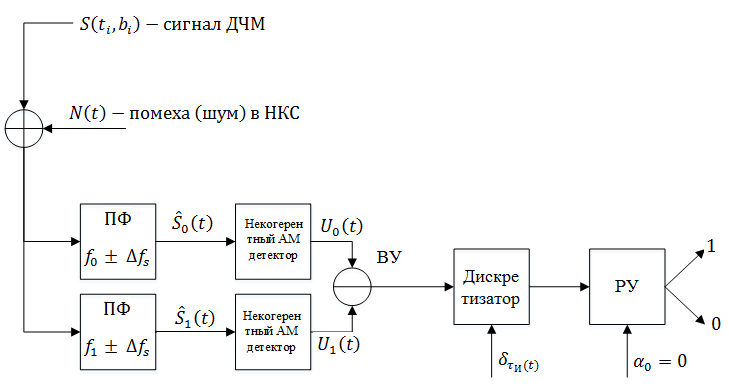
Рисунок 19. Приемник сигналов ДЧМ
Сигнал, проходящий по каналу связи, подвергается воздействию помех. На входе приемника стоит два полосовых фильтра, настроенных на частоты f0 и f1, соответствующие передаче логического «0» и «1». Далее, принятый сигнал поступает на вход некогерентного детектора АМ (состоящий из диода и фильтра-интерполятора – RC цепи). При передаче «1» ПФ, настроенный на частоту f0, примет лишь шум из полосы пропускания и на оборот. При подаче сигналов с двух амплитудных детекторов, ВУ вычитает сигнал одного канала из сигнала другого и при положительном результате РУ выдает «1». Ошибочное решение будет принято, если уровень шума на выходе канала без сигнала будет выше, чем уровень с сигналом.
Рассматривая отклик декодера ПРУ как случайный дискретный сигнал на входе L – ичного ДКС:
Рассчитать распределение вероятностей дискретного сигнала на выходе декодера, скорость передачи информации по L – ичному ДКС, относительные потери в скорости передачи информации по L – ичному ДКС:
Распределение вероятностей дискретного сигнала на выходе детектора определяется выражением:

где
 –
вероятность ошибки в двоичном симметричном
ДКС;
–
вероятность ошибки в двоичном симметричном
ДКС;
 –
вероятность
правильного приема двоичного символа,
–
вероятность
правильного приема двоичного символа,
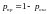
Таблица 7. Таблица распределения вероятностей дискретного сигнала на выходе детектора
m |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
0.00485 |
0.02433 |
0.1356 |
0,33522 |
0,33522 |
0.1356 |
0.02433 |
0.00485 |
Для
определения скорости передачи информации
 по L-ичному
ДКС воспользуемся соотношением:
по L-ичному
ДКС воспользуемся соотношением:


 -
энтропия восстановленного L-ичного
сообщения
-
энтропия восстановленного L-ичного
сообщения

Зная скорость ввода информации в ДКС и скорость передаваемой по ДКС информации находим величину относительных потерь в скорости:


 ,
В2
,
В2 ,
с-1
,
с-1 ,
,