laba_14

«Московский Технический Университет Связи и Информатики»

Кафедра теории электрических цепей

Лабораторная работа № 14

по ОКАЭЦ

«Исследование КИХ-фильтров»

Выполнил: ст. БИН2104 Зайцева О.С.

Проверил: Микиртичан А.Г.

Вопросы для самопроверки:

1. Что называется Z-преобразованием?

Переход от оригинала 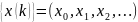к изображению определяемый равенством:

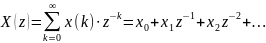
называется z-преобразованием.

2. Какими свойствами обладает Z-преобразование?

Свойство 1. Линейность. Z-образ суммы двух сигналов равен сумме z-образов этих сигналов. Действительно, пусть есть два дискретных сигнала   и  , . Найдем z-преобразование их суммы :

(11)

Свойство 2. Свойство задержки. Пусть дан исходный дискретный сигнал  ,  . Найдем z-преобразование сигнала  , задержанного на   отсчетов:

(12)

При выводе была введена переменная  , тогда   и получили, что задержка исходного сигнала на  добавляет множитель   к z-преобразованию сигнала. Тогда задержка на один отсчет соответствует  .

Свойство 3. Теорема о свертке. Пусть дано два сигнала   и  , . Найдем z-преобразование их круговой свертки.

(13)

При выводе было использовано свойство задержки z-преобразования. Таким образом z-преобразование свертки сигналов равно произведению их z-образов.

3. Какие фильтры называются цифровыми?

Цифровой фильтр – это устройство которое преобразует последовательность числовых отсчетов 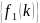входного сигнала в последовательность отсчетов выходного сигнала.

Цифровой фильтр

4. Дайте определение передаточной функции цифрового фильтра?

Передаточной функцией стандартного линейного ЦФ называется отношение z-преобразования выходного сигнала к Z-преобразованию входного сигнала.

Цифровой фильтр

5. Какие фильтры называются КИХ-фильтрами?

Фильтром с конечной импульсной характеристикой (КИХ-фильтром) называется фильтр, у которого импульсная характеристика представляет собой конечную дискретную последовательность, т. е. принимает отличные от нуля значения при k= 0, 1, …, m.

Цель работы:

С помощью программы Micro-Cap получить основные временные и частотные характеристики фильтров с конечной импульсной характеристикой (КИХ-фильтров).

Предварительный расчёт

1. Найти передаточную функцию H(z) трехзвенного КИХ-фильтра второго порядка, выполняющего функцию скользящего среднего.

,

Тогда передаточная функция имеет вид:

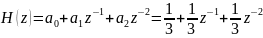
2. Найти выражение для комплексного коэффициента передачи H(jωT). Построить графики АЧХ – |H(jωT)| и ФЧХ – arg(H(jωT)) от частоты ωT ϵ [0, 2π] (T = const – интервал дискретизации по времени) данного фильтра.

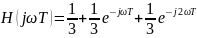
|H(jωT)|

АЧХ:

ωT

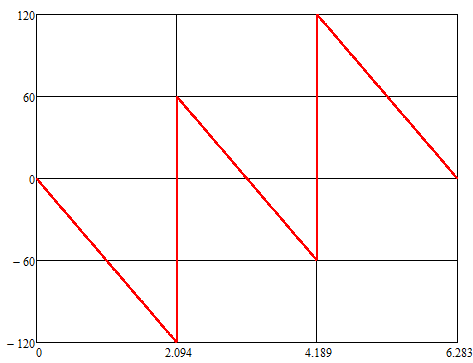
arg(H(jωT))

ФЧХ:

ωT

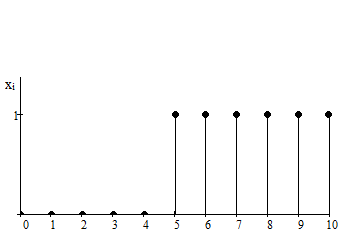3. П олучить реакцию данного КИХ-фильтра на ступенчатое воздействие. Построить график y_i. Получить импульсную характеристику данного фильтра и построить её график.

График y_i:

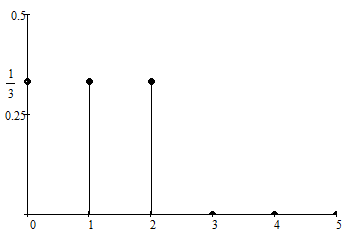
Импульсная характеристика будет иметь вид:

Определяется из коэффициентов передаточной функции H(z)

График импульсной характеристики g(iT):

4. Нарисовать структурную схему четырехзвенного КИХ-фильтра, выполняющего функцию скользящего среднего. Найти его передаточную функцию H(z). Построить графики АЧХ и ФЧХ данного фильтра.

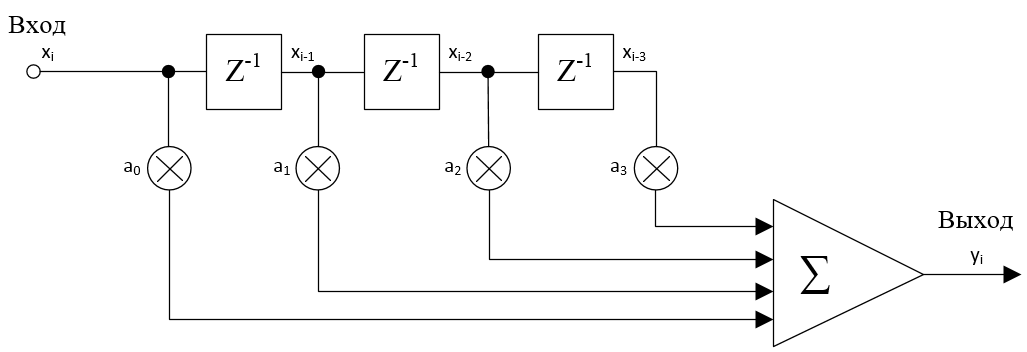
Передаточная функция:

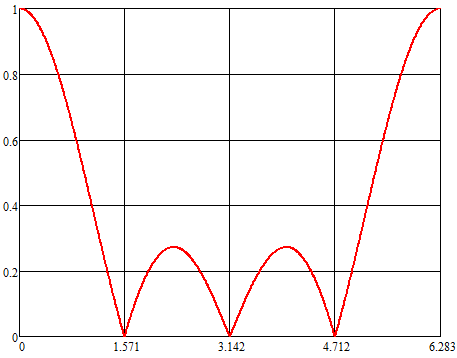
|H(jωT)|

АЧХ:

ωT

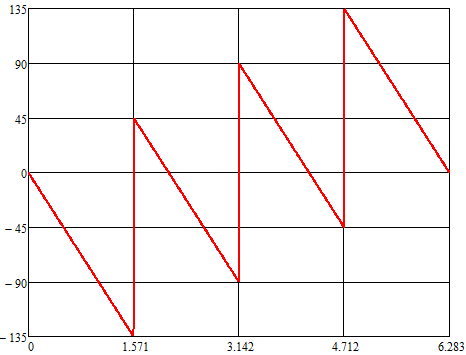
arg(H(jωT))

ФЧХ:

ωT

5. Нарисовать структурную схему пятизвенного КИХ-фильтра, выполняющего функцию скользящего среднего. Найти его передаточную функцию H(z). Построить графики АЧХ и ФЧХ данного фильтра.

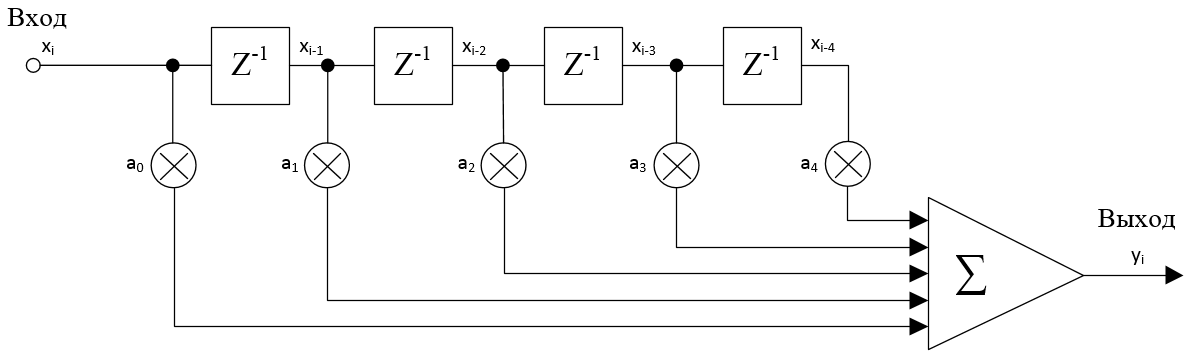
Передаточная функция:

|H(jωT)|

ωT

А ЧХ:

arg(H(jωT))

ФЧХ:

ωT

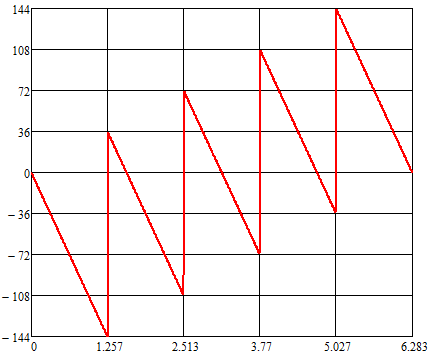
Обработка результатов машинного эксперимента

Схема в Micro-Cap:

ФЧХ трёхзвенного КИХ-фильтра

АЧХ трёхзвенного КИХ-фильтра

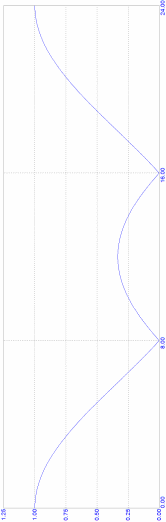
АЧХ четырёхзвенного КИХ-фильтра

ФЧХ четырёхзвенного КИХ-фильтра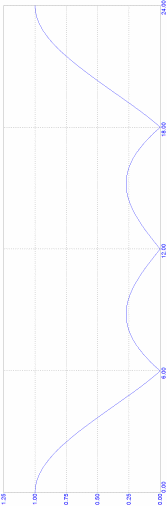

АЧХ пятизвенного КИХ-фильтра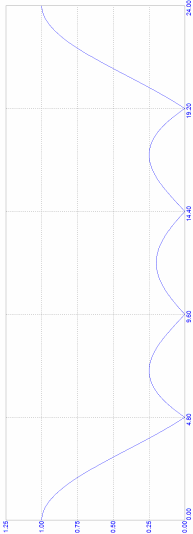

Вывод:

Получены передаточные функции, частотные характеристики и графики АЧХ и ФЧХ КИХ – фильтров второго, третьего и четвертого порядков. Результаты предварительного расчета совпали с результатами компьютерного моделирования.