лаба7

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ, СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

Ордена Трудового Красного Знамени федеральное государственное бюджетное образовательное учреждение высшего образования

«Московский технический университет связи и информатики»

Кафедра «Информатика»

Лабораторная работа №7-1

«Разработка проекта, решающего задачу принадлежности или непринадлежности точки с заданными координатами геометрической фигуре»

по теме:

«Основные понятия алгебры логики. Логические данные, выражения и

операторы VС++ для программной реализации разветвляющихся алгоритмов»

по дисциплине

«Информатика»

Выполнил: студент гр. БИН2104 Зайцева О.С.

С/б №16ИН21092

Вариант 9

Проверил:

Москва, 2021 г.

Содержание

1. Индивидуальное задание 3

2. Формализация задания 3

3. Схема алгоритмов проекта 4-5

4. Программный код проекта 6-7

5. Результаты выполнения проектов 7-8

6. Доказательство правильности работы программы для каждой ветви разветвления 8

Вариант 9

1. Индивидуальное задание

Создать программный проект, решающий задачу-попадает ли точка с координатами (x, y) в круг без треугольника, заданному координатами своих вершин (0, -1), (-1, 0) и (1, 0).

2. Формализация и уточнение задания

Построены «вручную» описанная в постановке задаче фигура, которая определяет область попадания точки в заданную геометрическую фигуру (рисунок 1).

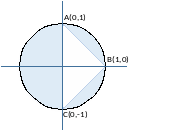
Рисунок 1 – Круг без треугольника, заданным координатами своих вершин

Радиус описанной окружности вокруг треугольника равен 1. Определим уравнения прямых AB, BC и AC, которые ограничивают заданная область:

AB: x + y = 1

BC: x – y = 1 AC: x>0 && |y| <= 1

Требуется вместо уравнений записать неравенства, выполнение которых необходимо для исключения попадания в эту область. Так же нужно определить область попадания точки в круге. В нашем примере все эти неравенства должны выполняться одновременно, поэтому записаны в виде системы 5-ти неравенств, которую можно записать равнозначной системой из 6-и неравенств.

Таким образом, для того, чтобы точка с координатами x, y принадлежала построенному кругу без треугольника, необходимо выполнение следующих условий:

При этом логическое выражение можно записать следующим образом:

= (pow(x, 2.0) + pow(y, 2.0) <= 1) != ((x - y) <= 1 && (x + y) <= 1 &&

x >= 0 && fabs(y) <= 1)

3. Схема алгоритмов проекта

Разработаны схемы 3-х алгоритмов:

• Схема алгоритма reshenie1 решение задачи, использующая стандартное разветвление и сложное логическое выражение (рисунок 2)

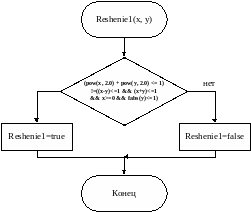
Рисунок 2 – Схема алгоритма функции, использующей стандартное разветвление и сложное логическое выражение

• Схема алгоритма reshenie2 решение задачи, использующая вложенные разветвления только с помощью операций отношения, без использования логических операций и сложных логических выражений (рисунок 3)

Рисунок 3- Схема алгоритма функции, реализующей вложенные разветвления только с помощью операций отношения, без использования логических операций и сложных логических выражений

• Схема алгоритма reshenie3 решение задачи, использующая только сложное логические выражения (рисунок 4)

Рисунок 4 – Схема функционального алгоритма reshenie3, использующая только сложное логическое выражение

4. Программный код проекта

Разработан программный код проекта.

// Файл getput.cpp

#include <iostream>

using namespace std;

// Определение функции ввода

void get_xy(float& x, float& y)

{

setlocale(LC_ALL, "rus");

cout << "Введите координаты точки x, y:\n";

cin >> x >> y;

}

// Определение функции вывода

void put(bool b, float x, float y)

{

setlocale(LC_ALL, "rus");

cout << "Точки с координатами (" << x << ", " << y << ")" << endl;

if (b) cout << "попала в заданную область" << endl;

else cout << "не попала в заданную область" << endl;

}

// Файл с функциями решения задачи, реализующие функциональные // алгоритмы

#include <cmath>

//1-ое решение - стандартное разветвление с логическими операциями

bool reshenie1(float x, float y)

{

if ((pow(x, 2.0) + pow(y, 2.0) <= 1) != ((x-y)<=1 && (x+y)<=1 && x>=0 && fabs(y)<=1))

return true;

else return false;

}

//2-ое решение - вложенные разветвления только с помощью операций отношений

bool reshenie2(float x, float y)

{

if (x * x + y * y <= 1)

if (!((x - y) <= 1 && (x + y) <= 1 && x >= 0 && fabs(y) <= 1)) return true;

return false;

}

//3-е решение - только сложное логические выражения

bool reshenie3(float x, float y)

{

return ((pow(x, 2.0) + pow(y, 2.0) <= 1) != ((x - y) <= 1 && (x + y) <= 1 && x >= 0 && fabs(y) <= 1));

}

// Файл main.cpp

#include <iostream>

using namespace std;

void get_xy(float& x, float& y);

void put(bool, float, float);

bool reshenie1(float x, float y);

bool reshenie2(float x, float y);

bool reshenie3(float x, float y);

int main()

{

float x, y;

bool b, c; //Признак попадания в заданную область

get_xy(x, y); // Вызов функции ввода исходных данных

cout << "\n Решение 1-й функции:" << endl;

b = reshenie1(x, y); // Вызов 1-й функции решения

put(b, x, y); // Вызов функции вывода результатов

cout << "\n Решение 2-й функции: " << endl;

c = reshenie2(x, y); // Вызов 2-й функции решения

put(c, x, y);

cout << "\n Решение 3-й функции: " << endl;

c = reshenie3(x, y); // Вызов 3-й функции решения

put(c, x, y);

system("Pause");

return 0;

}

Программный код проекта

5. Выполнение разработанного проекта.

Получены результаты выполнения проекта, приведенные на рисунках 6-8, для текстовых данных точек, попадающих и не попадающих в заданную область.

Рисунок 6 – Результаты выполнения проекта для тестовых данных точки, попадающей в заданную плоскость

Рисунок 7 – Результаты выполнения проекта для тестовых данных точки, не попадающей в заданную область

6. Доказательство правильности результата

Разработаны тестовые исходные данные для контрольного решения, проверяющие попадание и непопадание точки с различными координатами в заданную область, и получены результаты:

Исходные данные		Результат
x = 0.5	y= 0.8	Точка попала в область
x = 0.4	y = 0.5	Точка не попала в область
x = -0.8	y = -0.7	Точка не попала в область

При тестовых данных результаты ручного расчёта и вычисления на компьютере совпадают.