
Лекции_Теория / Статистическая физика / Глава С3
.pdf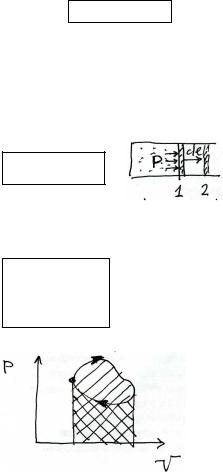
Раздел VI. СТАТИСТИЧЕСКАЯ ФИЗИКА.
Глава 3. Основные законы термодинамики.
1. Первое начало термодинамики.
Q U A
∆Q – тепло, сообщаемое системе.
∆U = U2-U1 - приращение внутренней энергии ∆A – работа, совершаемая системой над внешними телами.
а) Работа, совершаемая газом при изменении объема:
dA pdV
(dA = Fdl = pSdl = pdV)
V2
А12 pdV
V1
Работа при круговом процессе равна площади охватываемой кривой P(V) с точностью до знака.
При движении по часовой стрелке +, против -.
б) Внутренняя энергия идеального газа.
U |
i |
NkT |
i |
|
M |
RT |
N – число молекул. |
|
|
|
|||||
2 |
|
2 |
|
||||
|
|
|
|
|
|
|
M – масса газа. |
|
|
|
|
|
|
|
µ - масса моля. |
i =iпост iвращ 2iкол
в) Теплота, теплоемкость. |
|
||||||
Теплоемкость тела |
C |
dQ |
|
[ |
Дж |
] |
|
dT |
K |
||||||
|
|
|
|
||||
dQ – теплота, сообщенная телу |
|
||||||
dT – соответствующее изменение температуры.
Удельная теплоемкость |
c |
C |
|
[ |
|
Дж |
] |
|
|||
|
|
|
M |
|
K кг |
||||||
|
|
|
|
[ |
Дж |
] |
|||||
Молярная теплоемкость |
C |
c |
|
||||||||
|
|||||||||||
|
|
|
|
|
|
|
|
K моль |
|||
|
|
|
|
|
|
|
|||||
dQ cMdT C M dT CdT
В газах различают теплоемкость при постоянном объеме Сv и постоянном давлении Сp.
С |
v |
( |
dQ |
) |
U |
|
|
|
dU |
|
i |
kN |
|
i |
|
M |
R |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
dT |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
dT |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
С |
|
( |
dQ |
) |
|
|
|
|
dU PdV |
|
|
dU |
p( |
dV |
) |
|
|
C |
p( |
dV |
) |
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
P |
|
|
dT |
|
P |
|
|
|
|
|
|
dT |
|
|
|
|
|
|
dT |
|
|
|
|
dT |
P |
|
V |
dT |
P |
||||||||||||||||||||||
Для идеального газа V |
M |
|
RT |
( |
dV |
)P |
M |
|
R |
|
=> |
|
|
||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
P |
|
|
|
|
|
dT |
|
|
|
P |
|
|
|
|||||||
С |
P |
C |
V |
|
M |
R |
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
CP |
1 |
2 |
|
|
|
|
|
|
|
|
|
|
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
CV |
|
i |
|
|
|
|
|
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
2. Равновесные процессы в идеальных газах.
а) Изотермический T=const
PV const
б) Изохорический V=const
|
P |
const |
|
PV |
M |
RT |
|
|
|
|
|
|
|||
|
T |
|
|
|
|||
в) Изобарный P=const |
|
|
|
||||
|
|
|
|||||
|
V |
const |
|
|
|
|
|
|
|
|
|
||||
|
T |
|
|
|
|
||
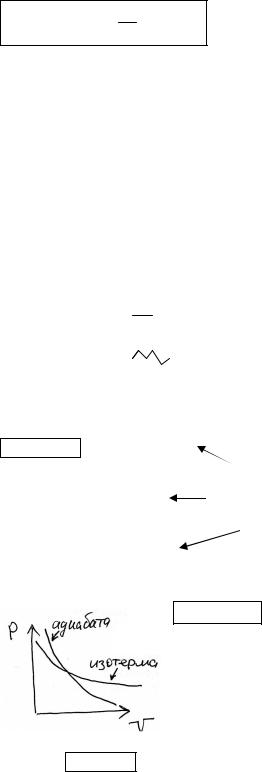
г) Адиабатический ∆Q=0 |
|
|
|
||||
PV const
3. Энтропия. Второе начало термодинамики.
Энтропия S kln , где - статистический вес состояния системы – число микросостояний системы, отвечающее данному макросостоянию.
Энтропия – аддитивная функция состояния системы. S=S1+S2+S3..<=( =П i)
Замкнутая система всегда стремится к равновесному состоянию. Равновесное состояние является наиболее вероятным, т. е. реализуется максимальным числом микросостояний => Второе начало термодинамики: в замкнутой системе энтропия не убывает.

dS 0
Равенство, если все процессы обратимые, больше, если необратимые.
Примеры необратимых процессов: диффузия, теплопроводимость.
4.Термодинамическое понятие энтропии. Исторические формулировки II начала термодинамики.
dS ( Q)обрат Формула применима только для обратимых
T
процессов.
Q - тепло, сообщаемое системе. Т – температура системы.
В случае идеального газа:
dS |
Q |
|
dU pdV |
C |
|
|
dT |
|
|
M |
R |
dV |
||||||||
|
|
|
|
|
|
|
|
|||||||||||||
|
T |
|
T |
|
|
|
|
V T |
|
|
|
|
|
V |
||||||
2 |
Q |
|
|
T |
|
|
M |
|
|
|
V |
2 |
|
|
|
|
|
|||
S |
|
|
CV ln |
2 |
|
|
|
Rln |
|
|
|
|
|
|
|
|||||
T |
T |
|
|
|
V |
|
|
|||||||||||||
1 |
|
|
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
Исторические формулировки II начала термодинамики:
1.Невозможен процесс, единственным результатом которого является передача тепла от холодного тела к горячему.
2.Невозможен процесс, единственным результатом которого является совершение работы за счет охлаждения тела.
Доказывается, что термодинамическое определение энтропии и исторические формулировки II начала термодинамики эквивалентны статистическим.
Вопросы:
1.Первое начало термодинамики.
2.Что такое теплоемкость тела, удельная теплоемкость тела, молярная теплоемкость?
3.Что такое CP и СV в газах, их связь для идеального газа.
4.Что такое энтропия, статистическая и термодинамическая формулировки.
5.Второе начало термодинамики, статистическая и исторические формулировки.
