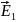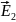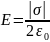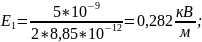3 семестр / IDZ1_Bochkarev
.docxВариант № 5
На расстоянии 20 см находятся два точечных заряда –40 нКл и +60 нКл. Определить силу, действующую на заряд – 10 нКл, удаленный от обоих зарядов на расстояние 25 см.


Дано: q1= -40 нКл; q2= +60 нКл; d= 20 см; r1=r2= 25 см; q= -10 нКл. |
СИ -40*10-9 Кл +60*10-9 Кл 0,2 м 0,25 м -10-9Кл |
B
q
r2
r1
C
A
d
q1
q2
Так
как q1 и q
отрицательные, а q2
положительный, то q и q1
будут отталкиваться с силой
,
а q и q2
будут притягиваться с силой
.
Используя принцип суперпозиции
получаем результирующую силу
=
Для нахождения модуля вектора необходимо воспользоваться теоремой косинусов
Угол
между векторами
F1 и F2
можно найти по теореме косинусов
из треугольника АВС, а именно угол при
вершине В вместе с углом
образует развернутый угол ,
тогда угол при вершине В будет
Для нахождения сил F1 и F2 воспользуемся законом Кулона, а именно:
Где
Подставляем, вычисляем:
Ответ: ~ 6,33*10-6 Н
|
Найти: F=? |
Тонкий длинный стержень заряжен равномерно. На расстоянии 10 см от стержня вблизи его середины находится заряд величиной 20нКл. Стержень действует на заряд с силой 18 мН. Определить линейную плотность заряда на стержне.
Дано: Q= 20 нКл; F= 18 мН; а= 10 см; |
СИ 20*10-9 Кл 18*10-3 Н 0,1 м
|
Q
d
а
r
rd
dl
Для
нахождения линейной плотности будем
использовать закон Кулона. Однако, он
применим для точечных зарядов, поэтому
разобьем наш стержень на бесконечно
малые элементы dl, заряд
которых будет
Далее
по соотношениям катетов и углов из
маленького треугольника выделяем
Вектор
интегрировать нельзя, надо разложить
на составляющие, с помощью которых
можно найти модуль (в условиях).
Разложение
на х и у
Проекция
на х нам не интересна, так как интеграл
синуса будет косинус, который в заданных
интервалах будет обращаться в 0, а вот
проекция на у равна
Выделяем искомую линейную плотность
Ответ:
5 |
Найти: =? |
Заряженные шарики, находящиеся на расстоянии 1 м друг от друга, притягиваются с силой 1 Н. Общий заряд шариков равен 20 мкКл. Как распределен этот заряд между шариками?
Дано: Q= 20 мкКл; F= 1 Н; l= 1 м; |
СИ 20*10-6 Кл 1 Н 1 м
|
Решение: По определению сила Кулона равна:
Из
условия задачи допустим, что q2
отрицательно заряженная частица,
тогда
Перенесем все в левую часть и решим уравнение:
Тогда
Ответ:
|
Найти: q1=?; q2=? |
Фарфоровый сплошной шар диаметром 5 см несет заряд, равномерно распределенный с объемной плотностью 1мкКл/м3. Определить напряженность и смещение электрического поля на расстоянии 3 см от центра шара.
Дано: D= 5 см; = 1 мкКл/м3; R= 3см ; |
СИ 5*10-2 м 10-6 Кл/м3 3*10-2 м
|
Решение: Воспользуемся
теоремой Гаусса для поля
Искомая точка лежит вне сферы (R>r), тогда
Ответ:
|
Найти:
=? |
Электрическое поле создано двумя бесконечными пластинами, несущими равномерно распределенный по площади заряд с поверхностными плотностями 5 нКл/м2 и –2 нКл/м2. Определить напряженность поля между пластинами.
Дано: 1= 5 нКл/м2; 2= -2 нкКл/м2; |
СИ 5*10-9 Кл/м2 -2*10-9 Кл/м2 |
+ -
Напряженность
поля равномерно заряженной бесконечной
пластины
Е1>E2, тогда итоговая E между пластинами будет
Ответ:
|
Найти: =?; |






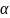


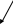


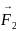



 .
.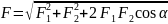
 ,
тогда
,
тогда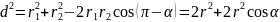 ,
отсюда
,
отсюда


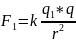
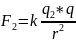

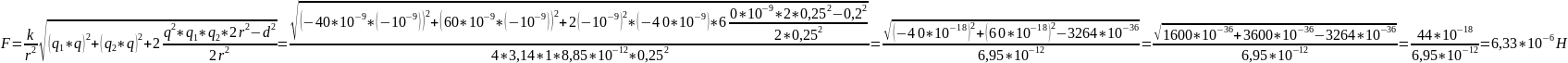
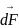

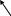


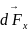
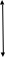






 ,
тогда известная нам сила, с которой
стержень действует на заряд будет
,
тогда известная нам сила, с которой
стержень действует на заряд будет
 ,
из большого
,
из большого
 ,
подставляем, получаем:
,
подставляем, получаем: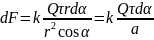

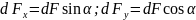


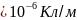

 ,
выразим один заряд через другой
,
выразим один заряд через другой
 и подставим в 1 выражение:
и подставим в 1 выражение: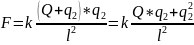
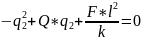

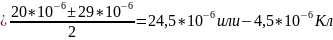


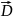 и связью векторов
и связью векторов
 :
:

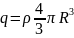 для полного заряда;
для полного заряда;
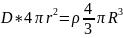

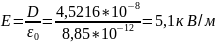
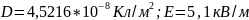
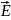 =?;
=?;