1.2 Схемы на основе сложности факторизации rsa-модуля
Схемы на основе сложности факторизации RSA-модуля относятся к криптографическим схемам, которые используют проблему факторизации больших целых чисел в криптографических вычислениях. RSA (Rivest-Shamir-Adleman) является одним из наиболее широко используемых алгоритмов для создания и проверки электронной подписи.
Схема RSA основана на математической задаче факторизации больших целых чисел. Ее сложность заключается в разложении большого составного числа на простые множители. Предполагается, что факторизация больших чисел является вычислительно сложной задачей, особенно когда числа имеют несколько сотен или тысяч цифр [4].
Схемы на основе сложности факторизации RSA-модуля используются для создания электронной подписи, аутентификации и шифрования данных. Подписывающая сторона использует закрытый ключ RSA для создания электронной подписи, которая включает в себя результат шифрования хэша (контрольной суммы) исходных данных. При проверке подписи получатель использует открытый ключ RSA для расшифровки подписи и сравнения полученного хэша с вычисленным хэшем от исходных данных.
Схемы на основе сложности факторизации RSA-модуля обеспечивают безопасность электронных данных, так как вычисление подписи требует знания закрытого ключа, который должен быть хранится в тайне. В то же время, проверка подписи может быть выполнена с использованием открытого ключа, который может быть распространен широко [5].
2 Математическое описание и разработка блок-схем алгоритмов эцп
2.1 Теоретические сведения о модуле
В криптографии одним из основных модулей, используемых в алгоритмах, является модуль операций над целыми числами. Он определяет операции, такие как сложение, вычитание, умножение и деление, которые выполняются в пределах заданного модуля. В контексте RSA-криптографии, модуль обычно представляет собой большое простое число, которое служит основой для генерации ключей и выполнения арифметических операций.
Операции над числами в модуле выполняются с использованием арифметики по модулю. Это означает, что результат каждой операции будет иметь остаток от деления на модуль. Например, в операции сложения, сумма двух чисел будет иметь остаток от деления на модуль. Таким образом, модуль определяет диапазон значений, в котором выполняются операции.
Использование модуля в криптографии обеспечивает безопасность и надежность операций. Большие модули обеспечивают сложность факторизации и обратного расчета, что делает их основой для алгоритмов шифрования и генерации электронно-цифровых подписей.
Важно выбирать модули, которые обладают определенными свойствами, такими как простота и достаточная длина, чтобы обеспечить стойкость к взлому. Кроме того, модуль должен быть выбран таким образом, чтобы его факторизация была вычислительно сложной задачей, что обеспечит безопасность криптографических операций, выполняемых с его использованием [6].
В контексте RSA-модуля для нахождения обратного элемента от числа (экспонента) важно использовать модуль, который является произведением двух простых чисел (p и q). Обратный элемент вычисляется с использованием расширенного алгоритма Евклида.
Шаги для нахождения обратного элемента от числа в RSA-модуле:
Вычислите значение функции Эйлера от модуля RSA (φ(n)), где
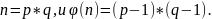
Убедитесь, что число, для которого вы хотите найти обратный элемент, взаимно просто с φ(n). Это означает, что число и φ(n) не имеют общих делителей, кроме 1.
С помощью расширенного алгоритма Евклида найдите коэффициенты x и y, удовлетворяющие уравнению
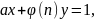где a - число, для которого вы хотите
найти обратный элемент, и φ(n) - функция
Эйлера.Обратный элемент от числа a по модулю
будет равен x. Если x отрицательное,
добавьте значение n, чтобы получить
положительный обратный элемент.
Важно отметить, что в RSA-шифровании обратный элемент используется для дешифрования или подписи сообщений, и его вычисление происходит только в процессе ключевой генерации. Обратный элемент не вычисляется при каждом шифровании или расшифровке сообщения [7].