АСВТ 4

МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ

РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное образовательное

учреждение высшего образования

«Юго-Западный государственный университет»

Лабораторная работа №4

По дисциплине «Аппаратные средства вычислительной техники»

Выполнил: Бунина А.В.

студент группы ИБ-01б

Проверил: Шевелев С.С.

доцент

Курск, 2022

Задание к лабораторной работе №4

1. Собрать схему счетчика с произвольным модулем в соответствии с заданным вариантом и провести её исследование. Построить временные диаграммы работы для выходных сигналов.

2. Произвести исследование комбинационных схем применение двоичных счетчиков в цифровых устройствах рис. 2.9 - 2.14.

3. Собрать дополнительные цепи сброса двоичных счетчиков, использую трехразрядные и четырехразрядные числа из таблицы 3 согласно заданного варианта, и провести их исследование.

4. Отчет по работе должен содержать:

- основные этапы синтеза синхронного счетчика с произвольным модулем и его схему;

- схему испытания и временные диаграммы работы счетчика с произвольным модулем;

- схемы дополнительных цепей сброса двоичных счетчиков рис. 2.9-2.14 согласно заданного варианта из таблицы 3.

№ Варианта	Трехразрядная дополнительная цепь сброса	Четырехразрядная дополнительная цепь сброса	Базис построения КСх цепи сброса
2.3	793	6593	ИЛИ-НЕ

Целью работы является освоение основных этапов изучение и функционирование схемных разновидностей двоичных счетчиков, анализа простейших цифровых схем с применением двоичных счетчиков, синтеза цифровых автоматов в указанных базисах, комбинационных схем типовых узлов вычислительной техники с использованием механизма имитационного моделирования программы Multisim.

Теоретические сведения

Двоичные счетчики. Счетчиком называют цифровое устройство (цифровой автомат), сигналы на выходе, которого, в определенном коде, отображают число импульсов, поступивших на счетный вход. Кроме того, в счётчиках выполняются такие микрооперации, как установка в исходное состояние, хранение и выдача слов. По мере поступления входных сигналов счетчик последовательно меняет свои состояния, образованные комбинациями состояний триггеров со счетным входом. Число разрешенных состояний счетчика называют модулем счета, коэффициентом пересчета или емкостью M (в общем случае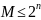 , где n - число триггеров или двоичных разрядов счетчика). Счетчики классифицируют по значению модуля, направлению счета и способу организации межразрядных связей.

По значению модуля счета различают: двоичные (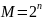 ), двоично-кодированные с произвольным модулем, с одинарным кодированием и др.

По направлению счета: суммирующие (прямого счета - Up-counter), вычитающие (обратного счета - Down-counter) и реверсивные (Up-Down-counter).

По способу организации межразрядных связей различают счетчики с последовательным, параллельным и комбинированным переносами.

Кроме того, все перечисленные типы счетчиков принято делить на два вида: синхронные и асинхронные. При этом в асинхронных счетчиках изменение его состояния, вызванное воздействием очередного импульса, характеризуется последовательным во времени изменением состояний триггеров (как правило, это счетчики с последовательным переносом). В синхронных счетчиках смена состояний характеризуется одновременным во времени изменением состояний его триггеров. В этом качестве синхронные счетчики образуют один из видов синхронных автоматов, потому к ним может быть применена и стандартная методика синтеза этого класса автоматов.

Определим некоторые закономерности двоичных счётчиков. Соответствие между числом входных импульсов и состояниями 3-разрядного двоичного счетчика (прямой и обратный счет) представлено в табл. 3.1. Рассматривая табл. 3.1 для прямого счета, можно отметить две закономерности:

1. Значение переменной Qi изменяется тогда, когда переменная в соседнем младшем разряде Qi-1 переходит из состояния «1» в состояние «0».

2. Значение выходной переменной Qi изменяется при поступлении очередного импульса счета в том случае, когда переменные во всех младших разрядах Qi-1, ..., Q1 находятся в состоянии «1».

Число входных импульсов	Суммирующий			Вычитающий
	Q3	Q2	Q1	Q3	Q2	Q1
0	0	0	0	1	1	1
1	0	0	1	1	1	0
2	0	1	0	1	0	1
3	0	1	1	1	0	0
4	1	0	0	0	1	1
5	1	0	1	0	1	0
6	1	1	0	0	0	1
7	1	1	1	0	0	0

Первая закономерность указывает на возможность реализации счетчика асинхронного типа, вторая позволяет построить синхронный счетчик. Для вычитающего счетчика аналогичные закономерности можно сформулировать так:

1. Значение выходной переменной Qi изменяется, когда переменная в соседнем младшем разряде Qi-1 переходит из состояния «0» в состояние «1».

2. Значение выходной переменной Qi изменяется при поступлении очередного импульса счета в том случае, когда все переменные в предыдущих младших разрядах Qi-1, ..., Q1 находятся в состоянии «0».

Выполнение работы

№ Варианта	Трехразрядная дополнительная цепь сброса	Четырехразрядная дополнительная цепь сброса	Базис построения КСх цепи сброса
2.3	793	6593	ИЛИ-НЕ

Для построения дополнительных цепей сброса в заданном базисе в первую очередь необходимо построить таблицу истинности для заданных значений:

Цифра	X4	X3	X2	X1
7	0	1	1	1
9	1	0	0	1
3	0	0	1	1

Для каждого значения запишем функцию и приведем ее к базису ИЛИ-НЕ:

; ;

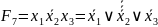Цифра	X4	X3	X2	X1
6	0	1	1	0
5	0	1	0	1
9	1	0	0	1
3	0	0	1	1

Для каждого значения запишем функцию и приведем ее к базису ИЛИ-НЕ:

; ; ;

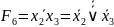Построим комбинационные схемы останова и обнуления двоичных счетчиков с применением генератора прямоугольных импульсов, двоичных счетчиков, дешифраторов и семисегментных индикаторов. (рис. 1, рис. 2)

Вывод: освоила и изучила основные этапы функционирования схемных разновидностей двоичных счетчиков, анализа простейших цифровых схем с применением двоичных счетчиков, синтеза цифровых автоматов в указанном базисе, комбинационных схем типовых узлов вычислительной техники с использованием механизма имитационного моделирования программы Multisim.

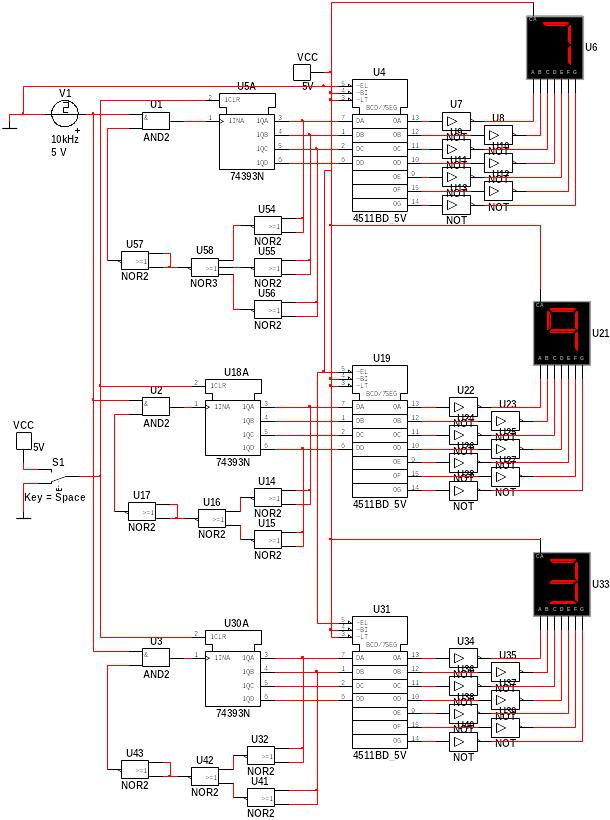
Рис. 3. Задание 1

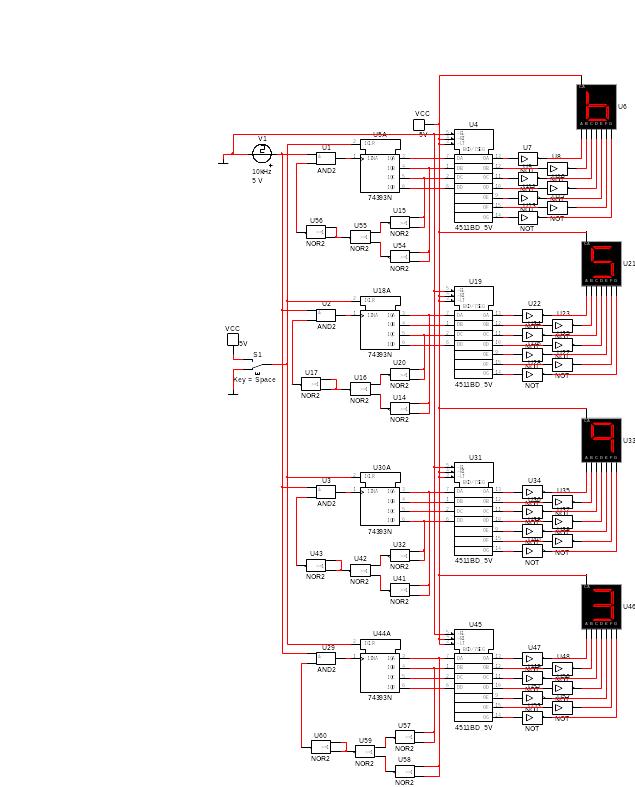
Рис. 4. Задание 2

Библиографический список

1. Каган Б.М. Электронные вычислительные машины и системы: Учебное пособие для вузов. – М.: Энергоатомиздат, 1991.- 592 с: ил.

2. Угрюмов Е. П. Проектирование элементов и узлов ЭВМ: и Учеб. пособие для вузов. – М.: Высшая Школа, 1987.-318 с.: ил.

3. Потемкин И. С. Функциональные узлы цифровой автоматики. – М.: Энергоатомиздат, 1988.-320 с.: ил. 40

4. Зельдин Е. А. Цифровые интегральные микросхемы в информационно-измерительной аппаратуре. – Л.: Энергоатомиздат, 1986.-280 с.: ил.

5. Пухальский Г.И., Новосельцева Т. Я. Проектирование дискретных устройств на интегральных микросхемах: Справочник. -М.: Радио и связь, 1990.-304 с.: ил.

6. Цифровые ЭВМ: Практикум / К.Г.Самофалов, В.И.Корнейчук, В.П.Тарасенко; Под общ. ред. К.Г.Самофалова. - К.: Выща шк.,1990.-225с.:Ил

7. Скляров В. А. Синтез автоматов на матричных БИС / Под. Ред. С. И. Баранова. – Минск: Наука и техника, 1984.-288 с.: ил. 8. . Угрюмов Е. П. Цифровая схемотехника.- СПб.: БХВ – Санкт-Петербург, 2000. – 528 с.: ил