40. Поведение функции вблизи устранимой особой точки и вблизи точки типа полюс. Примеры.

1. Если изолированная особая точка является устранимой, то существует конечный предел .

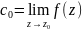Пример: в функции особой точкой является z = 0.

Отсюда , таким образом точка z является устранимой.

2. Если изолированная особая точка является полюсом, то предел функции в этой точке равен бесконечности

Пример: функция имеет в нуле полюс второго порядка, так как (функция совпадает с рядом Лорана в нуле).

41. Поведение функции вблизи существенно особой точки. Пример. Теорема Сохоцкого-Вейерштрасса.

В окрестности существенно особой точки функция не определена.

Пример: – главная часть содержит бесконечное число членов, поэтому z = 0 является существенно особой.

Теорема Сохоцкого - Вейерштрасса

Однозначная аналитическая функция в окрестности существенно особой точки может принимать значения, близкие к любым заранее заданным комплексным числам.

42. Понятие вычета в изолированной особой точке. Вычет в устранимой особой точке. Вычисление вычета в существенно особой точке. Примеры.

Вычетом в изолированной особой точке называется число

, где С - окружность, охватывающая точку и лежащая в её проколотой окрестности, где функция аналитична.

Вычет в устранимой особой точке равен нулю , так как в данной точке главная часть ряда Лорана отсутствует.

Чтобы найти вычет в существенно особой точке, надо записать разложение функции в ряд Лорана и взять коэффициент при , либо посчитать вычет по определению.

43. Вычисление вычета в полюсе первого порядка.

Разложим функцию f(z) в ряд Лорана в полюсе первого порядка:

Умножим обе части на и возьмём предел

44. Вычисление вычета в полюсе порядка m>1.

45. Теоремы (основная и вторая) теории вычетов.

46. Ортогональные и ортонормированные системы. Ортогональность тригонометрической системы.

Последовательность попарно различных элементов евклидова пространства называется ортогональной системой, если любые два элемента попарно ортогональны, то есть их скалярное произведение равно нулю

Путём деления на норму каждого элемента ортогональной системы можно получить ортонормированную систему:

Тригонометрическая система функций , является ортогональной на отрезке длины , то есть интеграл по этому отрезку от любых двух различных функций этой системы равен нулю.

47. Ряд Фурье в действительной форме. Формулы для вычисления коэффициентов.

Ряд называется рядом Фурье в действительной форме.

48. Ряд Фурье в комплексной форме

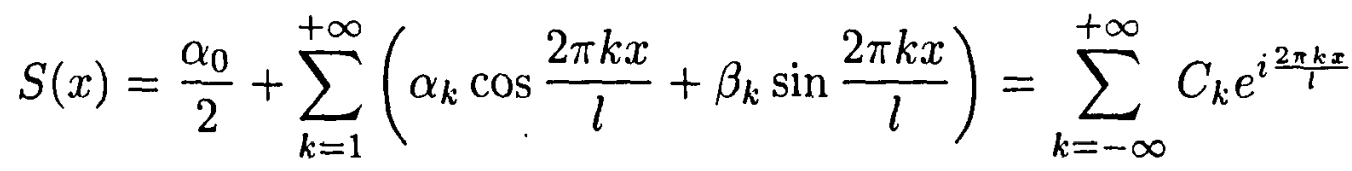
49. Кусочно-непрерывные и кусочно-гладкие функции. Теоремы о сходимости и равномерной сходимости ряда Фурье для кусочно-гладких функций

50. Понятие оригинала, показатель роста функции.

51. Преобразования Лапласа, теорема о сходимости интеграла

52. Изображение и теорема об аналитичности изображения

53. Свойства преобразования Лапласа

54. Теоремы запаздывания и смещения

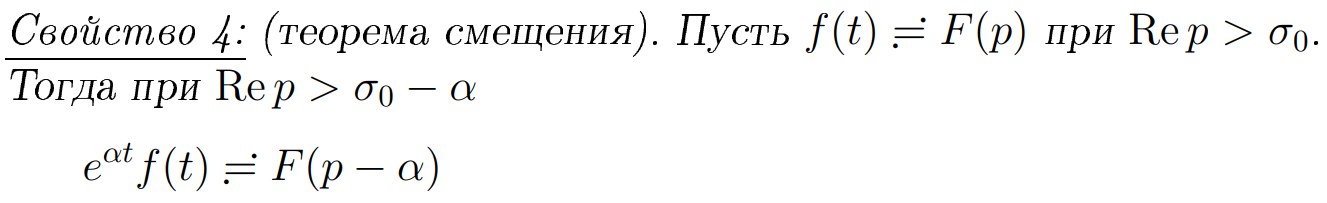
55. Теоремы о дифференцировании

56. Теоремы об интегрировании

Решение задач из типового билета:

1. Найти область сходимости и сумму ряда

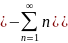
Признак Даламбера:

Ответ: область сходимости - открытый круг радиуса 1 с центром в точке (0 ; 1), .

2. Найти вычет функции относительно каждого из её полюсов

z = 1 - полюс n-го порядка;

.
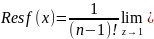