Ответы на философские вопросы математического анализа или ещё один способ заварить кашу в своей голове

1. Комплексное число, действия с комплексными числами. Модуль и аргумент комплексного числа

Комплексное число – выражение вида x+iy , где x и у – действительные числа, а i – мнимая единица, удовлетворяющая соотношению i*i = -1. Числа x и y называют действительной и мнимой частью комплексного числа x+iy соответственно.

Формальные действия с комплексными числами:

1) Сложение :

2) Вычитание:

3) Умножение:

4) Комплексное сопряжение:

Свойство:

а)

б)

в)

г)

5) Деление:

6) Возведение в натурал. степень: n раз умножаем)

Комплексная плоскость - это декартова система координат, точки оси абсцисс которой соответствуют действительным числам, а чисто мнимым - точки оси ординат.

Тригоном. форма записи комплекс. числа:

Arg - значение аргумента числа z (имеет бесконечно много значений)

arg - главное значение аргумента, соответствующее тому значению Arg , которое лежит между pi и -pi (исключая -pi и включая pi)

2. Понятие области. Стереографическая проекция и бесконечно удаленная точка

Область G комплексной плоскости - множество точек, в котором каждая точка z имеет окрестность, принадлежащая множеству (открытость множества), и каждые две точки можно соединить ломаной, принадлежащей множеству (связность множества).

Пример: (открытый круг радиуса 5).

Стереографическая проекция - отображение точек сферы на плоскость.

То есть каждому прообразу из сферы ставится в соответствие единственный образ на плоскости, кроме северного полюса N.

Бесконечно удаленная точка ( - образ точки N [северного полюса], лежащий бесконечно далеко от образа южного полюса S [то есть от самого полюса по сути]

Таким образом, при добавлении бесконечно удалённой точки в качестве границы получаем расширенную комплексную плоскость, называемую сферой Римана.

3. Последовательности комплексных чисел. Ограниченная и бесконечно большая последовательности. Предел последовательности комплексных чисел.

Последовательностью комплексных чисел называется упорядоченное счётное множество комплексных чисел .

Последовательность является ограниченной, если

Последовательность называется бесконечно большой, если

Комплексное число z называется пределом последовательности , если

4. Функция комплексного переменного. Однозначные и многозначные функции. Предел функции комплексного переменного. Непрерывность функции комплексного переменного.

Функцией комплексного переменного называют закон (правило), по которому комплексное число z из множество задания D ставится в соответствие числу из множества изменения E.

5. Определение показательной, логарифмической, степенной, тригонометрических, гиперболических функций комплексного переменного.

6. Определение обратных тригонометрических функций комплексного переменного

7. Производная функции комплексного переменного. Условия Коши-Римана.

Однозначная функция f(z) является дифференцируемой в точке z, если существует конечный предел отношения

Условия Коши-Римана:

- доказываются тем фактом, что предел не зависит от способа приближения к точке z.

Производную функции можно представить различными способами:

8. Понятие аналитичности функции. Необходимое и достаточное условие аналитичности функции.

Однозначная функция является аналитической в области G, если она определена и дифференцируема во всех точках области G и её производная непрерывна в ней.

9. Свойства аналитических функций (формулировки)

Следующие композиции аналитических функций f, g являются также аналитическими:

1. 

2. 

3. 

Если функция f(z) аналитична и определена на подмножестве множества изменения функции g(z), то следующая функция является аналитической

В некоторой окрестности W точки определена аналитическая обратная функция , причём

Такие функции называют гармоническими.

10. Аналитичность показательной, степенной, тригонометрических и гиперболических функций.

Тригонометрические и гиперболические функции являются аналитическими, так как являются композициями аналитической функции .

11. Интеграл по кривой в комплексной плоскости (определение и связь с интегралами 2-го рода)

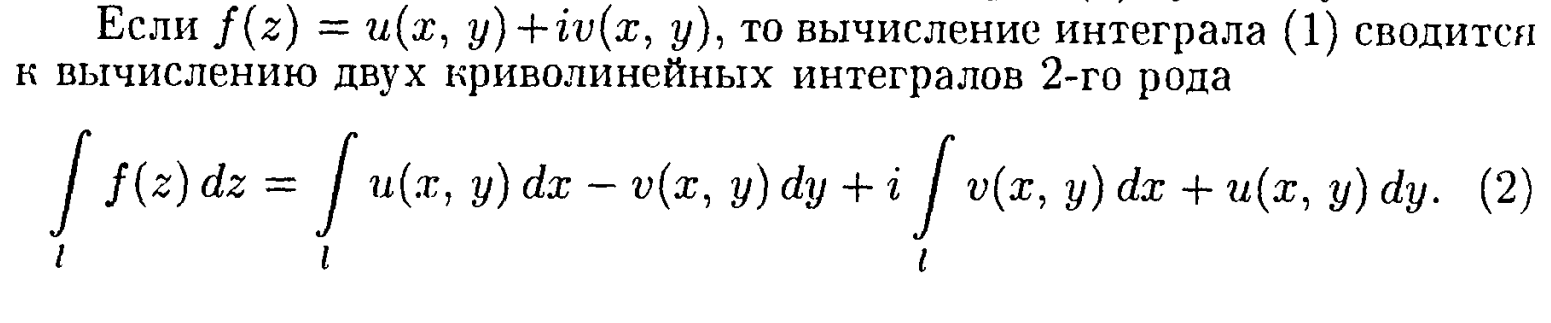
12. Свойства интеграла по кривой в комплексной плоскости.

13. Теорема Коши для односвязной области

[В квадратных скобках содержатся пояснения, их не надо писать в ответе на вопрос, но необходимо понимать, о чём идёт речь, чтобы можно было ответить на дополнительные устные вопросы, если они будут.]

[Односвязная область - это множество точек, в которой любую замкнутую кривую можно стянуть к точке]

[Область G является замкнутой, если она имеет границу ]

[В интегрировании важно, чтобы кривые, в том числе и граница области, были гладкими или кусочно гладкими (объединение гладких кривых), ведь только тогда может существовать касательная к этим кривым, что является геометрическим смыслом производной]

[Пусть в области G функция f(z) является аналитической, то есть она имеет непрерывные первые частные производные в этой области, которые связаны условиями Коши-Римана. Вообще, непрерывность должна быть везде, то есть функция должна иметь в каждой точке конечное значение, иначе мы просто не сможем продифференцировать и проинтегрировать что-либо. Если функция f(z) является ещё непрерывной на границе области , то функция является аналитической в замкнутой области .]

[Из второго семестра здесь пригодится формула Грина:

]

Теорема Коши для односвязной области:

Пусть в односвязной области G с кусочно гладкой границей функция f(z) является аналитической, тогда интеграл от функции по замкнутой границе области равен 0:

Доказательство:

Так как функция f(z) аналитична в G, то существует непрерывная производная в G. Пусть такая производная существует и на границе , тогда первые частные производные тоже непрерывны на границе. И так как функция по условию аналитична в замкнутой области, то она непрерывна на границе, а значит функции u(x,y) и v(x,y) тоже непрерывны [напомню, что f(z) = u+i*v]. Поэтому мы можем воспользоваться связью интеграла по кривой в комплексной плоскости с криволинейными интегралами второго рода:

= [было использовано условие Коши-Римана]

Отсюда следует вторая формулировка теоремы Коши для односвязной области: Если f(z) - аналитическая в односвязной области G, то для любого замкнутого кусочно-гладкого контура C внутри области верно

14. Теорема Коши для многосвязной области Пусть функция f(z) аналитична в многосвязной замкнутой области , ограниченной снаружи контуром , а изнутри контурами … .

Тогда

Доказательство:

Представим себе заданную область:

15. Первообразная аналитической функции комплексного переменного

По теореме Коши для замкнутого контура при непрерывной функции f(z) в области G для контура , целиком лежащего в G, верно

В таком случае существует аналитическая функция - первообразная функция комплексного аргумента:

, где интеграл берётся по кусочно-гладкой кривой, соединяющей точки , причём его значение не зависит от этой кривой и .

16. Интегральная формула Коши

Пусть - область, в которой функция f(z) является аналитической и

Тогда существует интеграл Коши

Пример

Запишем интеграл в виде

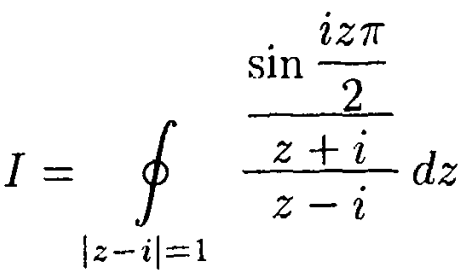
и, используя формулу Коши, находим

17. Формула Коши для производных аналитической функции

При этом все производные являются аналитическими.

Пример

Вычислить интеграл

Из-за того, что в знаменателе z фигурирует в кубе, мы не можем использовать интегральную формулу Коши. Воспользуемся формулой для производных:

18. Сходимость числового ряда. Сумма сходящихся рядов. Критерий Коши сходимости ряда

Бесконечная сумма членов последовательности называется рядом

Конечные суммы называются частичными суммами ряда.

Числовой ряд называется сходящимся, если сходится последовательность его частичных сумм , где S - сумма ряда.

Критерий коши сходимости ряда:

Для сходимости ряда необходимо и достаточно, чтобы

19. Критерий Коши сходимости ряда (формулировка). Необходимое условие сходимости числового ряда.

[Видимо, здесь повтор критерия Коши]

Критерий коши сходимости ряда:

Для сходимости ряда необходимо и достаточно, чтобы

Необходимое условие сходимости ряда

Если ряд сходится, то

Доказательство:

В критерии Коши можно взять m=1, тогда получим , что эквивалентно

20. Расходимость гармонического ряда

Рассмотрим гармонический ряд . Возьмём любое n и m = n и составим остаток ряда

Критерий Коши не выполняется, значит, гармонический ряд расходится.

21. Абсолютная и условная сходимость. Связь между сходимостью и абсолютной сходимостью. Пример.

Ряд называется абсолютно сходящимся, если сходится ряд из его модулей .

Если ряд из модулей расходится, а сам ряд сходится, то он сходится условно.

Теорема:

Если ряд сходится абсолютно, то он сходится в обычном смысле

Доказательство: Если ряд из модулей сходится, то по критерию Коши

Для сходимости ряда необходимо и достаточно, чтобы .

Известно, что , что доказывает теорему.

Примером условно сходящегося ряда является знакочередующийся гармонический ряд

22. Первый признак сравнения рядов (формулировка). Пример.

Примеры:

23. Предельный признак сравнения рядов (формулировка). Пример.

Примеры:

24. Признак Даламбера (формулировка). Пример.

Примеры:

25. Радикальный признак Коши (формулировка). Пример

Примеры:

26. Интегральный признак Коши (формулировка). Пример.

Примеры:

27. Признак Лейбница (формулировка). Пример.

Примеры:

28. Функциональные ряды. Область сходимости. Равномерная сходимость (на примере геометрической прогрессии).

Бесконечная сумма членов последовательности функций комплексной переменной называется функциональным рядом

Область сходимости функционального ряда - комплексная область G, в котором при любом соответствующий числовой ряд сходится к комплексному числу f(z), называемый суммой ряда.

Ряд называется равномерно сходящимся к f(z), если

[То есть график частичной суммы полностью лежит в эпсилон-окрестности функции f(z), к которой сходится ряд.]

Рассмотрим геометрическую прогрессию .

Ряд сходится при к функции [формула суммы геометрической прогрессии]. Чтобы определить равномерную сходимость, выделим остаток ряда .

При

При при n нечётных или при n чётных

При остальных . [Помните, что |x|<1, поэтому ноль, а не бесконечность].

Таким образом, геометрическая прогрессия сходится неравномерно, так как при и график остатка ряда выходит за границу эпсилон окрестности функции (f(x) = 0).