Лабораторная работа №2 (2 часть).

Отладка вызовов функций и рекурсии.

Очень часто в программировании необходимо выполнять одни и те же действия. Например, мы хотим выводить пользователю сообщения об ошибке в разных местах программы, если он ввел неверное значение. Без функций это выглядело бы так:

#include <iostream>

#include <string>

using namespace std;

int main()

{

string valid_pass = "qwerty123";

string user_pass;

cout << "Введите пароль: ";

getline(cin, user_pass);

if (user_pass == valid_pass)

{

cout << "Доступ разрешен." << endl;

}

else

{

cout << "Неверный пароль!" << endl;

}

return 0;

}

Аналогичный пример с функцией:

#include <iostream>

#include <string>

using namespace std;

void check_pass (string password)

{

string valid_pass = "qwerty123";

if (password == valid_pass) {

cout << "Доступ разрешен." << endl;

} else {

cout << "Неверный пароль!" << endl;

}

}

int main()

{

string user_pass;

cout << "Введите пароль: ";

getline (cin, user_pass);

check_pass (user_pass);

return 0;

}

После компиляции не будет никакой разницы для процессора, как для первого кода, так и для второго. Но ведь такую проверку пароля мы можем делать в нашей программе довольно много раз. И тогда получается многократное повторение и код становится нечитаемым. Функции — один из самых важных компонентов языка C++.

Свойства функции:

• Любая функция имеет тип, так же, как и любая переменная.

• Функция может возвращать значение, тип которого в большинстве случаев аналогично типу самой функции.

• Если функция не возвращает никакого значения, то она должна иметь тип void (такие функции иногда называют процедурами)

• При объявлении функции, после ее типа должно находиться имя функции и две круглые скобки — открывающая и закрывающая, внутри которых могут находиться один или несколько аргументов функции, которых также может не быть вообще.

• после списка аргументов функции ставится открывающая фигурная скобка, после которой находится само тело функции.

• В конце тела функции обязательно ставится закрывающая фигурная скобка.

Пример №1 построения функции:

Всем известная тривиальная программа, Hello, world, только реализованная с использованием функций.

#include <iostream>

using namespace std;

void function_name ()

{

std::cout << "Hello, world" << std::endl;

}

int main()

{

function_name(); // Вызов функции

return 0;

}

Если мы хотим вывести «Hello, world» где-то еще, нам просто нужно вызвать соответствующую функцию. В данном случае это делается так: function_name();. Вызов функции имеет вид имени функции с последующими круглыми скобками. Эти скобки могут быть пустыми, если функция не имеет аргументов. Если же аргументы в самой функции есть, их необходимо указать в круглых скобках.

Также существует такое понятие, как параметры функции по умолчанию. Такие параметры можно не указывать при вызове функции, т.к. они примут значение по умолчанию, указанно после знака присваивания после данного параметра и списке всех параметров функции.

В предыдущих примерах мы использовали функции типа void, которые не возвращают никакого значения. Оператор return используется для возвращения вычисляемого функцией значения.

Рассмотрим пример функции, возвращающей значение на примере проверки пароля.

#include <iostream>

#include <string>

using namespace std;

string check_pass (string password)

{

string valid_pass = "qwerty123";

string error_message;

if (password == valid_pass) {

error_message = "Доступ разрешен.";

} else {

error_message = "Неверный пароль!";

}

return error_message;

}

int main()

{

string user_pass;

cout << "Введите пароль: ";

getline (cin, user_pass);

string error_msg = check_pass (user_pass);

cout << error_msg << endl;

return 0; }

В данном случае функция check_pass имеет тип string, следовательно, она будет возвращать только значение типа string, иными словами говоря, строку. Давайте рассмотрим алгоритм работы этой программы.

Самой первой выполняется функция main(), которая должна присутствовать в каждой программе. Теперь мы объявляем переменную user_pass типа string, затем выводим пользователю сообщение «Введите пароль», который после ввода попадает в строку user_pass. Дальше начинает работать наша собственная функция check_pass().

В качестве аргумента этой функции передается строка, введенная пользователем.

Аргумент функции — это, говоря простым языком, переменная или константа вызывающей функции, которые будет использовать вызываемая функция.

При объявлении функций создается формальный параметр, имя которого может отличаться от параметра, передаваемого при вызове этой функции. Но типы формальных параметров и передаваемых функции аргументов в большинстве случаев должны быть аналогичны.

После того, как произошел вызов функции check_pass(), начинает работать данная функция. Если функцию нигде не вызвать, то этот код будет проигнорирован программой. Итак, мы передали в качестве аргумента строку, которую ввел пользователь.

Теперь эта строка в полном распоряжении функции. Обращаем ваше внимание на то, что переменные и константы, объявленные в разных функциях независимы друг от друга, они даже могут иметь одинаковые имена.

Теперь мы проверяем, правильный ли пароль ввел пользователь. Если пользователь ввел правильный пароль, присваиваем переменной error_message соответствующее значение. Если нет, то сообщение об ошибке.

После этой проверки мы возвращаем переменную error_message. На этом работа нашей функции закончена. А теперь, в функции main() то значение, которое возвратила наша функция. Мы присваиваем переменной error_msg и выводим это значение (строку) на экран терминала.

Также, можно организовать повторный ввод пароля с помощью рекурсии (когда функция вызывает сама себя).

Пример №2 построения функции:

#include <iostream>

#include <string>

using namespace std;

bool password_is_valid (string password)

{

string valid_pass = "qwerty123";

if (valid_pass == password)

return true;

else

return false;

}

void get_pass ()

{

string user_pass;

cout << "Введите пароль: ";

getline(cin, user_pass);

if (!password_is_valid(user_pass)) {

cout << "Неверный пароль!" << endl;

get_pass (); // Здесь делаем рекурсию

} else {

cout << "Доступ разрешен." << endl;

}

}

int main()

{

get_pass ();

return 0;

}

Вывод: Функции очень сильно облегчают работу программисту и повышают читаемость и понятность кода, в том числе и для самого разработчика.

Рекурсия в С++

Рекурсия достаточно распространённое явление, которое встречается не только в областях науки, но и в повседневной жизни. Например, эффект Дросте, треугольник Серпинского и т. д. Самый простой вариант увидеть рекурсию – это навести включенную Web-камеру на экран монитора компьютера. Таким образом, камера будет записывать изображение экрана компьютера, и выводить его же на этот экран, получится что-то вроде замкнутого цикла. В итоге мы будем наблюдать нечто похожее на тоннель.

В программировании рекурсия тесно связана с функциями, точнее именно благодаря функциям в программировании существует такое понятие как рекурсия или рекурсивная функция. Проще говоря, рекурсия – это функция, которая вызывает саму себя, непосредственно (в своём теле) или косвенно (через другую функцию). Типичными рекурсивными задачами являются задачи: нахождения n!, числа Фибоначчи. Такие задачи мы уже решали, но с использованием циклов, то есть итеративно. Из этого можно сделать вывод: всё то, что решается итеративно можно решить рекурсивно, то есть с использованием рекурсивной функции. Всё решение сводится к решению основного или, как ещё его называют, базового случая. Существует такое понятие как шаг рекурсии или рекурсивный вызов. В случае, когда рекурсивная функция вызывается для решения сложной задачи (не базового случая) выполняется некоторое количество рекурсивных вызовов или шагов, с целью сведения задачи к более простой. И так до тех пор пока не получим базовое решение.

Разработаем программу, в которой объявлена рекурсивная функция, вычисляющая n! .

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30

// factorial.cpp: определяет точку входа для консольного приложения. #include "stdafx.h" #include <iostream> using namespace std;   unsigned long int factorial(unsigned long int); // прототип рекурсивной функции int i = 1; // инициализация глобальной переменной для подсчёта кол-ва рекурсивных вызовов unsigned long int result; // глобальная переменная для хранения возвращаемого результата рекурсивной функцией   int main(int argc, char* argv[]) {            int n; // локальная переменная для передачи введенного числа с клавиатуры        cout << "Enter n!: ";        cin >> n;        cout << n << "!" << "=" << factorial(n) << endl; // вызов рекурсивной функции        system("pause");        return 0; }   unsigned long int factorial(unsigned long int f) // рекурсивная функция для нахождения n! {        if (f == 1 || f == 0) // базовое или частное решение              return 1; // все мы знаем, что 1!=1 и 0!=1        cout << "Step\t" << i << endl;        i++; // операция инкремента шага рекурсивных вызовов        cout << "Result= " << result << endl;        result = f * factorial(f - 1); // функция вызывает саму себя, причём её аргумент уже на 1 меньше        return result; }

В строках 7, 9, 21 объявлен тип данных unsigned long int, так как значение факториала возрастает очень быстро, например уже 10! = 3 628 800. Если не хватит размера типа данных, то в результате мы получим неправильное значение. В коде объявлено больше операторов, чем нужно, для нахождения n!. Это сделано для того, чтобы, отработав, программа показала, что происходит на каждом шаге рекурсивных вызовов.

Обратите внимание на выделенные строки кода, строки 23, 24, 28 - это рекурсивное решение n!. Строки 23, 24 являются базовым решением рекурсивной функции, то есть, как только значение в переменной f  будет равно 1 или 0 (так как мы знаем, что 1! = 1 и 0! = 1), прекратятся рекурсивные вызовы, и начнут возвращаться значения, для каждого рекурсивного вызова. Когда вернётся значение для первого рекурсивного вызова, программа вернёт значение вычисляемого факториала. В строке 28 функция factorial() вызывает саму себя, но уже её аргумент на единицу меньше. Аргумент каждый раз уменьшается, чтобы достичь частного решения. Результат работы программы (см. Рисунок 1).

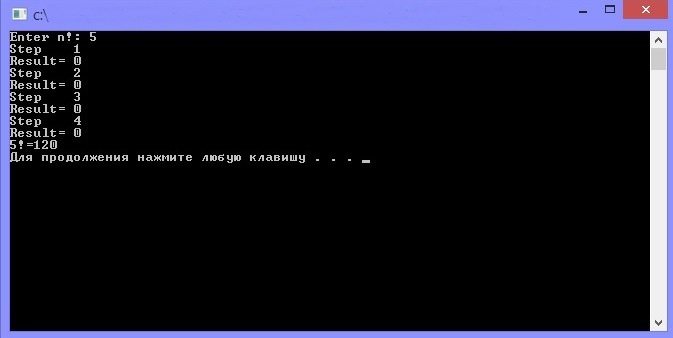
Рисунок 1. Результат работы программы.

По результату работы программы хорошо виден каждый шаг и результат на каждом шаге равен нулю, кроме последнего рекурсивного обращения. Необходимо было вычислить пять факториал. Программа сделала четыре рекурсивных обращения, на пятом обращении был найден базовый случай. И как только  программа получила решение базового случая, она порешала предыдущие шаги и вывела общий результат. 

На рисунке 1 видно всего четыре шага потому, что на пятом шаге было найдено частное решение, что  в итоге вернуло конечное решение, т. е. 120.

На рисунке 2 показана схема рекурсивного вычисления 5!. В схеме хорошо видно, что первый результат возвращается, когда достигнуто частное решение, но никак не сразу, после каждого рекурсивного вызова.

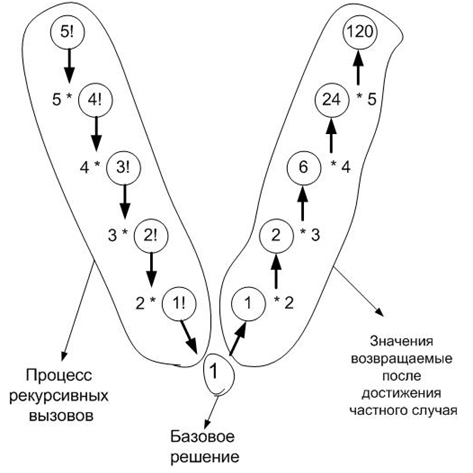
Рисунок 2. Схема рекурсивного вычисления 5!.

Итак, чтобы найти 5! нужно знать 4! и умножить его на 5; 4! = 4 * 3! и так далее. Согласно схеме, изображённой на рисунке 2, вычисление сведётся к нахождению частного случая, то есть 1!, после чего по очереди будут возвращаться значения каждому рекурсивному вызову. Последний рекурсивный вызов вернёт значение 5!.

Переделаем программу нахождения факториала так, чтобы получить таблицу факториалов. Для этого объявим цикл for, в котором будем вызывать рекурсивную функцию.

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33

// factorial.cpp: определяет точку входа для консольного приложения.   #include "stdafx.h" #include <iostream> using namespace std;   unsigned long int factorial(unsigned long int);// прототип рекурсивной функции int i = 1; // инициализация глобальной переменной для подсчёта кол-ва рекурсивных вызовов unsigned long int result; // глобальная переменная для хранения возвращаемого результата рекурсивной функцией   int main(int argc, char* argv[]) {            int n; // локальная переменная для передачи введенного числа с клавиатуры        cout << "Enter n!: ";        cin >> n;        for (int k = 1; k <= n; k++ )        {         cout << k << "!" << "=" << factorial(k) << endl; // вызов рекурсивной функции        }        system("pause");        return 0; }   unsigned long int factorial(unsigned long int f) // рекурсивная функция для нахождения n! {        if (f == 1 || f == 0) // базовое или частное решение              return 1; // все мы знаем, что 1!=1 и 0!=1        //cout << "Step\t"<< i <<endl;        i++;        //cout <<"Result= "<< result << endl;        result=f*factorial(f-1); // функция вызывает саму себя        return result; }

В строках 16 — 19 объявлен цикл, в котором вызывается рекурсивная функция. Всё ненужное в программе закомментировано. Запустив программу, нужно ввести значение, до которого необходимо вычислить факториалы (Рисунок 3). 

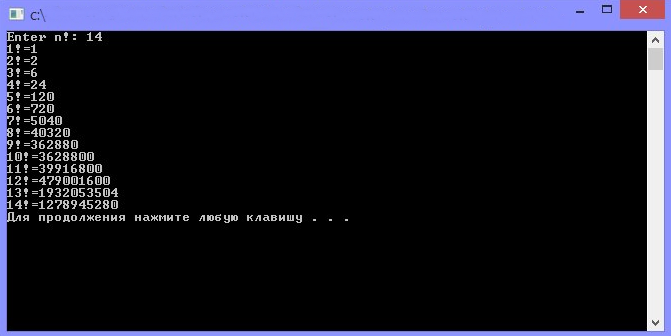
Рисунок 3. Результат работы программы.

Теперь видно, насколько быстро возрастает  факториал, кстати говоря, уже результат 14! не правильный, это и есть последствия нехватки размера типа данных.

Правильное значение 14! = 87178291200.

Лабораторное задание.

1. Написать программу в соответствии с заданием.

2. Отладить ее с применением ранее изученных средств отладки.

3. Ответить на контрольные вопросы.

4. Выполняется только один из вариантов – либо упрощенный, либо обычный.

Упрощенные варианты заданий на 5 баллов (по 10-балльной системе), когда все совсем грустно

Каждый логически завершенный фрагмент программы оформить в виде функции. Не использовать глобальные массивы переменных.

Номер варианта	Задание
1, 15	Заменить минимальный элемент данного целочисленного массива из 15 элементов на сумму предшествующих элементов, а максимальный элемент на сумму последующих элементов.
2, 16	Создать массив, состоящий из 20 целочисленных значений. Создать новый массив из номеров элементов исходного массива, имеющих нулевое значение, и сжать исходный массив, удалив все нулевые элементы.
3, 17	В массиве из 15 вещественных чисел определить, сколько раз изменяется знак и вывести номера позиций, в которых происходит смена знака.
4, 18	В массиве из 20 целых чисел найти среднее арифметическое значение элементов, попадающих во введенный с клавиатуры интервал.
5, 19	В массиве из 20 целых чисел найти сумму и количество чисел, находящихся между минимальным и максимальным элементами, включая и сами эти числа.
6, 20	Не используя других массивов переставить элементы 10-элементного символьного массива в обратном порядке.
7, 21	В массиве из 15 вещественных чисел (положительных и отрицательных) определить наибольшее количество последовательно расположенных положительных чисел.
8, 22	Создать массив из 20 символьных значений. Сформировать из его значений три других массива: состоящих из цифр, из букв и из символов, не являющихся ни буквами, ни цифрами.
9, 23	Заменить повторяющиеся элементы исходного 15-элементного массива, состоящего из целых чисел, нулевыми значениями.
10, 24	Объединить два упорядоченных по возрастанию целочисленных массива (М1[10] и M2[5]) в один, не нарушая упорядоченности.
11, 25	Дан массив int mas[15]. Создать другой массив, поместив в него сначала элементы массива, стоящие на четных местах, затем - стоящие на нечетных местах.
12, 26	Заменить нечетные элементы исходного 20-элементного массива, состоящего из целых чисел, нулевыми значениями.
13, 27	Объединить два упорядоченных по алфавиту символьных массива (М1[10] и M2[5]) в один, не нарушая упорядоченности.
14, 28	Дан массив char mas[10]. Создать другой массив, поместив в него сначала цифровые элементы массива, затем – буквенные (считаем, что в массиве содержатся только алфавитно-цифровые символы).