Физика второй семестр / Экзамен / Zadachi_na_ekzamen / 6.80-6.81_solved
.docЗанятия 21, 22.
№6.79
Найти
частное решение временного уравнения
Шредингера
для свободно движущейся частицы массы
.
Решение:
Решение уравнения будем искать в виде:
.
Подставив это выражение во временное
уравнение Шредингера с учетом того, что
частица движется свободно и
.
Получим:
,
,
получили хорошо знакомое нам дифференциальное уравнение, имеющее решение следующего вида:
,
где
,
а – некоторая постоянная. А так как
временную зависимость мы уже подобрали,
в результате получаем:
,
где
,
.
№6.80
Электрон находится
в одномерной прямоугольной потенциальной
яме с бесконечно высокими стенками.
Найти ширину ямы, если разность энергии
между уровнями с
и
составляет
.
Решение:
Чтобы вычислить длину ямы, получим сначала выражение для энергии электрона в зависимости от уровня, на котором он находится. Рассмотрим уравнение Шредингера внутри ямы:
.
По условию, внутри ямы
,
тогда примем
и с учетом одномерности запишем:
.
Для решения этого дифференциального
уравнения, проведем аналогию с уравнениями
вида
,
для которых решение следует искать в
виде
,
тогда
.
Рассмотрим две граничные точки, в которых волновая функция ввиду ее непрерывности должна быть равна нулю:
:
;
:
.
Вспоминаем, что в наших обозначениях , тогда
.
.
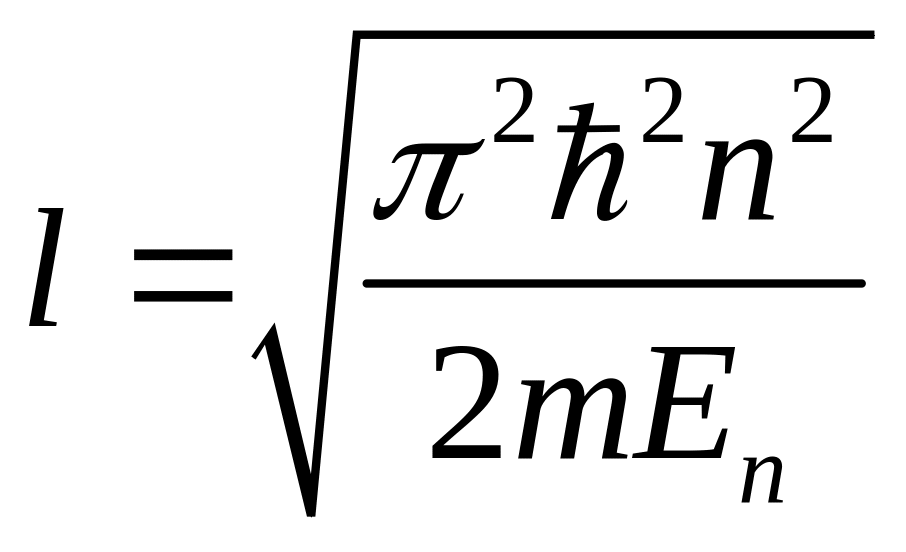№6.81
Частица
находится в основном состоянии в
одномерной прямоугольной потенциальной
яме ширины l
с абсолютно
непроницаемыми стенками (
).
Найти вероятность пребывания частицы
в области
.
Решение:
Согласно физическому
смыслу
-функции,
вероятность нахождения частицы в
элементарном объеме
описывается выражением:
.
Наша задача – получить решение уравнение Шредингера для частицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Запишем уравнение Шредингера:
.
С учетом того, что в яме потенциальная энергия частицы = 0, запишем:
.
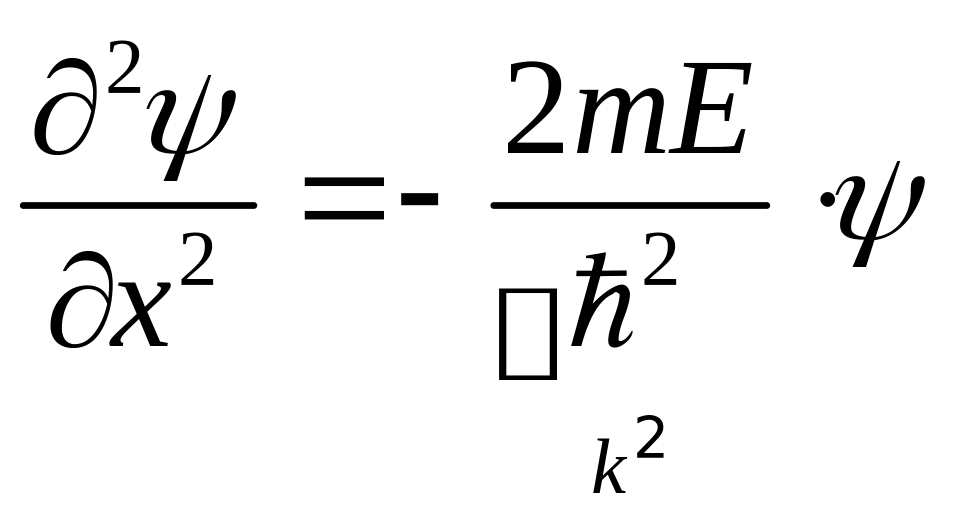
Решение последнего дифференциального уравнения нужно искать в виде:
.
Рассмотрим два граничных условия:
1) т.к. при
;
2) т.к. при
,
имеем:
,
причем
,
т.к. получится, что частицы нет ни внутри
ямы, ни за ее пределами. Значит, волновая
функция имеет вид:
.
Найдем константу
.
Из условий нормировки получим:
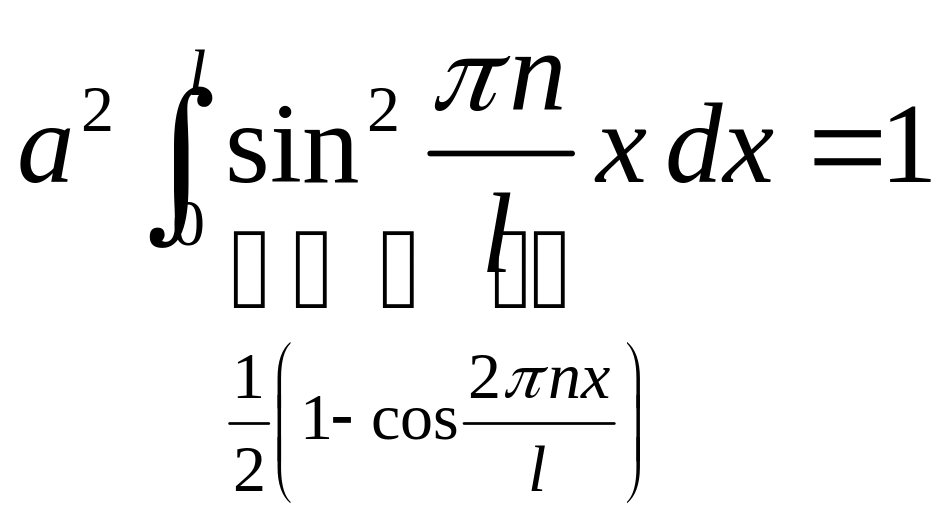
Таким образом, собственные функции имеют вид:
.
Теперь чтобы найти вероятность нахождения частицы в заданной области, нужно просто взять определенный интеграл:
.
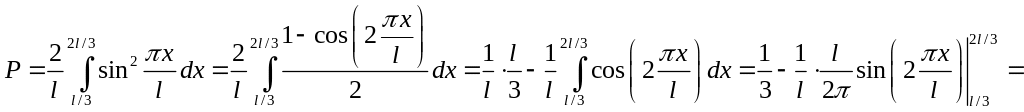
№6.82 Частица находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы l. Найти нормированные волновые функции стационарных состояний частицы, взяв начало отсчета координаты х в середине ямы.
Р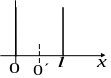
ешение:
Как
известно (см. задачу 6.81), пси-функция
частицы, находящейся в одномерной
прямоугольной потенциальной яме с
бесконечно высокими стенками, если
начало координат совпадает с одной из
границ ямы, выглядит следующим образом:
.
Очевидна замена переменной – переход к «штрихованной» системе отсчета, где за начало отсчета принята середина ямы:
.
Отсюда легко можно получить выражение для пси-функции в новой системе отсчета:
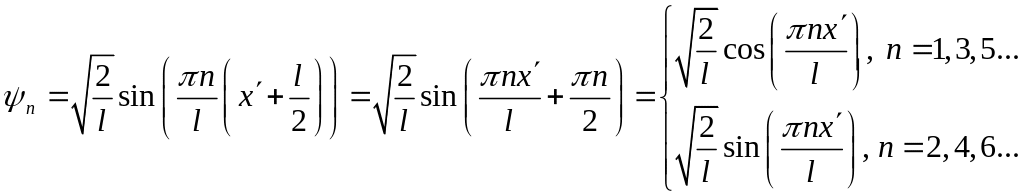
На самом деле, при четных и нечетных n
будет наблюдаться чередование знака
соответственно перед синусом и косинусом.
Но, как известно, пси-функция определена
с точностью до множителя, модуль которого
= 1, т.е. домножение на
(равно как и на
,
или на
)
роли не играет.
№6.85 Частица массы m находится в двумерной прямоугольной потенциальной яме с абсолютно непроницаемыми стенками. Найти:
а) возможные
значения энергии частицы, если стороны
ямы равны
,
;
б) значения энергии
частицы на первых четырех уровнях, если
яма квадратная со стороной
.
Решение: а) Запишем уравнение Шредингера:
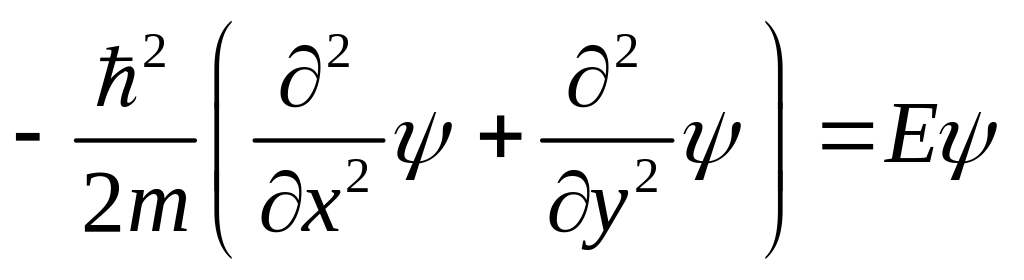
Будем искать решение этого уравнения
в виде
.
Из условий
следует, что начальные фазы синусов
равны нулю. Убеждаемся, что это выражение
действительно является решением
уравнения Шредингера. После подстановки
и сокращения на
,
получим:
.
Снова обратимся к условию непрерывности -функции на границе ямы:
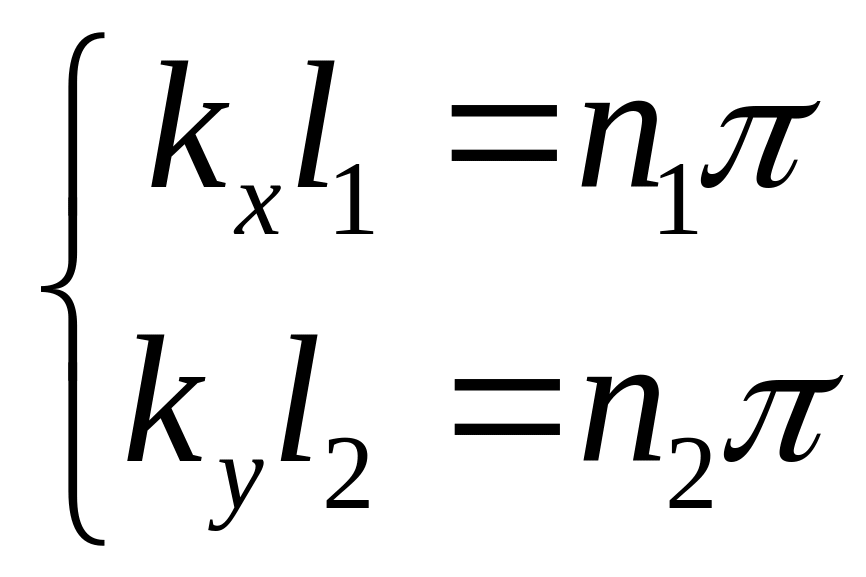
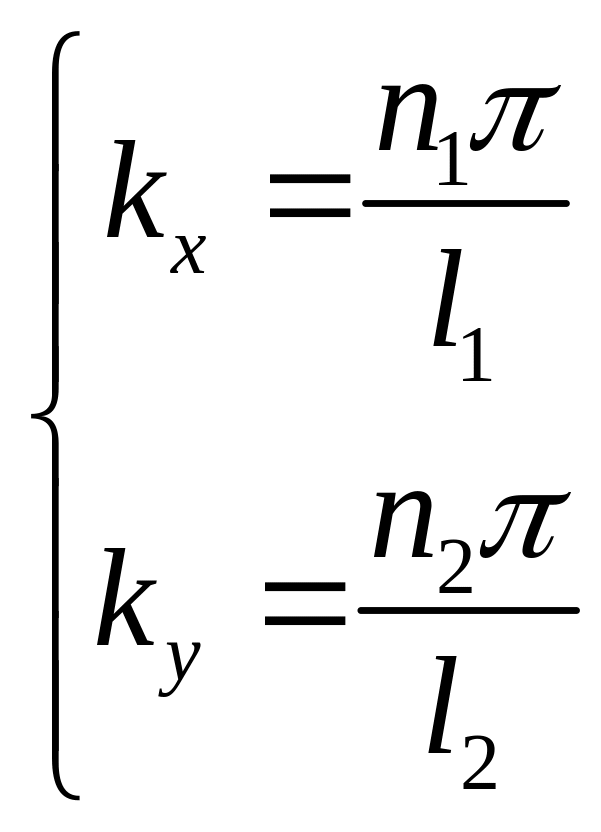
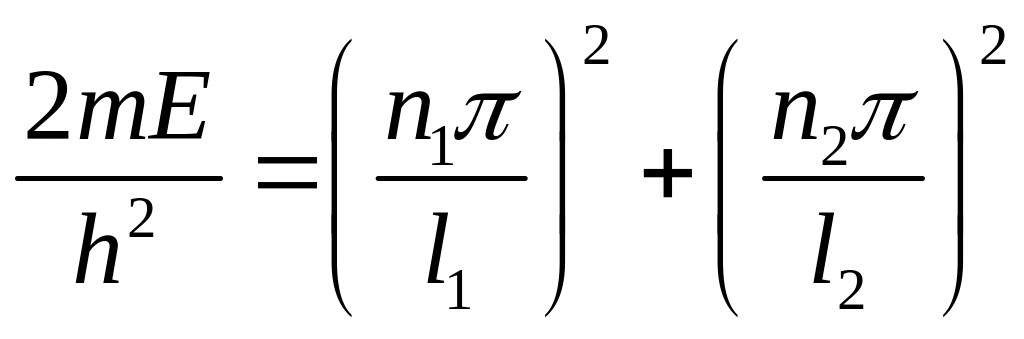
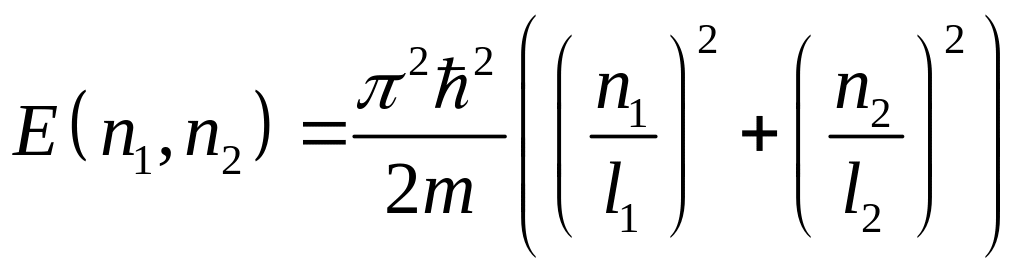
б) Если яма квадратная со стороной l, то последнее выражение для энергии, полученное в пункте а) приобретает вид:
.
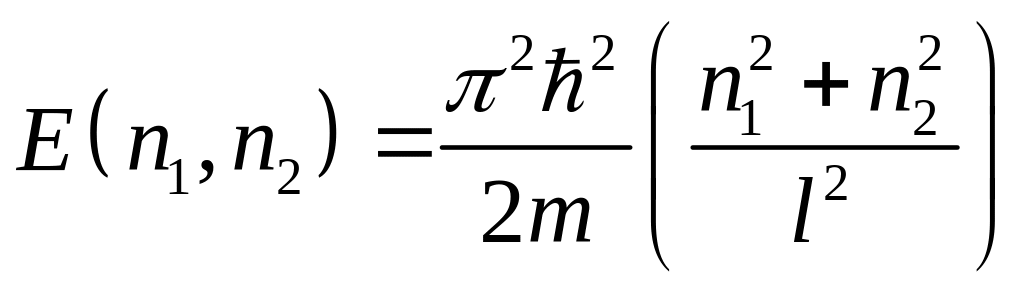Т.к. частица находится в потенциальной
яме,
.
Тогда:
;
,
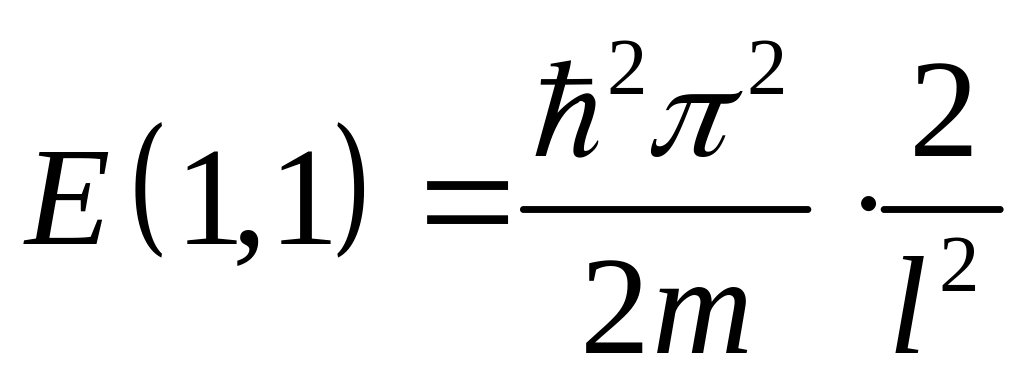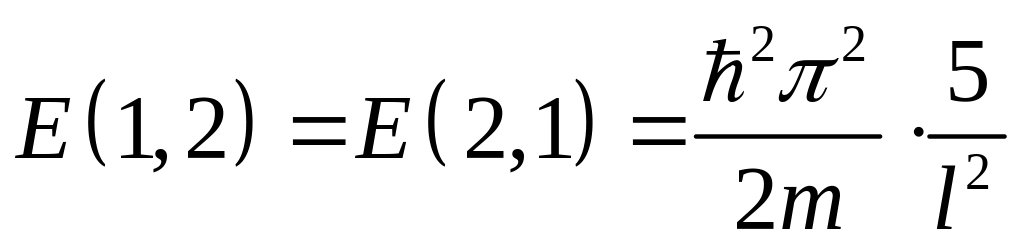однако это будут два различных состояния,
поскольку они описываются двумя
различными
-функциями!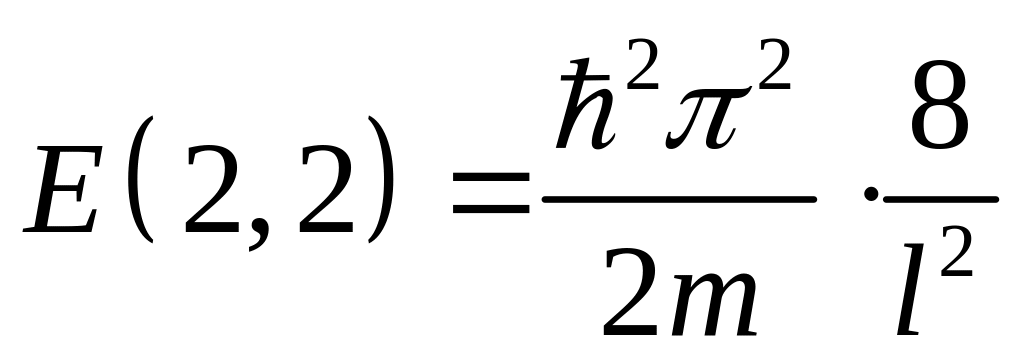
; 
.
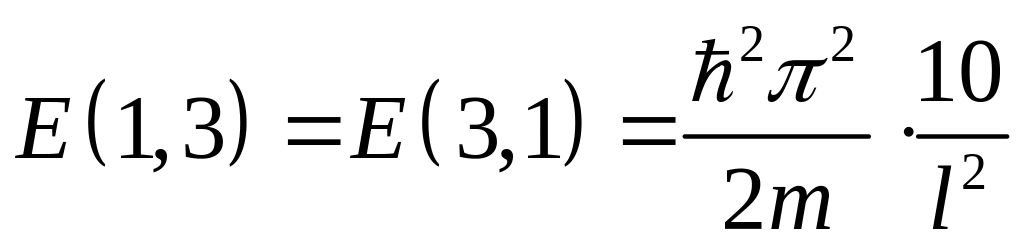Замечание: Очевидно, на границе потенциальной ямы нарушается условие гладкости пси-функции:
,
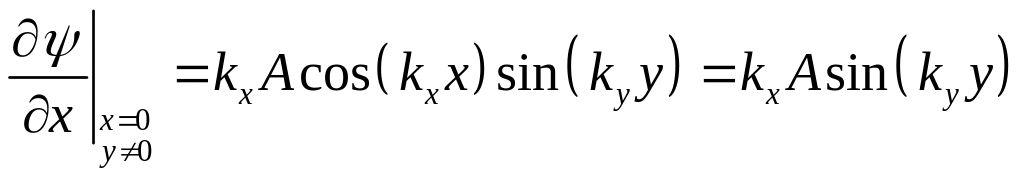т.е. по идее, вне ямы производная пси-функции (которая тождественно = 0) равна нулю, а на границе равна некоторой константе. Дело в том, что потенциальная яма с бесконечно высокими стенками есть некая идеализация, на практике не осуществимая. В случае потенциальной ямы со сколь угодно высокими, но не бесконечно высокими стенками условие гладкости будет выполняться.
№6.92
Найти
возможные значения энергии частицы
массы
,
находящейся в сферически-симметричной
потенциальной яме
при
и
,
для случая, когда движение частицы
описывается волновой функцией
,
зависящей только от
.
Решение:
Запишем уравнение Шредингера:
,
поскольку сказано, что в яме
.
Воспользуемся
выражением лапласиана в полярных
координатах:
.
Теперь в соответствие с указанием
воспользуемся подстановкой
:
.
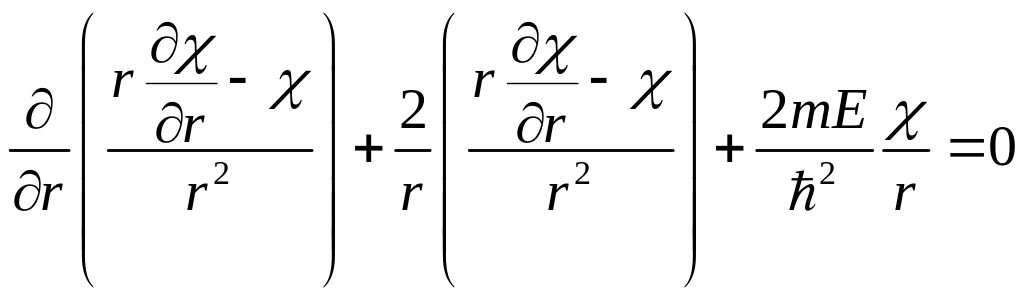Сделав замену
и продолжая выкладки, получим:
.
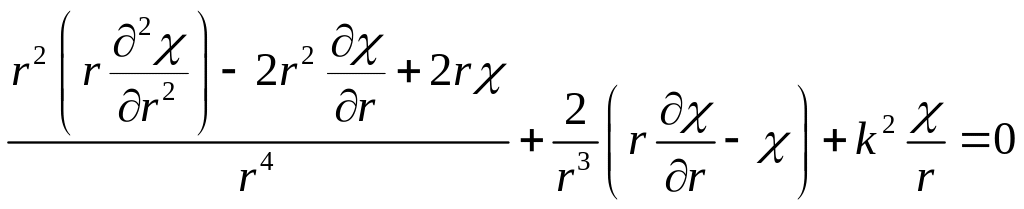
Решение этого дифференциального
уравнения будем искать в виде
,
т.е.
. Из условия конечности функции в точке
следует, что
.
Из условия
,
Вспоминаем, что такое
:
№6.95
Волновая
функция частицы массы m
для основного состояния в одномерном
потенциальном поле
имеет вид
,
где A
и
– некоторые постоянные. Найти с помощью
уравнения Шредингера постоянную
и энергию E
частицы в этом состоянии.
Решение:
Запишем уравнение Шредингера с учетом того, что яма одномерная:
.
Подставим сюда выражение для , которое нам дано по условию:
.
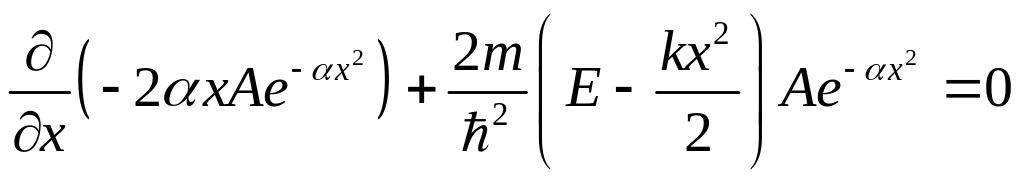
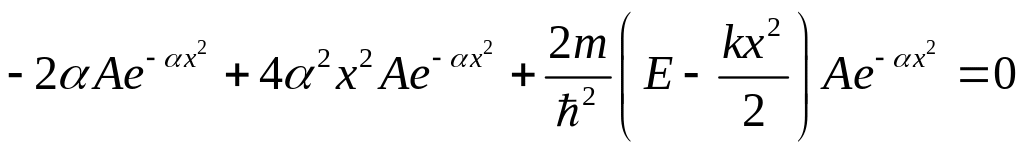
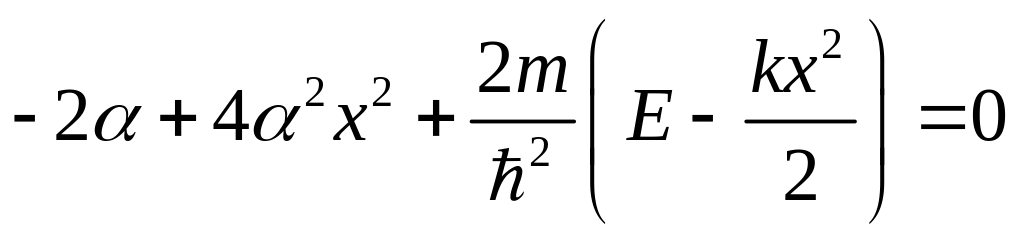
Теперь вспоминаем, что энергия частицы
в потенциальном поле – величина
дискретная, не зависящая от
,
тогда из последнего выражения получаем:
.
Введя обозначение
,
получим, что
.
Теперь можно найти выражение для энергии
частицы в этом состоянии:
.
№6.96
Определить
энергию электрона атома водорода в
состоянии, для которого волновая функция
имеет вид
,
где A,
a
и
– некоторые постоянные.
Решение:
Запишем уравнение Шредингера:
.
Воспользуемся выражением лапласиана в полярных координатах:
.
Поделим все выражение на
и учтем, что
- энергия взаимодействия электрона с
ядром, получим:
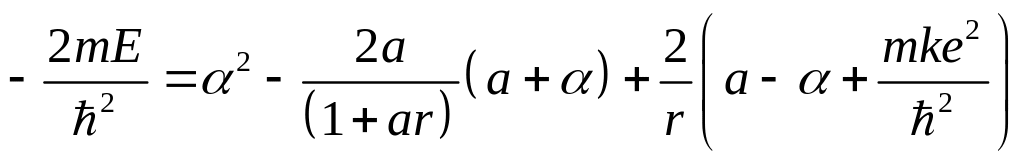
Энергия частицы в потенциальном поле
– величина дискретная, не зависящая от
,
тогда из последнего выражения получаем:
.
Найдем из системы уравнений выше величину
:
,
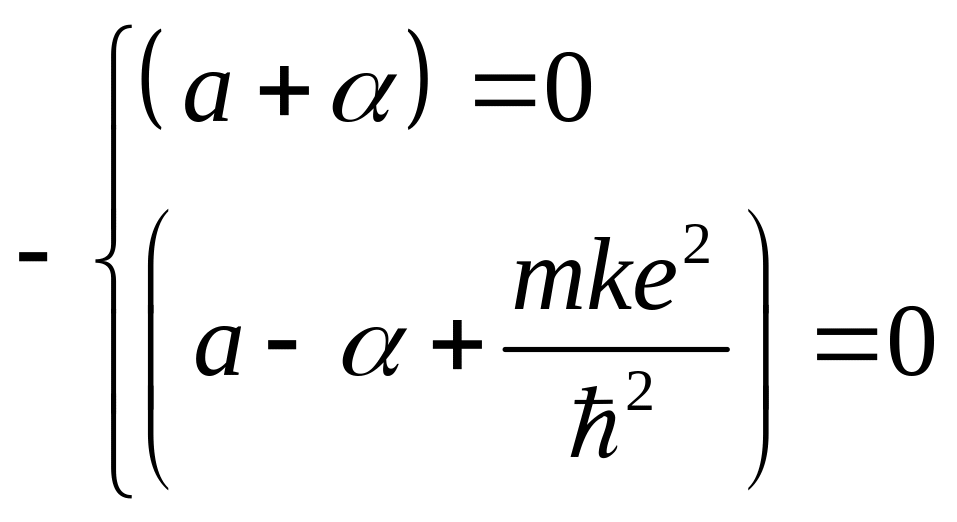
тогда искомая энергия электрона равна:
.
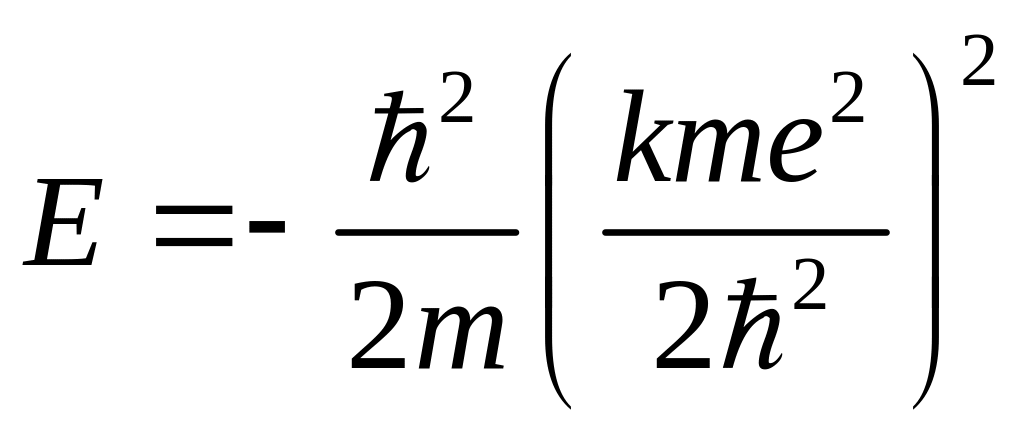
№6.97
Волновая
функция электрона в основном состоянии
атома водорода имеет вид
,
где
- некоторая постоянная,
- первый боровский радиус. Найти:
а) наиболее вероятное расстояние между электроном и ядром;
б) среднее значение модуля кулоновской силы, действующей на электрон;
в) среднее значение потенциальной энергии электрона в поле ядра.
Решение:
а) Как известно, вероятность нахождения частицы в элементарном объеме определяется выражением:
,
где в нашем случае
- элементарный шаровой слой, тогда
.
Таким образом, чтобы найти наиболее вероятное расстояние между электроном и ядром, нам нужно найти максимум функции, отвечающей за плотность вероятности того факта, что частица находится на расстоянии от ядра:
,
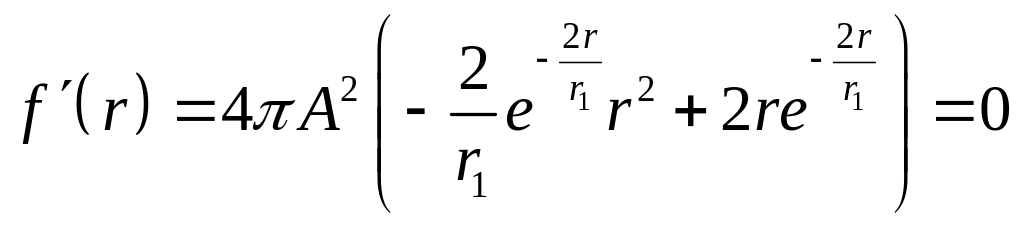
т.к. нас интересует максимум функции.
б) Как известно, среднее значение
некоторой величины
в состоянии, описываемом некоторой
функцией
,
может быть вычислено по формуле
,
тогда, т.к.
,
.
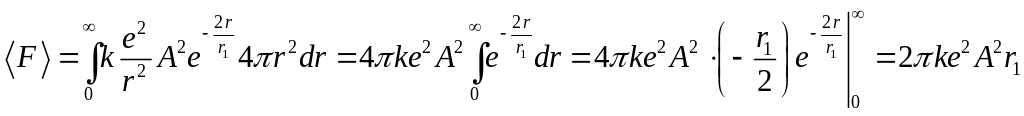Константу
определим из условия нормировки
-функции:
.
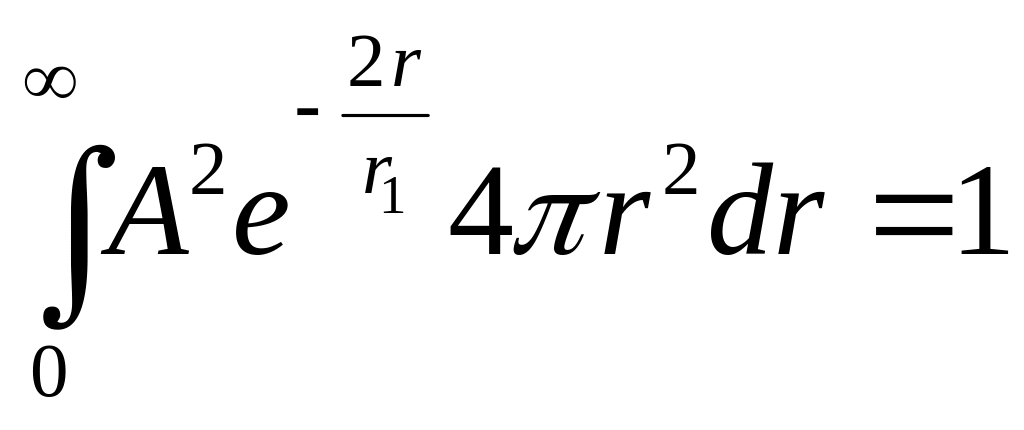
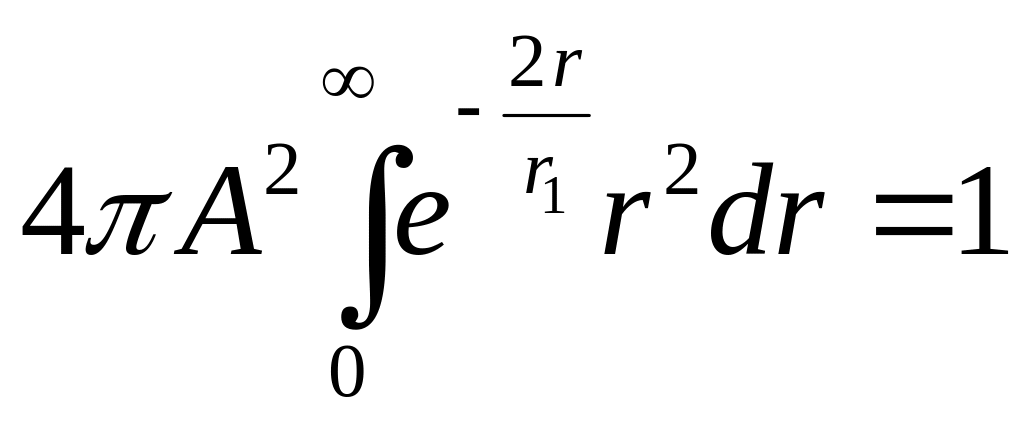
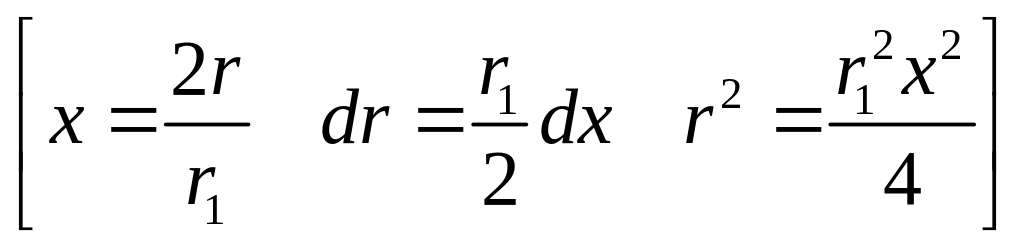
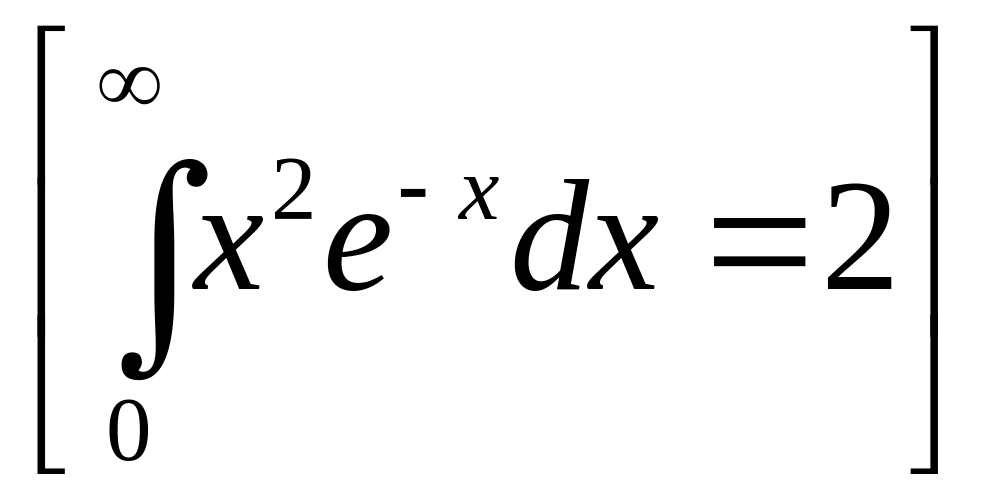
в) Аналогично поступаем с потенциальной
энергией электрона в поле ядра
:
=
.
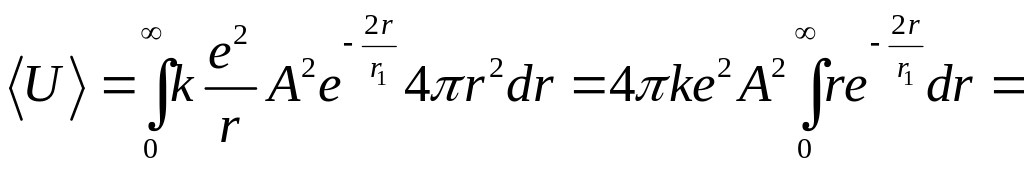
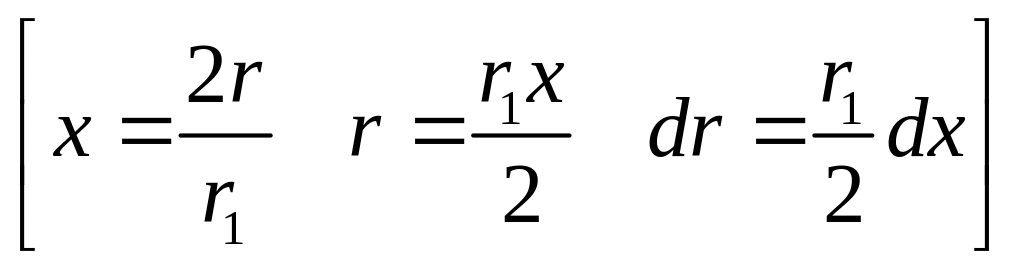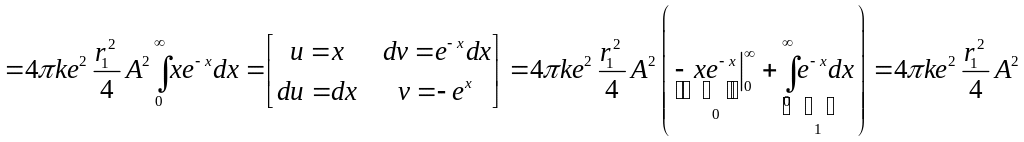Подставив уже известное А, получим:
.
№
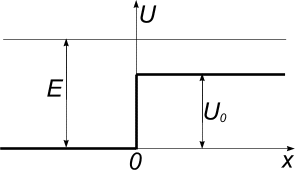6.102
Частицы
массой
и энергией
движутся слева на потенциальный барьер
(см рис.). Найти:
а) коэффициент
отражения
этого барьера при
;
б) эффективную
глубину проникновения частиц в область
при
,
т.е. расстояние от границы барьера до
точки, где плотность вероятности
нахождения частицы уменьшается в
раз.
Решение:
а) Запишем уравнение Шредингера для
этой частицы до и после барьера, учитывая,
что ее потенциальная энергия до барьера
равна 0, а после барьера -
:
и 
Будем искать решения уравнения вида:
.
Подставим в уравнение Шредингера, тогда
.
и
.
Из этих уравнений получим соответственно:
(учитывая
что энергия движущейся частицы
положительна и корень извлекается из
отрицательного числа) и
(учитывая, что в первом случае
и корень извлекается из отрицательного
числа). Тогда решения уравнений будут
выглядеть так:
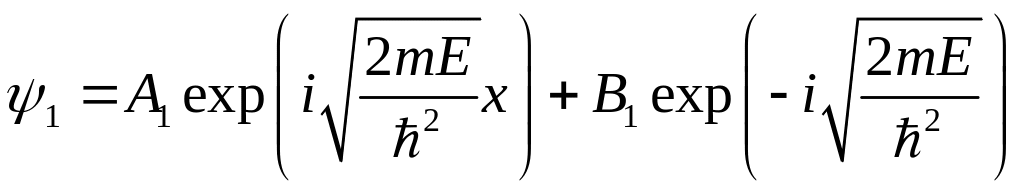
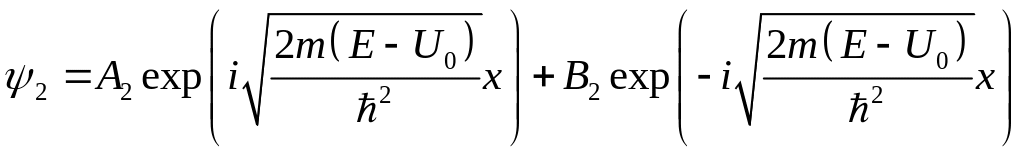
Частицы отражаются от барьера, значит
,
но в барьере они движутся только в
положительном направлении, тогда
.
Из условия непрерывности волновой
функции на границе получаем:
(1)