
- •Модуль 2 волновая и квантовая оптика задачи и тесты на первую контрольную и экзамен по поляризации света
- •2) Интенсивность света на выходе из первого поляризатора (р) равна ;
- •4) Интенсивность света на выходе из второго поляризатора (а) равна .
- •Указание см. Материал лекции (модуль 2. Тема 3. ) Поляризация света при отражении и преломлении. Закон Брюстера
- •2. Изменение фазы колебаний при отражении.
- •См. Материал лекции: Поляризация световых волн
2. Изменение фазы колебаний при отражении.
Если угол падения
α1<αБр,
то амплитудные коэффициенты отражения
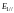 и
и
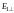 отрицательны (см. формулы (3). Это означает,
что фаза колебаний напряженности
электрического поля изменяется при
отражении на ,
что эквивалентно «потере /2».
Если фаза меняется на ,
то отраженная волна проходит как бы
лишний путь, равный /2.
Направим ось x
вдоль отраженного луча. Тогда:
отрицательны (см. формулы (3). Это означает,
что фаза колебаний напряженности
электрического поля изменяется при
отражении на ,
что эквивалентно «потере /2».
Если фаза меняется на ,
то отраженная волна проходит как бы
лишний путь, равный /2.
Направим ось x
вдоль отраженного луча. Тогда:
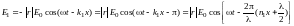 ,
,
где
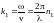 ,
n1x
- оптический
путь отраженной волны от границы раздела
до плоскости с координатой x.
,
n1x
- оптический
путь отраженной волны от границы раздела
до плоскости с координатой x.
Отмеченное обстоятельство с изменением фазы на при отражении крайне важно в явлениях интерференции, для физики и технологии диэлектрических покрытий при изготовлении интерференционных зеркал и светофильтров.
Отметим, что фаза колебаний магнитного поля в этом случае не меняется.
ЗАДАЧИ
4.181 [5.172]
Пучок естественного света падает на систему из N=6 поляризаторов, плоскость пропускания каждого из которых повернута на угол =30 относительно плоскости пропускания предыдущего поляризатора. Какая часть светового потока проходит через эту систему ?
4.183 [5.174]
Степень поляризации
частично поляризованного света
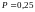 .
Найти отношение интенсивности
поляризованной составляющей этого
света к интенсивности естественной
составляющей.
.
Найти отношение интенсивности
поляризованной составляющей этого
света к интенсивности естественной
составляющей.
ЗАДАЧА СРС ( Задано на лекции) ОЗНАКОМИТЬСЯ С РЕШЕНИЕМ
Плоскополяризованный свет падает на стеклянную пластинку под углом Брюстера. Колебания напряженности электрического поля происходят в плоскости падения. Покажите, что такой свет проходит через пластинку без отражения.
Решение: Схема
прохождения света через пластинку
показана на
рис.2 (см. выше).
При падении под углом Брюстера
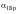 отражение от верхней поверхности
отсутствует. Угол преломления α2
является в этом случае углом Брюстера
при падении на нижнюю поверхность
пластинки. Действительно, луч 3 параллелен
лучу 1, и сумма углов падения и преломления
на нижнюю поверхность пластинки равна
π/2. Кроме того, из закона преломления
отражение от верхней поверхности
отсутствует. Угол преломления α2
является в этом случае углом Брюстера
при падении на нижнюю поверхность
пластинки. Действительно, луч 3 параллелен
лучу 1, и сумма углов падения и преломления
на нижнюю поверхность пластинки равна
π/2. Кроме того, из закона преломления
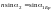 следует
следует
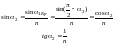
Угол
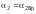 ,
значит отражения нет и от нижней
поверхности.
,
значит отражения нет и от нижней
поверхности.
Отмеченное свойство нашло, например, применение при изготовлении газовых лазеров. Газоразрядная трубка лазера на торцах имеет стеклянные пластинки, установленные под углом Брюстера к ее оси, для уменьшения потерь на отражения для света, поляризованного в плоскости падения.
4.190 [5.180]
Естественный свет падает под углом Брюстера на поверхность стекла. Определить с помощью формул Френеля:
а) коэффициент отражения;
б) степень поляризации преломлённого света.
ОЗНАКОМИТЬСЯ С РЕШЕНИЕМ
4.178 [5.169]
Плоская монохроматическая
волна естественного света с интенсивностью
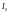 падает нормально на круглое отверстие,
которое представляет собой первую зону
Френеля для точки наблюдения Р. Найти
интенсивность света в точке Р после
того, как отверстие перекрыли двумя
одинаковыми поляризаторами, плоскости
пропускания которых взаимно перпендикулярны,
а граница их раздела проходит:
падает нормально на круглое отверстие,
которое представляет собой первую зону
Френеля для точки наблюдения Р. Найти
интенсивность света в точке Р после
того, как отверстие перекрыли двумя
одинаковыми поляризаторами, плоскости
пропускания которых взаимно перпендикулярны,
а граница их раздела проходит:
а) по диаметру отверстия;
б) по окружности, ограничивающей первую половину зоны Френеля.
Решение:
а )
Как известно,
интенсивность естественного света,
прошедшего через поляризатор, становится
равной
)
Как известно,
интенсивность естественного света,
прошедшего через поляризатор, становится
равной
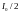 ;
соответственно, амплитуда становится
равной
;
соответственно, амплитуда становится
равной
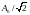 .
Поскольку отверстие перекрыто по
диаметру, в образовании дифракционной
картины будет принимать участие вся
первая зона Френеля. Поляризатор,
перекрывающий правую часть отверстия
(см. рисунок), даст
.
Поскольку отверстие перекрыто по
диаметру, в образовании дифракционной
картины будет принимать участие вся
первая зона Френеля. Поляризатор,
перекрывающий правую часть отверстия
(см. рисунок), даст
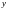 -вклад
в образование результирующей амплитуды,
причем амплитуда этого вклада равна,
как следует из рисунка,
.
Поляризатор, перекрывающий левую часть
отверстия, даст точно такой же
-вклад
в образование результирующей амплитуды,
причем амплитуда этого вклада равна,
как следует из рисунка,
.
Поляризатор, перекрывающий левую часть
отверстия, даст точно такой же
 -вклад
в образование результирующей амплитуды,
тогда
-вклад
в образование результирующей амплитуды,
тогда
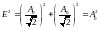
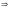
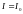 .
■
.
■
б )
Поскольку
отверстие перекрыто по окружности,
ограничивающей первую половину зоны
Френеля, в образовании
)
Поскольку
отверстие перекрыто по окружности,
ограничивающей первую половину зоны
Френеля, в образовании
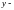 составляющей
результирующей амплитуды будет принимать
участие первая половина первой зоны
Френеля, в образовании
составляющей
результирующей амплитуды будет принимать
участие первая половина первой зоны
Френеля, в образовании
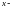 составляющей
– вторая половина. Как следует из
рисунка, амплитуды составляющих:
составляющей
– вторая половина. Как следует из
рисунка, амплитуды составляющих:
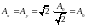 .
.
И опять же эти составляющие перпендикулярны, поскольку перпендикулярны плоскости пропускания поляризаторов. Тогда для результирующей амплитуды имеем:
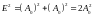
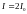 .
■
.
■
[5.191] (Расчетное задание к лаб работам)
Какой характер
поляризации имеет плоская электромагнитная
волна, проекции вектора
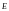 которой на оси х и у, перпендикулярные
к направлению ее распространения,
определяются следующими уравнениями:
которой на оси х и у, перпендикулярные
к направлению ее распространения,
определяются следующими уравнениями:
а)
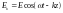 ,
,
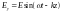 ;
;
б)
,
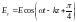 ;
;
в)
,
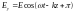 .
.
УКАЗАНИЕ
