
- •Модуль 2 волновая и квантовая оптика задачи и тесты на первую контрольную и экзамен по поляризации света
- •2) Интенсивность света на выходе из первого поляризатора (р) равна ;
- •4) Интенсивность света на выходе из второго поляризатора (а) равна .
- •Указание см. Материал лекции (модуль 2. Тема 3. ) Поляризация света при отражении и преломлении. Закон Брюстера
- •2. Изменение фазы колебаний при отражении.
- •См. Материал лекции: Поляризация световых волн
Модуль 2 волновая и квантовая оптика задачи и тесты на первую контрольную и экзамен по поляризации света
Т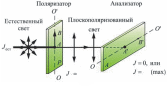 ЕСТЫ
ЕСТЫ
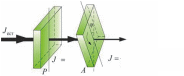
1. Рассмотрите рисунок.
На
первый поляризатор падает естественный
свет интенcивности
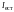 .
Направление пропускания поляризаторов
взаимоперпендикулярны.
.
Направление пропускания поляризаторов
взаимоперпендикулярны.
После прохождения двух поляризаторов интенсивность света I равна:
1)
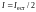 ;
2)
;
2)
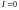 ;
;
3)
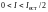 ; 4)
; 4)
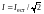
2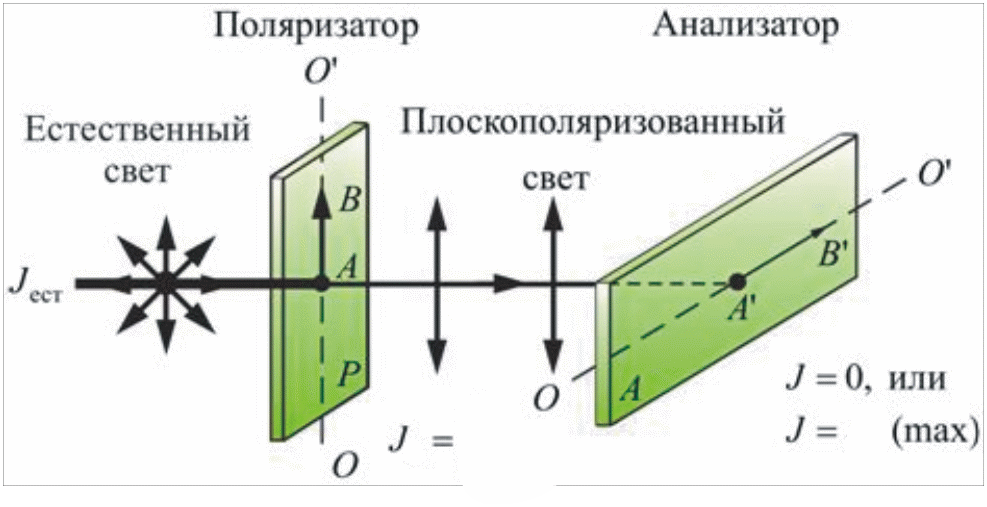
 .
Рассмотрите рисунок. На первый поляризатор
падает естественный свет интенcивности
.
Найдите правильные утверждения:
.
Рассмотрите рисунок. На первый поляризатор
падает естественный свет интенcивности
.
Найдите правильные утверждения:
1)
Интенсивность света на выходе из первого
поляризатора (Р) равна
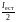 ;
;
2) Интенсивность света на выходе из первого поляризатора (р) равна ;
3) Интенсивность света на выходе из второго поляризатора (А) равна ;
4) Интенсивность света на выходе из второго поляризатора (а) равна .
3.
Степень поляризации
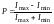 для плоскополяризованного света равна:
для плоскополяризованного света равна:
1).
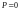 . 2).
. 2).
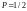 . 3).
. 3).
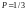 . 4).
. 4).
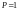
4. Степень поляризации для естественного света равна:
1). . 2). . 3). . 4).
5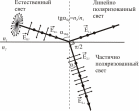 .
(СМ. УКАЗАНИЕ НИЖЕ)
При падении света из воздуха на диэлектрик
отраженный свет полностью поляризован.
Угол преломления равен 30о.
Тогда показатель преломления диэлектрика
равен
.
(СМ. УКАЗАНИЕ НИЖЕ)
При падении света из воздуха на диэлектрик
отраженный свет полностью поляризован.
Угол преломления равен 30о.
Тогда показатель преломления диэлектрика
равен
1)
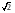
2)
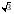
3) 1,5
4)2,0
Указание см. Материал лекции (модуль 2. Тема 3. ) Поляризация света при отражении и преломлении. Закон Брюстера
Пусть плоская
световая волна падает на границу раздела
двух оптических немагнитных сред с
показателями преломления
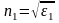 и
и
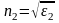 (рис.1).
(рис.1).
Д
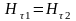
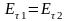
, (1)
где индекс относится к тангенциальным (параллельным границе) составляющим напряженностей. Кроме того, уравнения Максвелла дают общее выражение, связывающее напряженности электрического и магнитного полей в плоской волне.
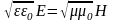
(свойство синфазности
колебаний
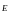 и
и
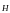 ) (2)
) (2)
Н
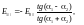
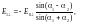
(3)

Формулы (3) следуют
из граничных условий (1) с учетом (2) и
закона преломления
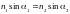 .
.
Интенсивность I
пропорциональна среднему значению
квадрата напряженности
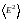 .
Возводя в квадрат соотношения (3) и
усредняя, можно записать формулы Френеля
для интенсивностей отраженного и
преломленного света.
.
Возводя в квадрат соотношения (3) и
усредняя, можно записать формулы Френеля
для интенсивностей отраженного и
преломленного света.
Из (3) следует, что
плоско-поляризованная волна, в которой
напряжённость электромагнитного поля
колеблется в плоскости падения, не
отражается от границы раздела оптических
сред, если
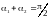 ,
так как
,
так как
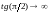 (рис. 2). Угол падения
(рис. 2). Угол падения
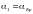 в этом случае называется углом
Брюстера. Из
закона преломления следует:
в этом случае называется углом
Брюстера. Из
закона преломления следует:
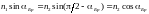 ,
или
,
или
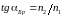
(4)
Основные закономерности, вытекающие из формул Френеля:
1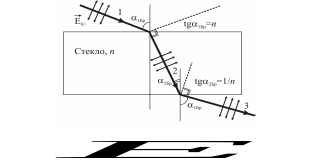 .
Закон Брюстера.
Если на границу раздела двух оптических
сред падает естественный
свет под углом Брюстера,
когда
.
Закон Брюстера.
Если на границу раздела двух оптических
сред падает естественный
свет под углом Брюстера,
когда
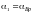 ,
,
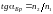 ,
то отраженный
свет полностью поляризован так,
что колебания напряженности электрического
поля происходят перпендикулярно
плоскости падения. Преломленный
свет оказывается
частично
поляризованным.
Угол между
отраженным и
преломленным лучом составляет /2,
то есть
,
то отраженный
свет полностью поляризован так,
что колебания напряженности электрического
поля происходят перпендикулярно
плоскости падения. Преломленный
свет оказывается
частично
поляризованным.
Угол между
отраженным и
преломленным лучом составляет /2,
то есть
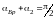 (рис.2).
(рис.2).
