Физика второй семестр / Экзамен / Zadachi_na_ekzamen / 3_Difraktsia_Zadachi_Na_Pervuyu_Kontrolnuyu_I_Ekzamen
.docxМОДУЛЬ 2 ВОЛНОВАЯ И КВАНТОВАЯ ОПТИКА
ЗАДАЧИ НА ПЕРВУЮ КОНТРОЛЬНУЮ И ЭКЗАМЕН
ПО ДИФРАКЦИИ СВЕТА
1. ДИФРАКЦИЯ НА ЩЕЛИ
см. лекция, семинар, файл "Оптика в рисунках"
4.133 [5.124]
Свет
с длиной волны
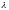 падает нормально на длинную прямоугольную
щель ширины
падает нормально на длинную прямоугольную
щель ширины
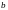 .
Найти угловое распределение интенсивности
света при фраунгоферовской дифракции,
а также угловое положение минимумов.
.
Найти угловое распределение интенсивности
света при фраунгоферовской дифракции,
а также угловое положение минимумов.
Указание : Решите задачу, используя принцип Гюйгенса-Френеля и метод векторных диаграмм
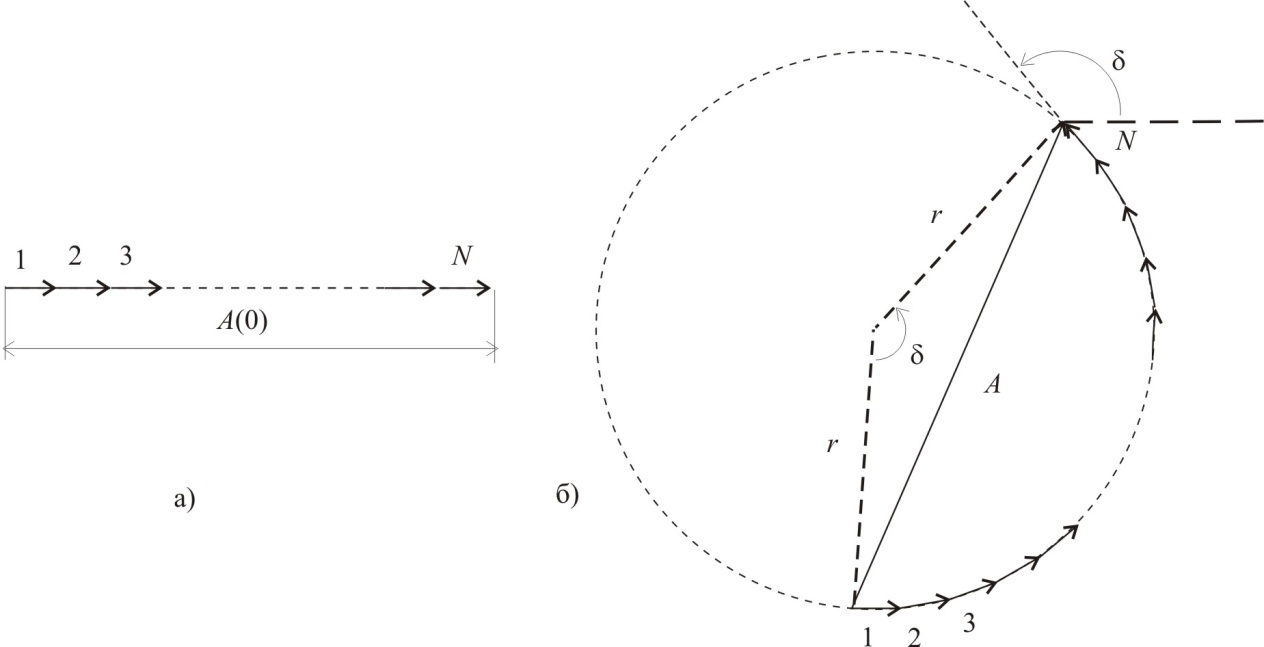
ЛИЧНО ПОЛУЧИТЬ!
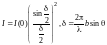
ТЕСТ На рис. 1-4 показаны векторные диаграммы для дифракции Фраунгофера на щели
при различных углах дифракции. Длина векторной «цепочки» на всех рисунках одинакова.
Рис. № |
1 |
2 |
3 |
4 |
|
|
|
|
|
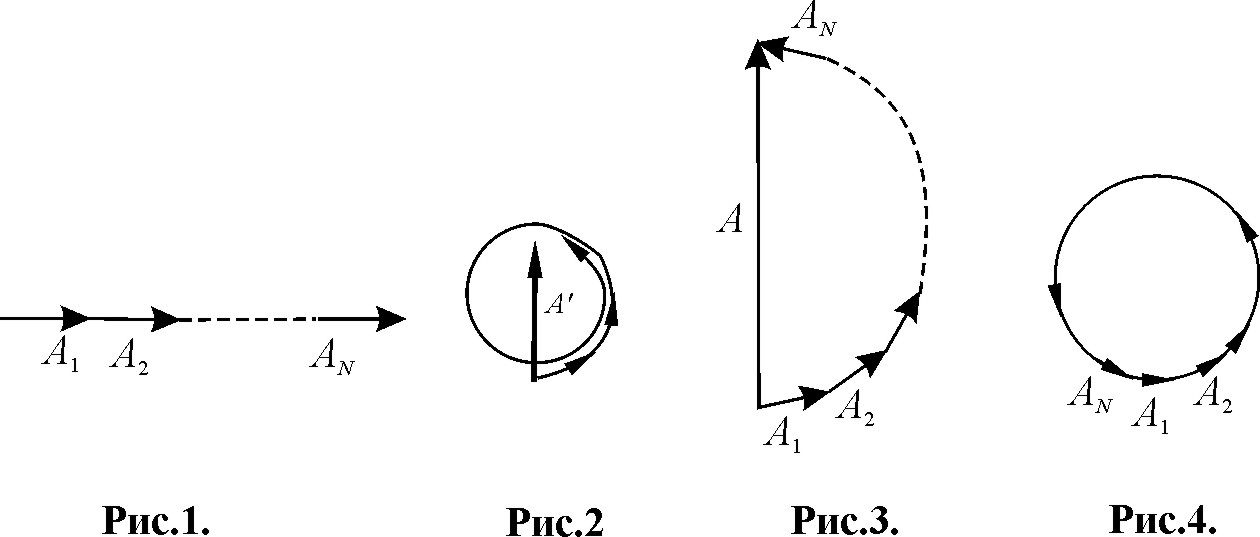
Поставьте в соответствие рисункам значение
4.134 [5.125]
Монохроматический свет падает нормально на щель ширины b=11 мкм. За щелью находится тонкая линза с фокусным расстоянием f=150 мм, в фокальной плоскости которой расположен экран. Найти длину волны света, если расстояние между симметрично расположенными минимумами третьего порядка (на экране) равно x=50 мм.
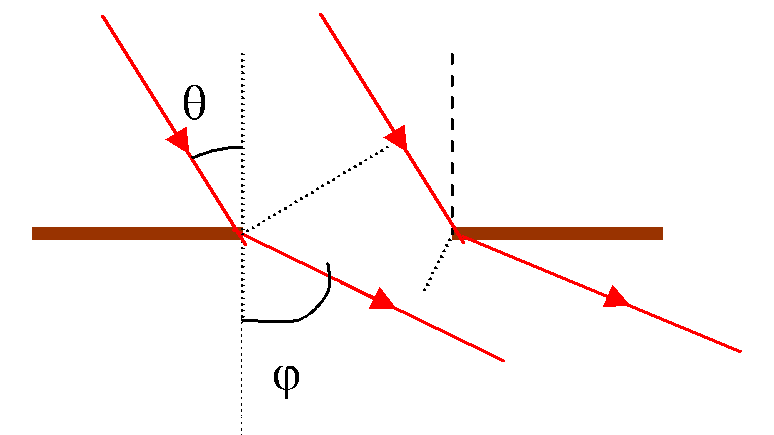
Наклонное падение света на решетку файл "Оптика в рисунках"
Если рассмотреть наклонное падение волны на дифракционную решетку, то разность хода между крайними
точками
равна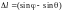 отсюда условие минимумов
отсюда условие минимумов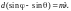 ,
,
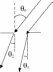
4.135 [5.126]
Свет
с длиной волны
=0,50
мкм падает на щель ширины
=10
мкм под углом
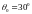 к её нормали. Найти угловое положение
первых минимумов, расположенных по обе
стороны центрального фраунгоферова
максимума.
к её нормали. Найти угловое положение
первых минимумов, расположенных по обе
стороны центрального фраунгоферова
максимума.
ТЕСТ
На
рисунке представлена картина распределение
интенсивности при дифракции света на
щели (нормальное падение). Чему равно
значение
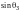 для 3-го минимума (ширина щели – b,
для 3-го минимума (ширина щели – b,
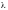 - длина волны падающего света):
- длина волны падающего света):
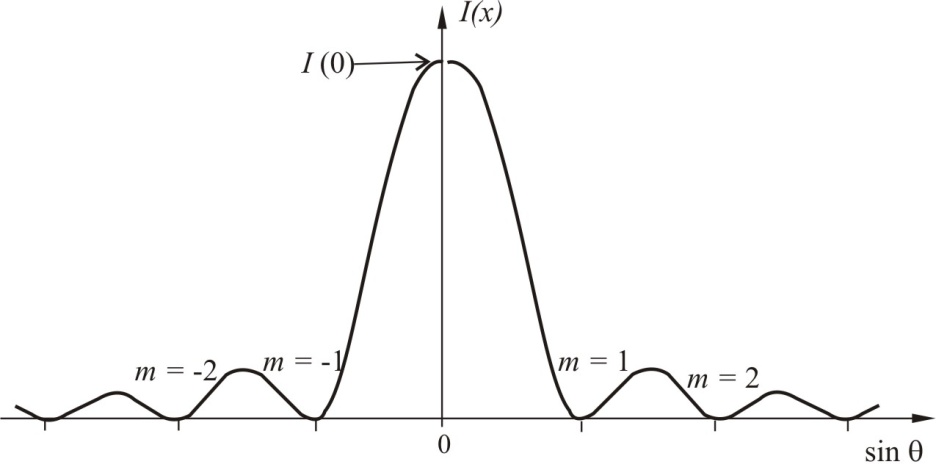
1).
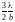 ; 2.
; 2.
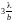 ;
3.
;
3.
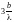 ;
4.
;
4.
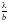 .
.
2. ДИФРАКЦИЯ НА РЕШЕТКЕ
Тест
Тест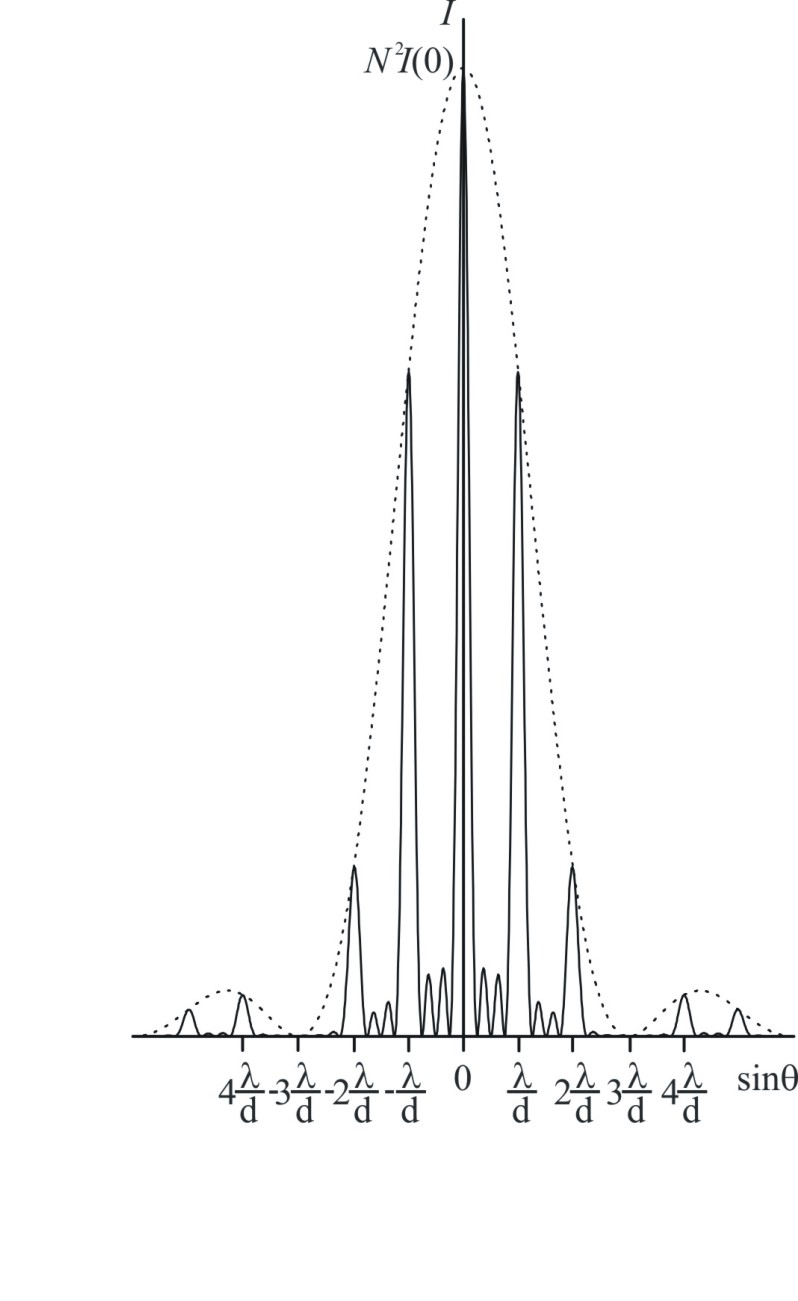
Найдите отношение
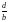 :
:
1) 2; 1) 3; 1) 4; 1) 9.
4.138 [5.129]
Изобразить
примерную дифракционную картину,
возникающую при дифракции Фраунгофера
от решётки от
трёх одинаковых
щелей, если отношение периода решётки
к ширине щели
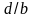 равно
равно
а) двум; б) трём.
4.139 [5.130]
При нормальном падении света на дифракционную решетку угол дифракции для линии 1=0,65 мкм во втором порядке равен 45. Найти угол дифракции для линии 2=0,50 мкм в третьем порядке.
СПЕКТРАЛЬНЫЕ ХАРАКТЕРИСТИКИ РЕШЕТКИ
см. лекция, файл "Оптика в рисунках"
Угловая дисперсия
Угловой дисперсией спектральных приборов называется величина
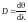
В случае решетки, угловая дисперсия равна
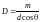
Приближенное
выражение
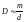 справедливо
в случае малых дифракционных углов.
справедливо
в случае малых дифракционных углов.
Р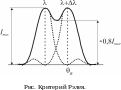 азрешающая
способность
азрешающая
способность
Разрешающей способностью спектрального прибора принято называть
отношение
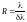 ,
,
где
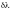 –
минимальный интервал между двумя
близкими спектральными
–
минимальный интервал между двумя
близкими спектральными
линиями, при котором они могут быть разрешены, то есть, отделены одна от
другой. В качестве критерия разрешения используется обычно критерий разрешения Рэлея. Спектральные линии с
близкими
значениями
и
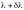 считаются
разрешенными, если главный максимум
дифракционной картины для
считаются
разрешенными, если главный максимум
дифракционной картины для
одной длины волны совпадает по своему положению с первым дифракционным минимумом в том же порядке для
другой длины волны (см. рис.).
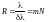
4.150 [5.141] Ознакомиться с решением.
Свет с длиной волны падает нормально на дифракционную решетку. Найти ее угловую дисперсию в зависимости от угла дифракции .
Решение:
Поскольку
мы имеем дело с дифракционной решеткой,
то запишем условие главных фраунгоферовых
максимумов : 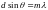 .
.
Как известно угловая дисперсия дифракционной решетки:
.
Выразив
отношение
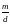 из первого уравнения и подставив его
во второе, получим, что
из первого уравнения и подставив его
во второе, получим, что
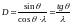
4.155 [5.146] Ознакомиться с решением.
Свет падает нормально на дифракционную решетку ширины l=6,5 см, имеющую 200 штрихов на миллиметр. Исследуемый спектр содержит спектральную линию с =670,8 нм, которая состоит из двух компонент, отличающихся на =0,015 нм. Найти:
а) в каком порядке спектра эти компоненты будут разрешены;
б) наименьшую разность длин волн, которую может разрешить эта решетка в области 670 нм.
Решение:
а)
Как известно, разрешающая способность
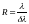 ,
также мы знаем, что для дифракционной
решетки
,
также мы знаем, что для дифракционной
решетки
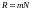 ,
где
,
где
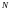 -кол-во
штрихов решетки,
-кол-во
штрихов решетки,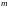 - порядок спектра.
- порядок спектра.
Определим
сколько штрихов у нашей решетки:
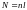 ,
где
,
где
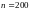 кол-во штрихов на миллиметр.
кол-во штрихов на миллиметр.
Тогда
окончательно для
получаем:
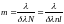 ■
■
б)
Мы знаем, что разрешающая способность
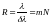 .
.
Для нахождения минимальной разности длин волн, которую может разрешить эта решетка, нам надо найти максимальный порядок спектра, что мы сделаем из условия максимума на решетке:
,
возьмем
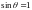
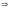
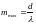
Тогда
для
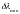 получаем, что
получаем, что 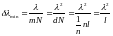 ■
■
(здесь
мы воспользовались тем, что период
решетки
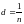 )
)
3. ДИФРАКЦИЯ ФРЕНЕЛЯ
ВЫВОД РАДИУСОВ И ПЛОЩАДЕЙ ЗОН ФРЕНЕЛЯ см. лекция, файл "Оптика в рисунках"
В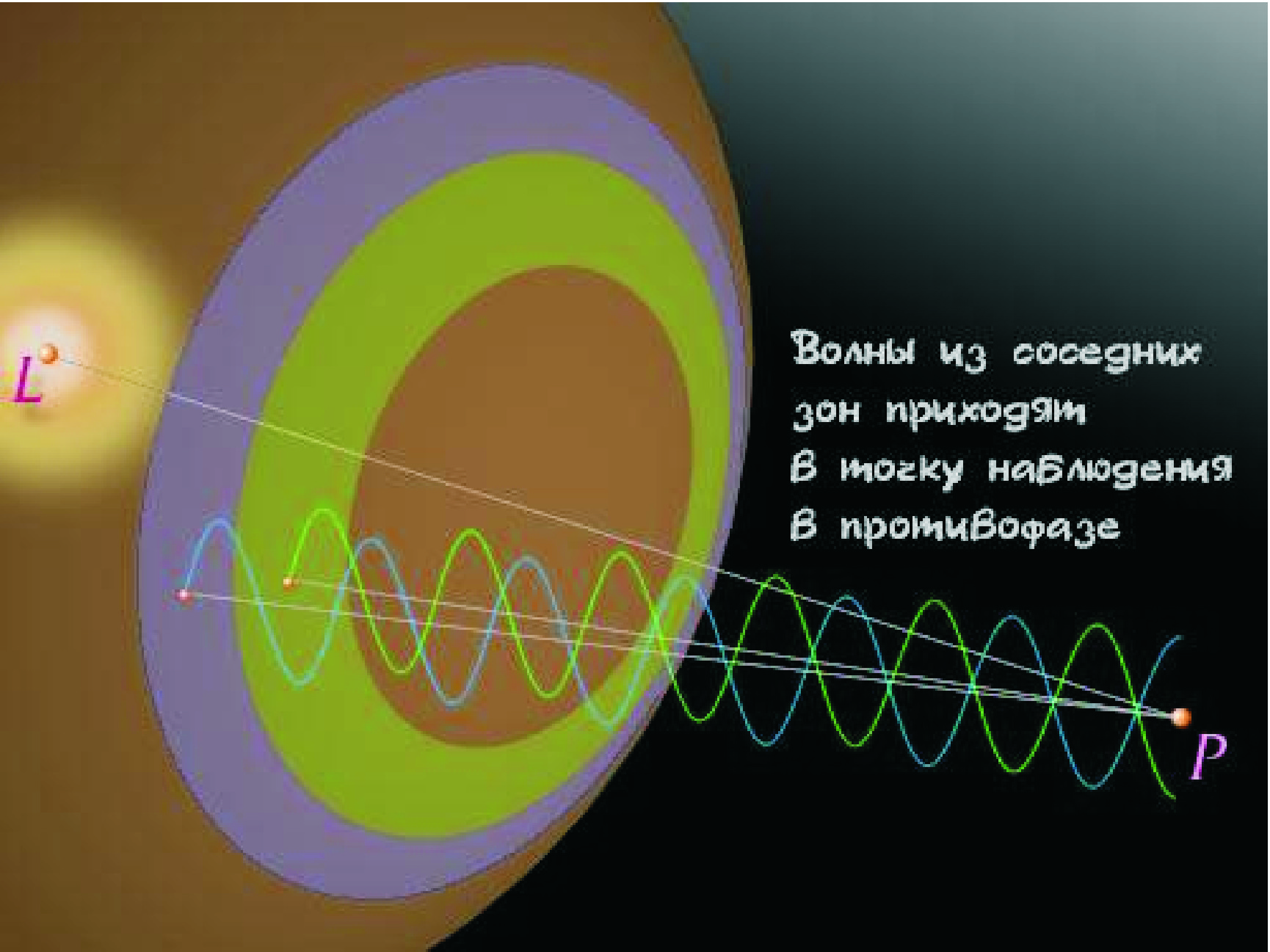 ычисление
результата интерференции вторичных
волн упрощается, если применить следующий
предложенный Френелем прием: разбиваем
волновую поверхность на кольцевые зоны
так, чтобы расстояния от краев соседних
зон до точки P
отличались на
ычисление
результата интерференции вторичных
волн упрощается, если применить следующий
предложенный Френелем прием: разбиваем
волновую поверхность на кольцевые зоны
так, чтобы расстояния от краев соседних
зон до точки P
отличались на
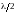 (см.рис.). Разность хода волн
соответствует разности фаз,
(см.рис.). Разность хода волн
соответствует разности фаз,
 равной
равной
 ,
т.е. волны от краев соседних зон приходят
в точку P
в противофазе и гасят друг друга при
интерференции.
,
т.е. волны от краев соседних зон приходят
в точку P
в противофазе и гасят друг друга при
интерференции.
Р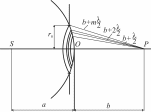 адиус
адиус
 -ой
зоны определяется выражением
-ой
зоны определяется выражением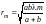
Площадь
m-зоны-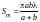 не
зависит от номера зоны.
(*)
не
зависит от номера зоны.
(*)
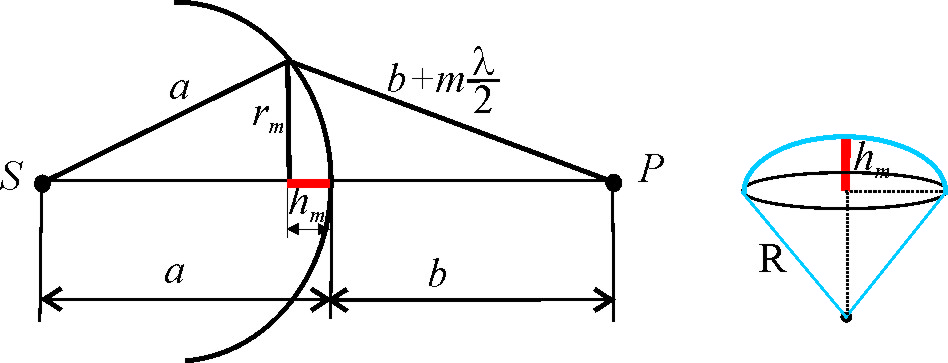
(*)Докажем
равенство площадей зон Френеля и найдем
их радиусы. Сначала вычислим площадь,
занимаемую первыми m
зонами Френели, т.е. площадь боковой
поверхности сферического сегмента,
которая определяется формулой
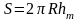 ,
где R
- радиус сферы и
,
где R
- радиус сферы и
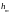 - высота сегмента, или в наших обозначениях
- высота сегмента, или в наших обозначениях
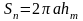 (рис.).
Высоту
сегмента
найдем, приравняв выражения для
(рис.).
Высоту
сегмента
найдем, приравняв выражения для
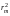 ,
полученные по теореме Пифагора из
прямоугольных треугольников:
,
полученные по теореме Пифагора из
прямоугольных треугольников: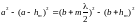 Пренебрегая
ввиду малости длины световой волны
величиной
Пренебрегая
ввиду малости длины световой волны
величиной
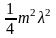 (тем самым считая, что число зон не
слишком велико), находим
(тем самым считая, что число зон не
слишком велико), находим
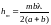 Площадь
m-ой
зоны получим как разность площадей m
и (m-1)
зон:
Площадь
m-ой
зоны получим как разность площадей m
и (m-1)
зон:
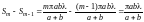
4.112 [5.103]
Между точечным источником света и экраном поместили диафрагму с круглым отверстием, радиус которого r можно менять. Расстояния от диафрагмы до источника и экрана равны а=100 см и b=125 см. Определить длину волны света, если максимум освещенности в центре дифракционной картины на экране наблюдается при r1=1,00 мм и следующий максимум при r2=1,29 мм.
Указание:
вывести формулу
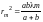 Далее,
очевидно,
что между двумя соседними максимумами
для точки наблюдения должны быть 2 зоны
Френеля.
Далее,
очевидно,
что между двумя соседними максимумами
для точки наблюдения должны быть 2 зоны
Френеля.
4.114 [5.105]
Плоская монохроматическая световая волна с интенсивностью I0 падает нормально на непрозрачный экран с круглым отверстием. Какова интенсивность света I за экраном в точке, для которой отверстие:
а) равно первой зоне Френеля; внутренней половине первой зоны;
б) сделали равным первой зоне Френеля и затем закрыли его
половину(по диаметру)?
4.115 [5.106]
Монохроматическая плоская световая волна с интенсивностью I0 падает нормально на непрозрачный диск, закрывающий для точки наблюдения Р первую зону Френеля. Какова стала интенсивность света I в точке Р после того как у диска удалили:
а) половину (по диаметру)?
б) половину внешней половины первой зоны Френеля (по диаметру)?
4.117 [5.108]
П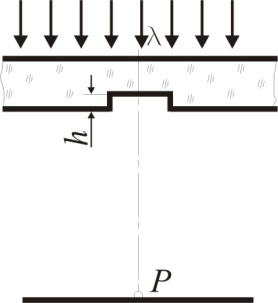 лоская
световая волна с
лоская
световая волна с
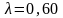 мкм падает нормально на достаточно
большую стеклянную пластину, на
противоположной стороне которой сделана
круглая выемка (рис.). Для точки наблюдения
мкм падает нормально на достаточно
большую стеклянную пластину, на
противоположной стороне которой сделана
круглая выемка (рис.). Для точки наблюдения
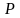 она представляет собой первые полторы
зоны Френеля. Найти глубину
она представляет собой первые полторы
зоны Френеля. Найти глубину
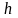 выемки, при которой интенсивность в
точке
будет:
выемки, при которой интенсивность в
точке
будет:
а) максимальной;
б) минимальной;
в) равной интенсивности падающего света.
4.119 [5.110]
Свет с длиной волны =0,60 мкм падает нормально на поверхность стеклянного диска, который перекрывает полторы зоны Френеля для точки наблюдения Р. При какой толщине этого диска интенсивность света в точке Р будет максимальной (минимальной)?
ТЕСТЫ
1 .Дифракция от круглого отверстия
Поставим
на пути плоской световой волны
интенсивности
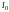 непрозрачный экран
с круглым отверстием радиуса
непрозрачный экран
с круглым отверстием радиуса
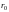 .
Точка наблюдения М находятся на оси
отверстия.
.
Точка наблюдения М находятся на оси
отверстия.
Когда отверстие открывает для точки наблюдения первую зону Френеля, то интенсивность I в точке М:
1.
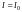 ;
2.
;
2.
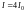 ;
3.
;
3.
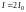 ;
4.
;
4.
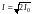 ;
5.
;
5.
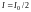
2.Дифракция от диска.
Поставим на пути плоской световой волны интенсивности непрозрачный диск. Точка наблюдения М находится на оси диска. Если диск закрывает для точки наблюдения М первую зону Френеля, то интенсивность I в данной точке:
1.
;
2.
;
3.
;
4.
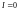 5.
;
5.
;