
- •Ознакомиться с решением задачи из лекции Гармонический осциллятор Колебания груза на пружине
- •2. Метод векторных диаграмм см. В лекции!!!
- •Метод векторных диаграмм. Сложение колебаний
- •Алгоритм сложения колебаний с помощью векторных диаграмм
- •Ознакомиться с решением задачи из лекции
- •3. Электрические колебания
- •Ознакомиться с решениями задач, приведенных ниже и с задачей, решенной на лекции "Вынужденные электрические колебания" методом векторных диаграмм.
- •4. Упругие волны
- •5. Электромагнитные волны
- •Тестовые задания
- •См. Калашников и Кожевников ( книга выслана), гл.4 , пп. 17-20, с решениями.
- •Тема 4 «Электрические колебания», в конце презентации тесты «Проверь себя» с решениями.
- •Еще несколько тестов без решений, но с ответами (объяснения - за вами). Тестовые вопросы
- •Ответы к тестам
МОДУЛЬ 1 КОЛЕБАНИЯ И ВОЛНЫ
ЗАДАЧИ И ТЕСТЫ НА ПЕРВУЮ КОНТРОЛЬНУЮ И ЭКЗАМЕН
Механические и электрические колебания
Л-4, №№ 3.2а (4.2а), 3.6 (4.5), 3.7 (4.7), 3.19 (4.18 ), 3.22 (4.21), 3.26 (4.24), 3.116 (4.108) ,
3.128 (4.120), 3.131 (4.123), 3.150 [4.142]
1. Механические колебания.
3.2а
[4.2а]
![]() .(Mожет
быть на экзамене в тестовой части).
.(Mожет
быть на экзамене в тестовой части).
Некоторая точка
движется вдоль оси х
по закону
![]() .
Найти амплитуду и период колебаний;
изобразить график
.(Mожет
быть на экзамене в тестовой части).
.
Найти амплитуду и период колебаний;
изобразить график
.(Mожет
быть на экзамене в тестовой части).
3.6 [4.5] (Mожет быть на экзамене в тестовой части).
Точка совершает
гармонические колебания вдоль некоторой
прямой с периодом
![]() и амплитудой
и амплитудой
![]() .Найти
среднюю скорость точки за время, в
течении которого она проходит путь
.Найти
среднюю скорость точки за время, в
течении которого она проходит путь
![]() :
:
a) из крайнего положения;
б) из положения равновесия.
3.7 [4.7]
Найти графически амплитуду А колебаний, которые возникают при сложении следующих колебаний:
а)
![]() ,
,
![]() ;
;
б)
![]() ,
,![]() ,
,![]()
3.19 [4.18 ]
Неподвижное тело,
подвешенное на пружинке, увеличивает
ее длину на
![]() .
Найти период малых вертикальных колебаний
тела.
.
Найти период малых вертикальных колебаний
тела.
3.22 [4.21]
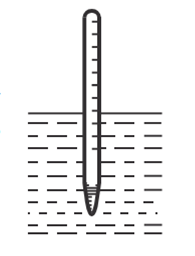
Вычислить период
малых колебаний ареометра (рис.), которому
сообщили небольшой толчок в вертикальном
направлении. Масса ареометра
![]() ,
радиус его трубки
,
радиус его трубки
![]() ,
плотность жидкости
,
плотность жидкости
![]() .
Сопротивление жидкости пренебрежимо
мало.
.
Сопротивление жидкости пренебрежимо
мало.
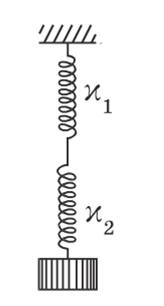
3.26 [4.24] (Может быть на экзамене в тестовой части).
Найти период малых
вертикальных колебаний тела массы
![]() в системе показанной на
в системе показанной на
(рис.) Жесткости
пружинок
![]() и
и
![]() .
.
Ознакомиться с решением задачи из лекции Гармонический осциллятор Колебания груза на пружине
П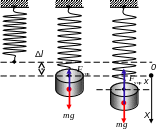 римером
гармонических колебаний может служить
поведение системы, состоящей из груза
массы m
и лёгкой пружины с жёсткостью k,
в поле сил тяжести. После того, как на
пружине закрепили груз, она стала длиннее
на Δl:
римером
гармонических колебаний может служить
поведение системы, состоящей из груза
массы m
и лёгкой пружины с жёсткостью k,
в поле сил тяжести. После того, как на
пружине закрепили груз, она стала длиннее
на Δl:
![]()
![]()
В результате сила тяжести будет скомпенсирована, и появится новое положение равновесия. Выведем систему из этого положения:
![]()
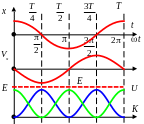
Направим ось X вниз, и выберем её начало в новом положении равновесия. Тогда:
![]()
![]()
![]()
![]()
![]()
![]()
Отклонение от положения равновесия:
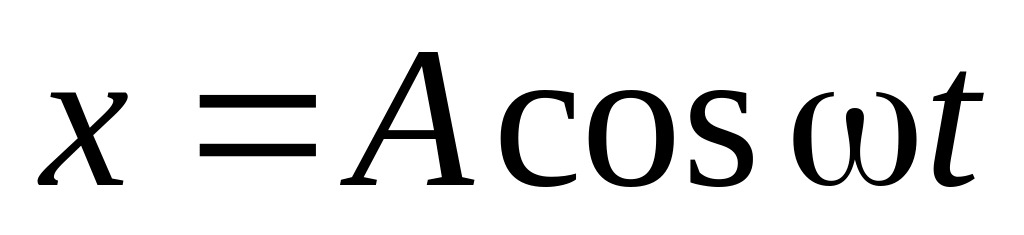
Скорость:
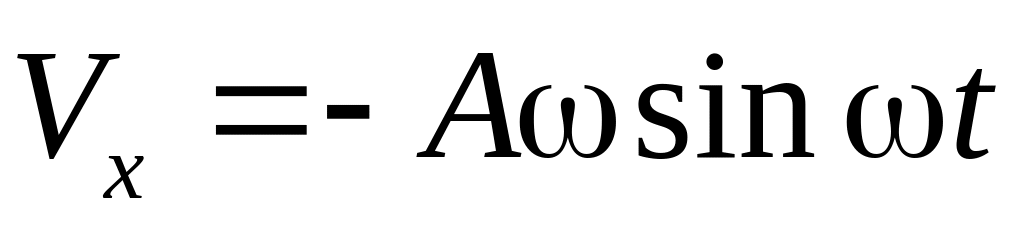
![]() – амплитуда
скорости.
– амплитуда
скорости.
Потенциальная энергия:
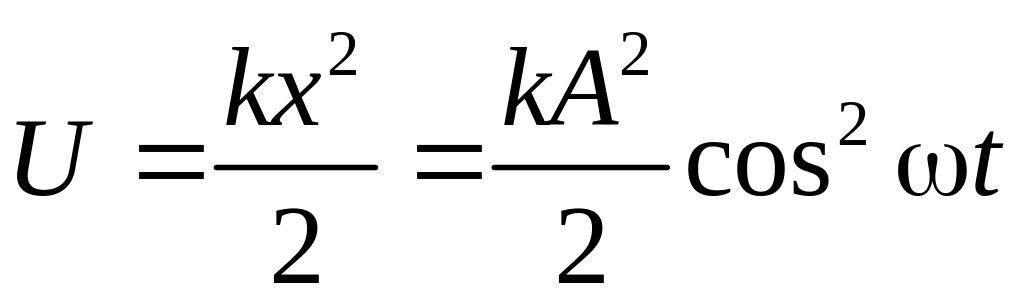
Кинетическая энергия:
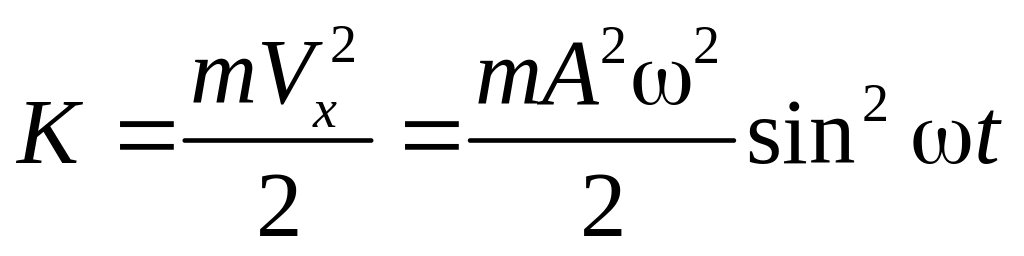
![]()
![]()
2. Метод векторных диаграмм см. В лекции!!!
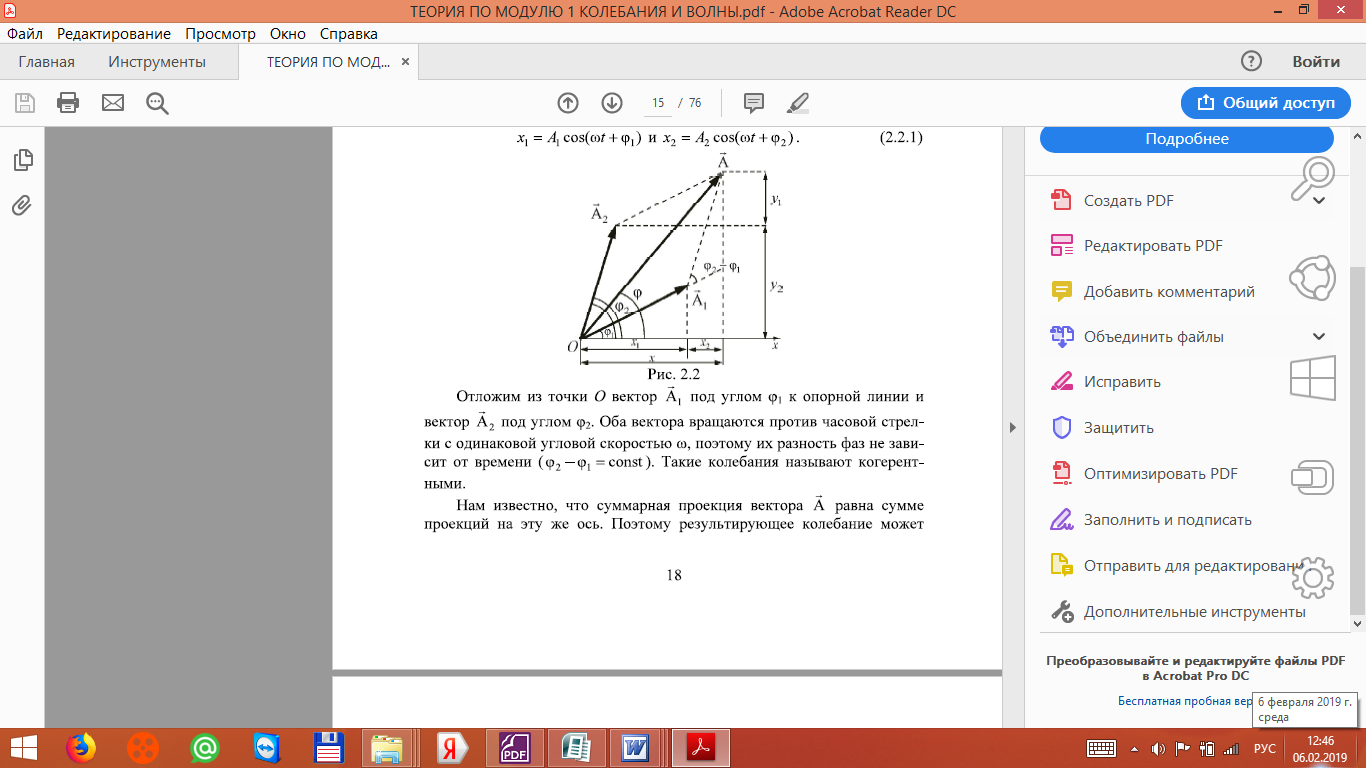
Метод векторных диаграмм. Сложение колебаний
П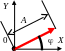 усть
закон движения имеет вид
усть
закон движения имеет вид
![]() .
.
Рассмотрим
вектор
![]() :
:
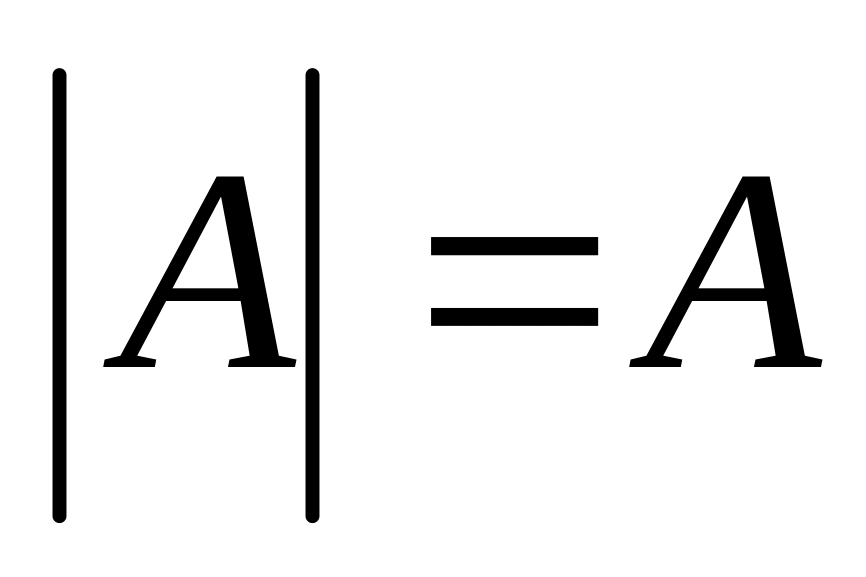
Угол между вектором и осью Ox равен φ.
Если теперь заставить этот вектор равномерно вращаться против часовой стрелки вокруг начала координат с угловой скоростью ω, то его проекция на ось Оx будет совершать гармоническое колебание по исходному закону . Во многих задачах оказывается удобным математические операции над величиной x заменить операциями над соответствующим вектором . Этим методом удобно складывать колебания одинаковой частоты.
Алгоритм сложения колебаний с помощью векторных диаграмм
Привести все колебания к виду
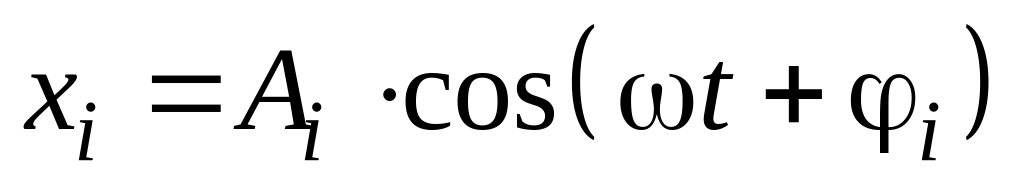 .
Использовать формулы:
.
Использовать формулы:
Формула приведения:
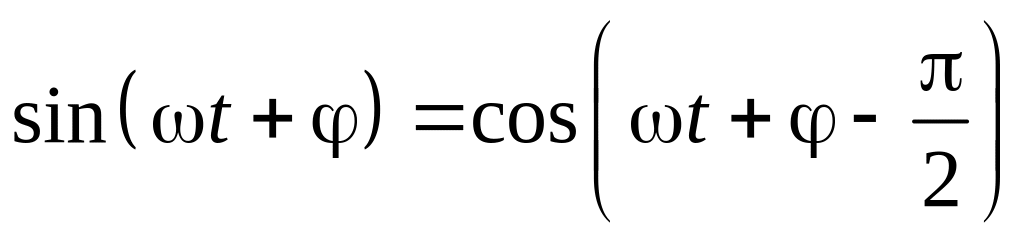 .
.Для смены знака надо поменять фазу на π:
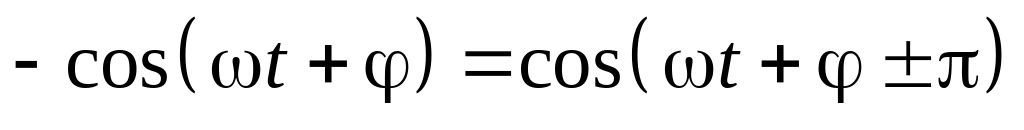 .
.
Для каждого колебания построить векторную диаграмму:
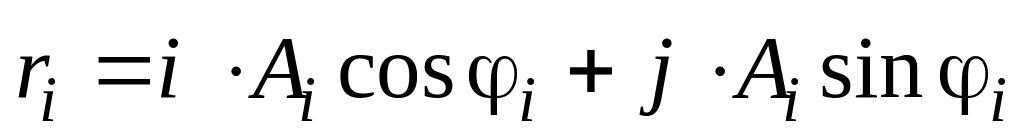 .
.Сложить полученные вектора по правилу сложения векторов:
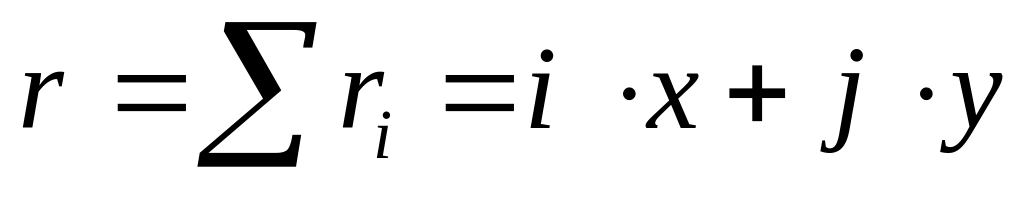 .
.По результирующему вектору
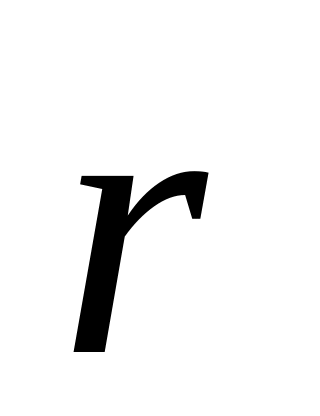 рассчитать амплитуду и фазу суммарного
колебания:
рассчитать амплитуду и фазу суммарного
колебания:
![]()
Пример: Для двух колебаний можно сразу воспользоваться готовыми формулами:
![]()
Ознакомиться с решением задачи из лекции
Установившиеся
колебания представляют собой гармонические
колебания. Подберем начало отсчета
времени таким образом, чтобы начальная
фаза была равна нулю, и будем искать
решение – функцию вида
![]() .
Уравнение вынужденных колебаний
.
Уравнение вынужденных колебаний
![]() .
Построим векторную диаграмму,
соответствующую этому уравнению. В
левой части 3 слагаемых:
.
Построим векторную диаграмму,
соответствующую этому уравнению. В
левой части 3 слагаемых:
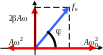 ,
поэтому слагаемому
,
поэтому слагаемому
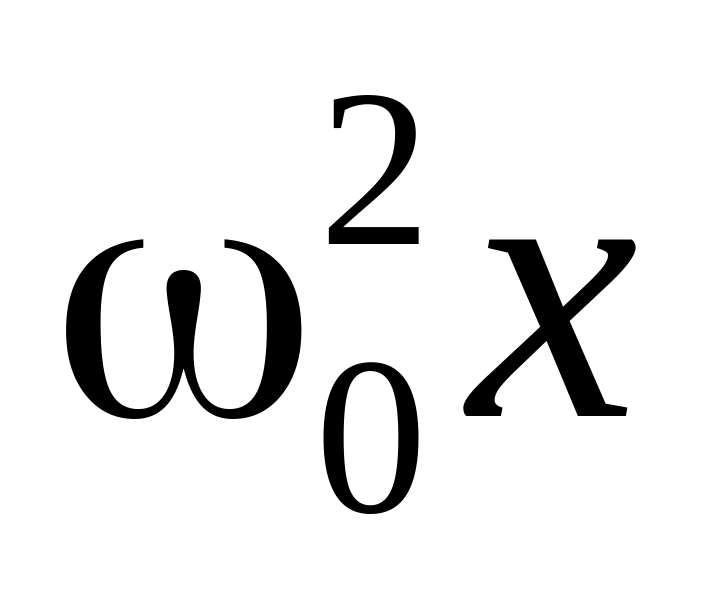 соответствует вектор длины
соответствует вектор длины
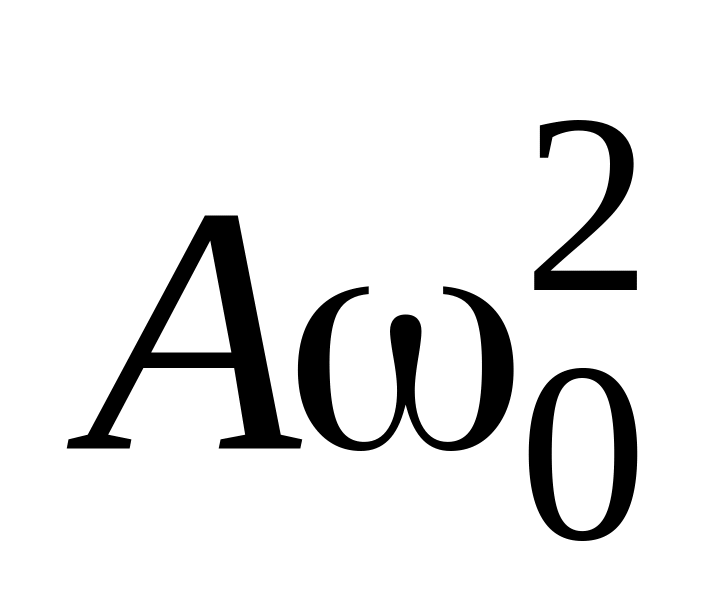 ,
направленный вдоль оси абсцисс;
,
направленный вдоль оси абсцисс;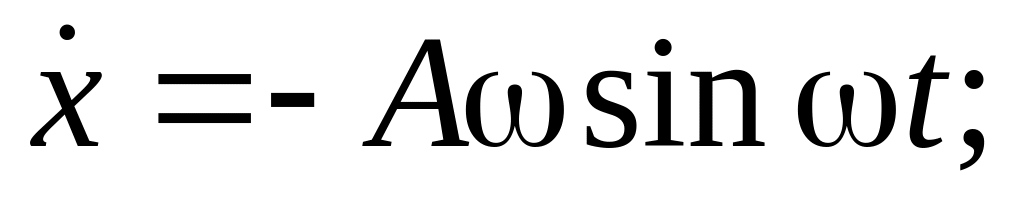 поэтому слагаемому
поэтому слагаемому
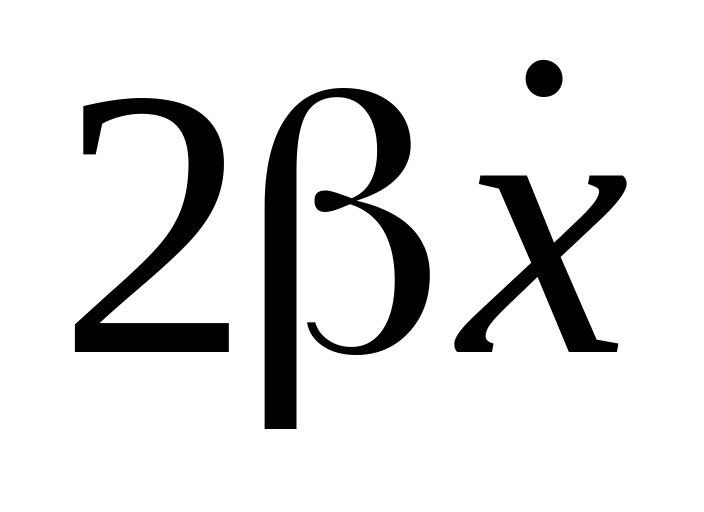 соответствует вектор длины
соответствует вектор длины
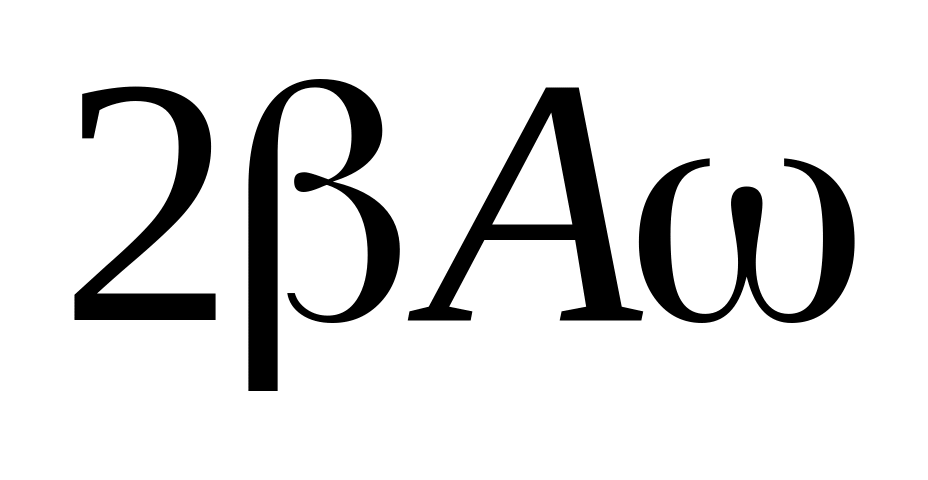 ,
составляющий угол π/2 с положительным
направлением оси абсцисс;
,
составляющий угол π/2 с положительным
направлением оси абсцисс;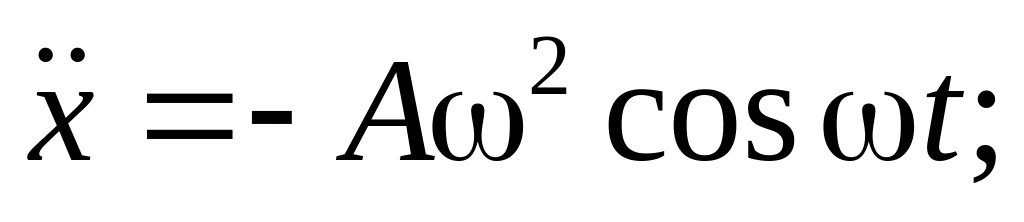 поэтому слагаемому
поэтому слагаемому
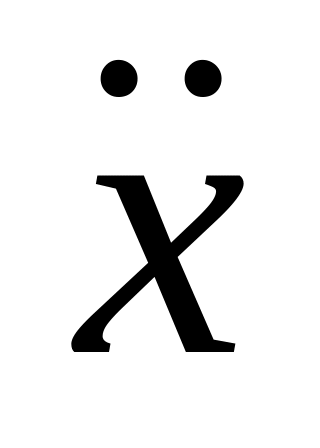 соответствует вектор длины
соответствует вектор длины
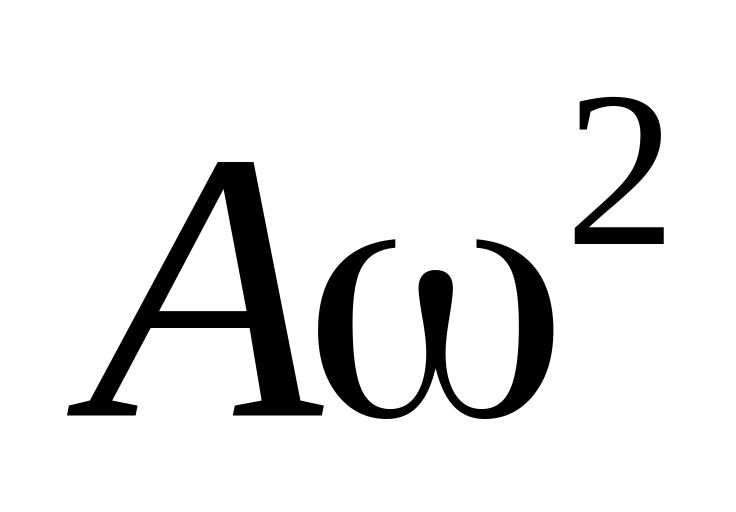 ,
составляющий угол π с положительным
направлением оси абсцисс;
,
составляющий угол π с положительным
направлением оси абсцисс;
Построим эти вектора и сложим их по правилу сложения векторов. Результирующий вектор и будет равен правой части уравнения вынужденных колебаний. Из рисунка видно, что амплитуда и фаза этого колебания равны:
![]()
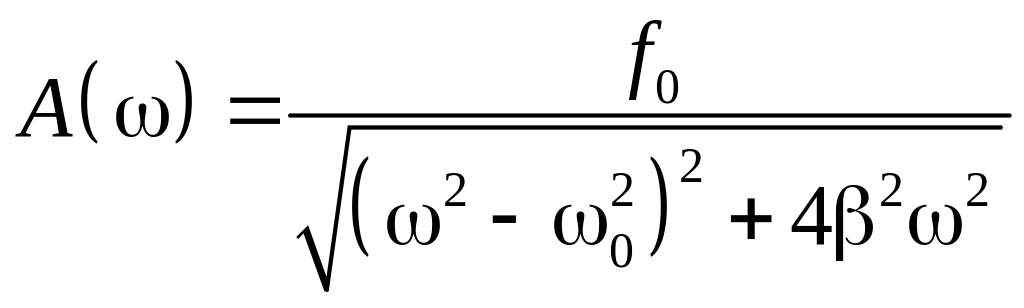
![]()
3. Электрические колебания
3.116 [4.108]
В контуре,
состоящем из
конденсатора емкости
![]() и катушки с индуктивностью
и катушки с индуктивностью
![]() ,
совершаются свободные незатухающие
колебания, при которых амплитуда
напряжения на конденсаторе равна
,
совершаются свободные незатухающие
колебания, при которых амплитуда
напряжения на конденсаторе равна
![]() .
Найти связь между током
.
Найти связь между током
![]() в
контуре и напряжением
в
контуре и напряжением
![]() на конденсаторе.
на конденсаторе.
3.128 [4.120]
Колебательный контур
состоит из конденсатора емкости
![]() и катушки с индуктивностью
и катушки с индуктивностью
![]() и активным сопротивлением
и активным сопротивлением
![]() .
Найти отношение энергии магнитного
поля катушки к энергии электрического
поля конденсатора в момент максимума
тока.
.
Найти отношение энергии магнитного
поля катушки к энергии электрического
поля конденсатора в момент максимума
тока.
3.131 [4.123]
Колебательный контур
имеет емкость
![]() ,
индуктивность
,
индуктивность
![]() и активное сопротивление
и активное сопротивление
![]() .Через
сколько колебаний амплитуда в этом
контуре уменьшится в е раз?
.Через
сколько колебаний амплитуда в этом
контуре уменьшится в е раз?
3.150 [4.142]
Цепь, состоящая из последовательно соединенных конденсатора емкости C=22мкФ и катушки с активным сопротивлением R=20 Ом и индуктивностью L=0,35 Гн, подключена к сети переменного напряжения с амплитудой Um=180В и частотой ω=314 с-1
Найти:
а) амплитуду тока в цепи;
б) разность фаз между током и внешним напряжением;
