
Физика второй семестр / Экзамен / Zadachi_na_ekzamen / !!!Семинар 6 Многоэлектронные атомы
.docСеминар 16
№ 6.113.
Найти возможные
значения полных механических моментов
атомов, находящихся в состояниях
![]() и
и
![]() .
.
Решение:
Полный механический момент атома находится по формуле:
![]() ,
,
где
![]() может принимать значения от
может принимать значения от
![]() до
до
![]() .
В первом случае (для атома, находящегося
в состоянии
.
В первом случае (для атома, находящегося
в состоянии
![]() ),
из общего обозначения
),
из общего обозначения
![]() находим:
находим:
![]() .
.
Тогда
![]() может принимать значения:
может принимать значения:
![]() ,
,
тогда полный механический момент может быть равен:
![]() .
.
Аналогично для атома, находящегося в
состоянии
![]() ,
получаем:
,
получаем:
![]() .
.
может принимать значения:
![]() ,
,
тогда полный механический момент может быть равен:
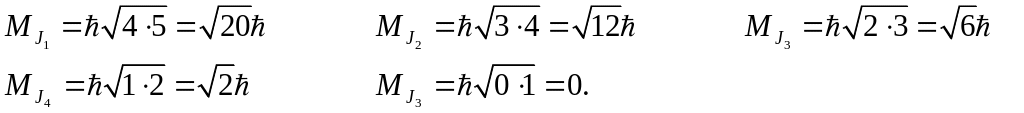
№ 6.116.
Атом находится в
состоянии, мультиплетность которого
равна трем, а полный механический момент
![]() .
Каким может быть соответствующее
квантовое число
.
Каким может быть соответствующее
квантовое число
![]() ?
?
Решение:
Полный механический момент атома находится по формуле:
![]()
![]()
![]() .
.
По определению, мультиплетность атома
![]() ,
тогда
,
тогда
![]()
![]() .
.
Вспомним, что представляет из себя спектр значений :
![]() .
.
Из первого значения
![]() ,
получаем:
,
получаем:
![]()
![]() .
.
Рассмотрим последнее значение
![]() :
:
![]()
![]() ,
,
но т.к.
![]() может принимать только положительные
значения,
может принимать только положительные
значения,
![]() .
Очевидно,
может принимать и все промежуточные
значения между полученными нами крайними
значениями:
.
Очевидно,
может принимать и все промежуточные
значения между полученными нами крайними
значениями:
![]() .
.
№ 6.117.
Определить максимально возможный орбитальный механический момент атома в состоянии, мультиплетность которого равна пяти и кратность вырождения по - семи. Написать спектральное обозначение соответствующего терма.
Решение:
По определению, кратность вырождения по равна:
![]()
![]() .
.
По определению мультиплетности,
![]()
![]() .
.
Теперь легко найти максимальное значение из условия:
![]()
![]() .
.
Тогда максимально возможный орбитальный механический момент равен:
![]() .
.
Спектрально обозначение соответствующего терма будет выглядеть следующим образом:
![]()
№ 6.122.
Установить, какие из нижеперечисленных переходов запрещены правилами отбора:
Решение:
Вспомним правила отбора:
![]()
![]()
![]() .
.
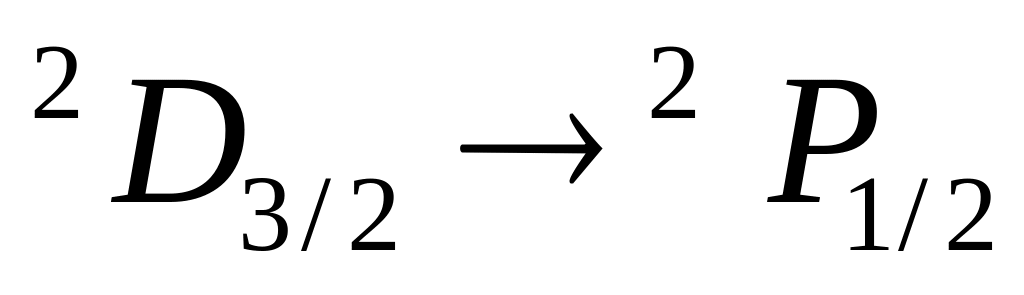 -
возможен:
,
-
возможен:
,
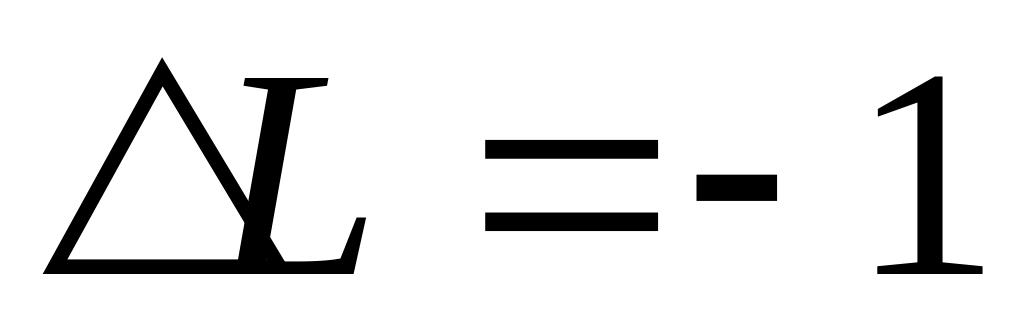 ,
,
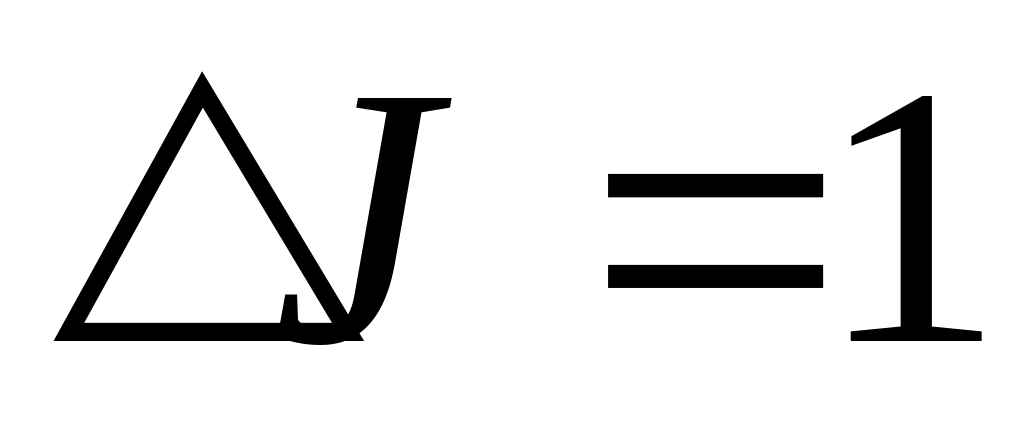 ;
;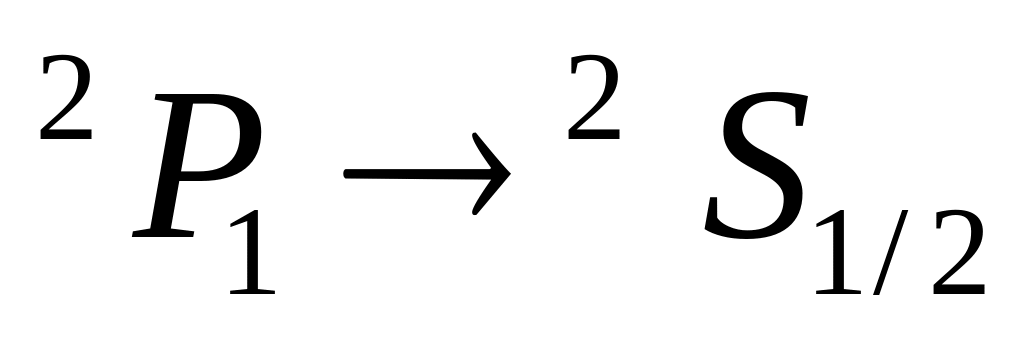 -
невозможен:
-
невозможен:
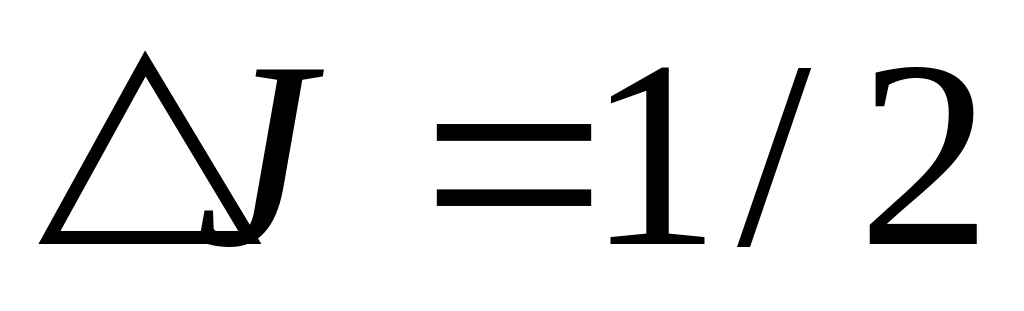 ;
;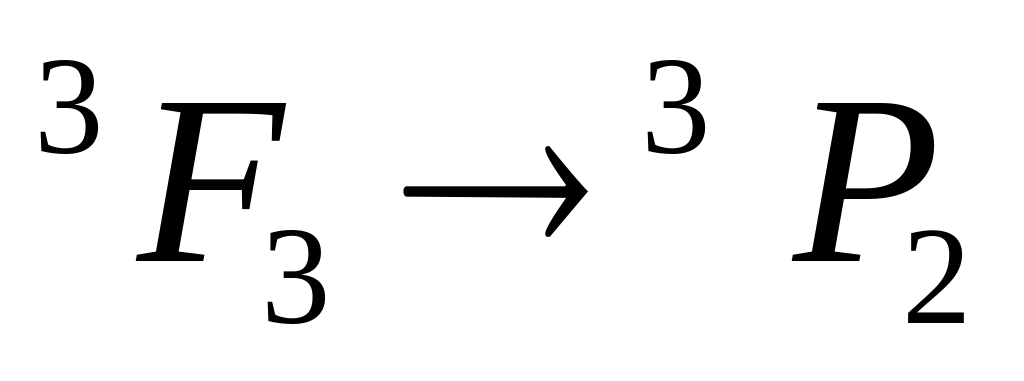 -
невозможен:
-
невозможен:
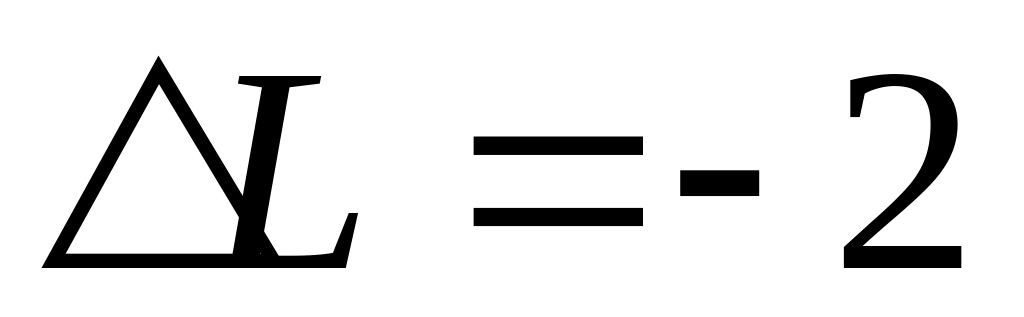 ;
;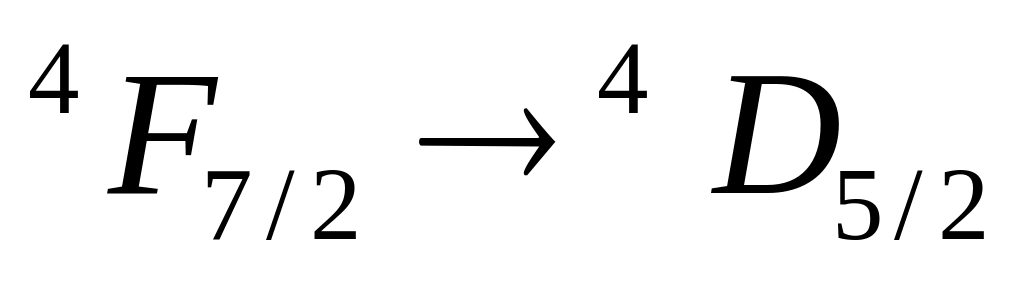 -
возможен:
,
,
-
возможен:
,
,
№ 6.123.
Определить суммарную
кратность вырождения
![]() -
состояния атома лития. Каков физический
смысл этой величины?
-
состояния атома лития. Каков физический
смысл этой величины?
Решение:
В задаче зафиксированы n
и l квантовые числа.
Значит, данное состояние будет вырождено
по
![]() и
и
![]() .
Иными словами, суммарная кратность
вырождения в нашем случае равна:
.
Иными словами, суммарная кратность
вырождения в нашем случае равна:
![]() ,
,
поскольку если указан спин, то его
проекция может принимать
![]() значений; если указан
,
то его проекция может принимать
значений; если указан
,
то его проекция может принимать
![]() значений. В нашей задаче
значений. В нашей задаче
![]() (поскольку атом лития имеет один
электрон),
(поскольку атом лития имеет один
электрон),
![]() .
Итак, имеем:
.
Итак, имеем:
![]()
![]() .
.
Тогда суммарная кратность вырождения равна:
![]()
№ 6.160.
Некоторый атом
находится в состоянии, для которого
![]() ,
полный механический момент
,
полный механический момент
![]() ,
а магнитный момент равен нулю. Написать
спектральный символ соответствующего
терма.
,
а магнитный момент равен нулю. Написать
спектральный символ соответствующего
терма.
Решение:
По условию, магнитный момент
![]() :
:
![]() .
.
Поскольку для полного механического момента имеем:
![]()
![]() ,
,
значит
![]() .
Приравняв фактор Ланде к нулю, получим:
.
Приравняв фактор Ланде к нулю, получим:
![]() .
.
Спектральный символ соответствующего
терма, для которого
,
,
![]() ,
имеет вид:
,
имеет вид:
![]()
№ 6.165.
На сколько подуровней расщепится в слабом магнитном поле терм:
Решение:
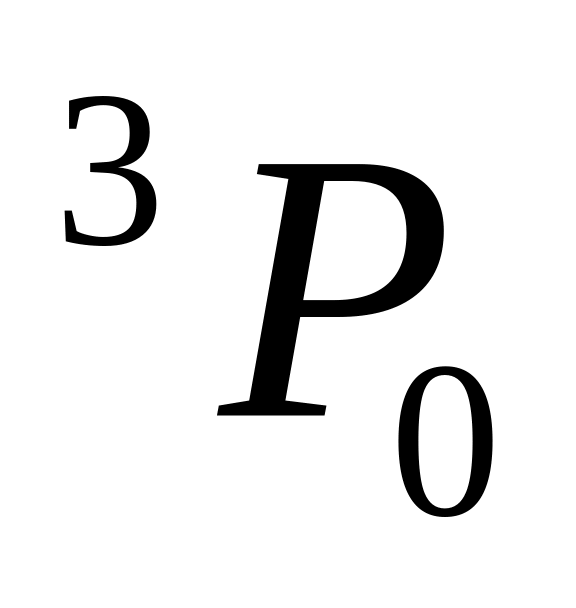 ;
;
В общем случае, терм
![]() расщепляется на состояния с различными
,
всего
расщепляется на состояния с различными
,
всего
![]() состояний, за исключением случаев, когда
фактор Ланде = 0. Энергия взаимодействия
атома с внешним полем описывается
уравнением:
состояний, за исключением случаев, когда
фактор Ланде = 0. Энергия взаимодействия
атома с внешним полем описывается
уравнением:
![]() ,
, ![]() ,
где
,
где
![]() .
.
Итак, терм
не расщепляется, поскольку
![]() .
.
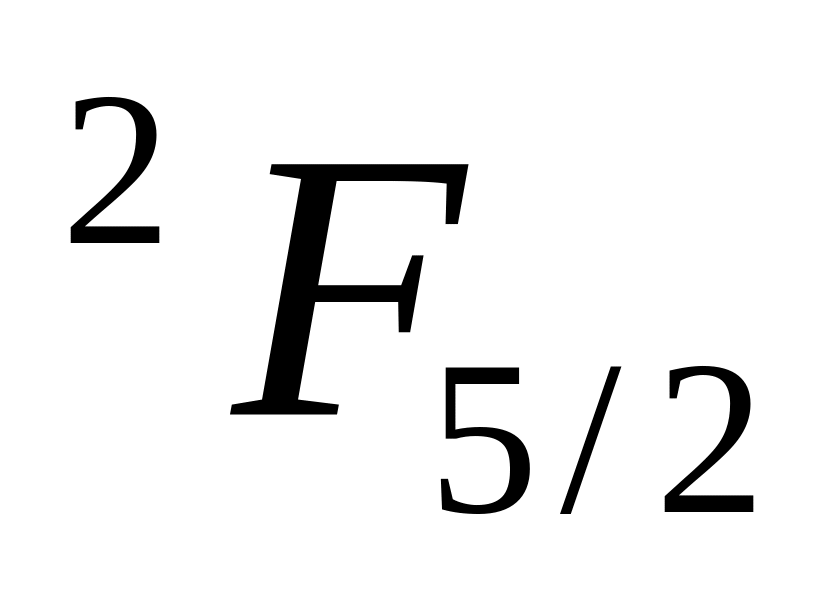 ;
;
Т.к. в случае, когда фактор Ланде равен нулю, терм не расщепляется, найдем фактор Ланде:
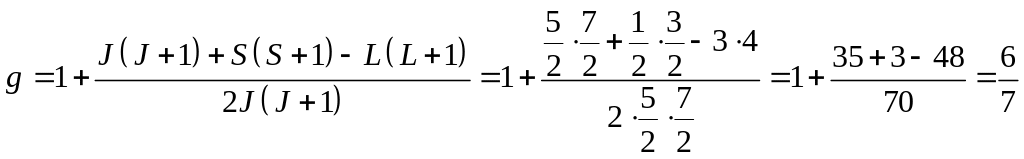 ,
,
значит терм расщепляется на
![]() подуровней.
подуровней.
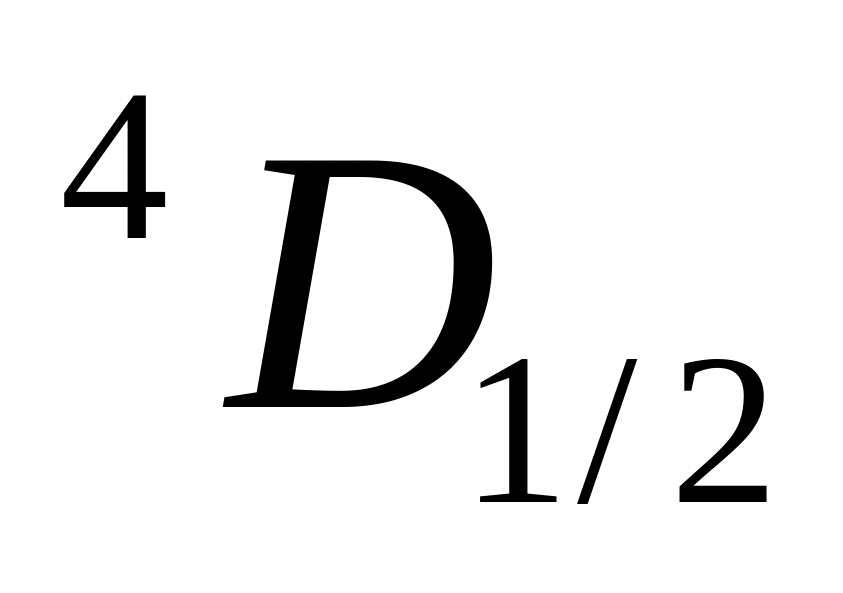 ;
;
Т.к. в случае, когда фактор Ланде равен нулю, терм не расщепляется, найдем фактор Ланде:
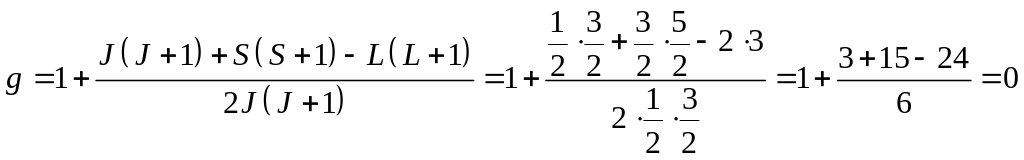 ,
,
значит терм не расщепляется.
