Физика второй семестр / Экзамен / Zadachi_na_ekzamen / !!!Семинар 5 УравнениеШредингера (СРС)

Семинар 15 (СРС ПО ЛЕКЦИИ)

№6.80

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Найти ширину ямы, если разность энергии между уровнями с и составляет .

Решение:

Чтобы вычислить длину ямы, получим сначала выражение для энергии электрона в зависимости от уровня, на котором он находится. Рассмотрим уравнение Шредингера внутри ямы:

.

По условию, внутри ямы , тогда примем и с учетом одномерности запишем:

.

Для решения этого дифференциального уравнения, проведем аналогию с уравнениями вида , для которых решение следует искать в виде , тогда

.

Рассмотрим две граничные точки, в которых волновая функция ввиду ее непрерывности должна быть равна нулю:

: ;

: .

Вспоминаем, что в наших обозначениях , тогда

.

. 

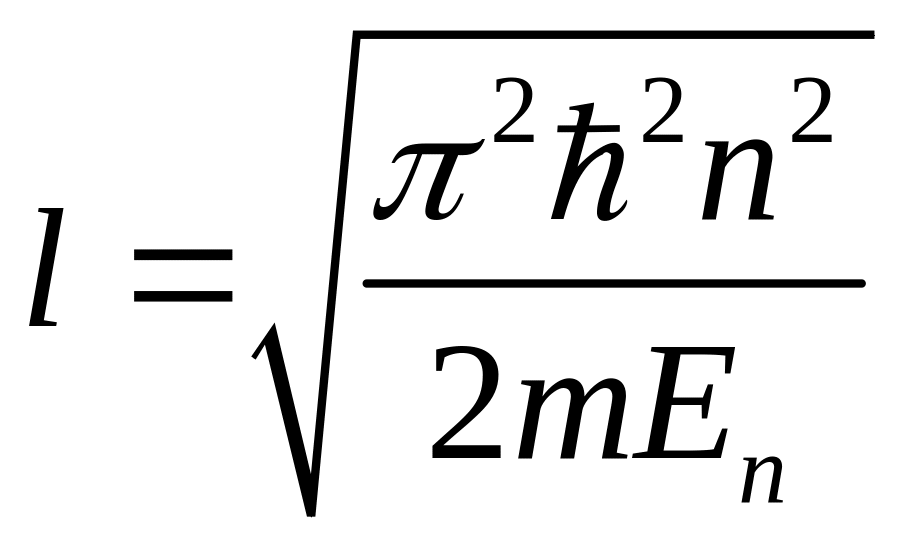№6.81 Частица находится в основном состоянии в одномерной прямоугольной потенциальной яме ширины l с абсолютно непроницаемыми стенками ( ). Найти вероятность пребывания частицы в области .

Решение: Согласно физическому смыслу -функции, вероятность нахождения частицы в элементарном объеме описывается выражением:

.

Наша задача – получить решение уравнение Шредингера для частицы, находящейся в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Запишем уравнение Шредингера:

.

С учетом того, что в яме потенциальная энергия частицы = 0, запишем:

.

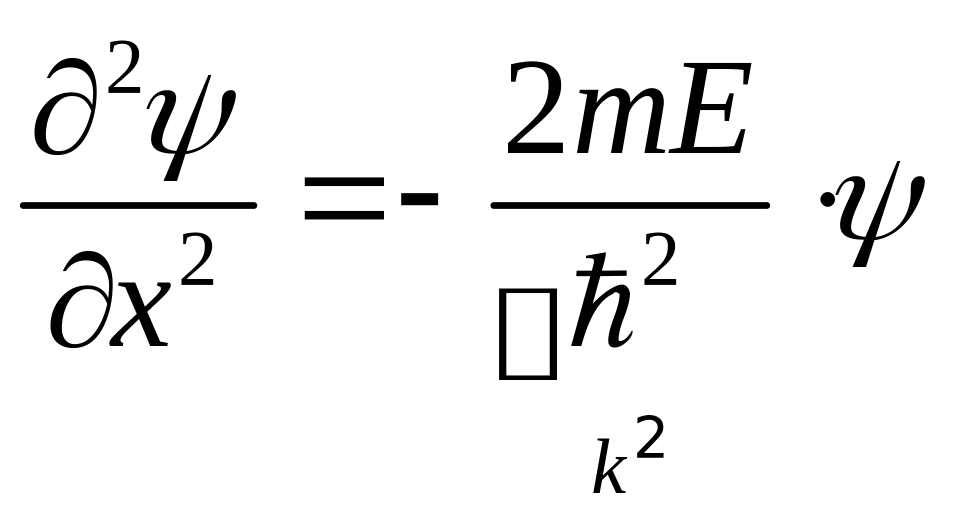
Решение последнего дифференциального уравнения нужно искать в виде:

.

Рассмотрим два граничных условия:

1) т.к. при ;

2) т.к. при , имеем:

,

причем , т.к. получится, что частицы нет ни внутри ямы, ни за ее пределами. Значит, волновая функция имеет вид:

.

Найдем константу . Из условий нормировки получим:

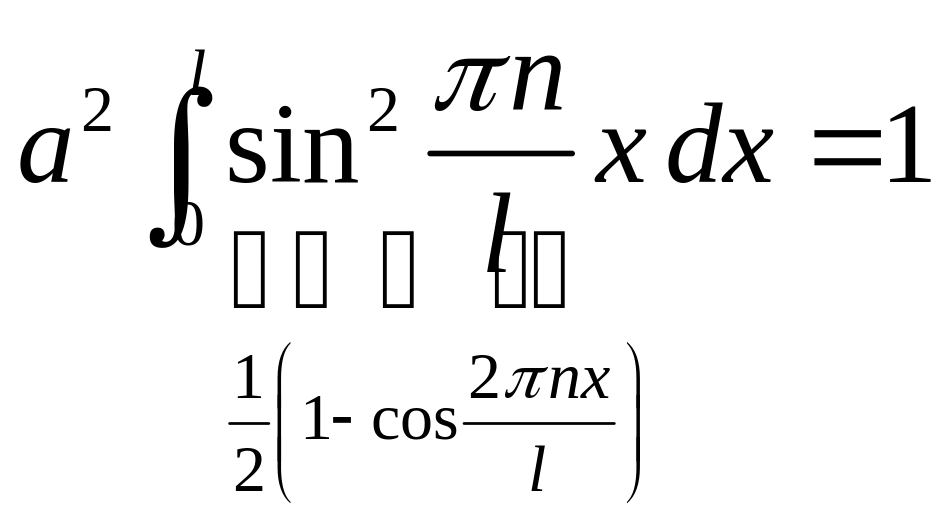
Таким образом, собственные функции имеют вид:

.

Теперь чтобы найти вероятность нахождения частицы в заданной области, нужно просто взять определенный интеграл:

. 
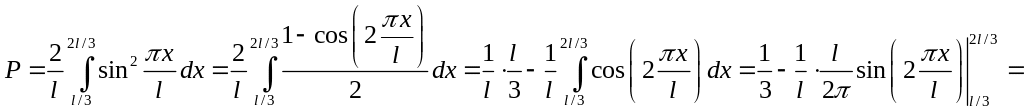