Физика второй семестр / Экзамен / Zadachi_na_ekzamen / !!!Семинар 4 Волна де Бройля Соотн. неопр

Семинар 3

№ 6.50

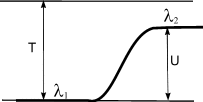
Частица движется слева направо в одномерном потенциальном поле, показанном на рисунке. Левее барьера, высота которого , кинетическая энергия частицы . Во сколько раз и как изменится дебройлевская длина волны при переходе через барьер? Решение:

Так как , барьер является низким, и можно найти дебройлевские длины волн и до и после барьера соответственно. Полная же энергия частицы до барьера равна ее кинетической энергии. Тогда получаем:

и , где и , тогда 



№6.59

Параллельный поток моноэнергетических электронов падает нормально на диафрагму с узкой прямоугольной щелью ширины . Определить скорость этих электронов, если на экране, отстоящем от щели на расстояние , ширина центрального дифракционного максимума .

Решение: Условие минимума для дифракции Фраунгофера на щели: , нас интересует . Тогда . Т.к. угол можно считать малым, то и (т.к. ширина главного максимума равна удвоенному расстоянию от центра до первого минимума). С другой стороны:

. Следовательно, . 

№6.60

Параллельный пучок электронов, ускоренных разностью потенциалов , падает нормально на диафрагму с двумя узкими щелями, расстояние между которыми . Определить расстояние между соседними максимума дифракционной картины на экране, расположенном на расстоянии от щелей.

Решение: Так как электроны ускоряются разностью потенциалов, то => Из условия максимума на решетке: , где нас интересует . Из-за малости углов можно считать: и . Вспоминаем результат, полученный при изучении схемы Юнга:

Тогда учитывая, что , получим: 

№6.72

Электрон с кинетической энергией локализован в области размером . Оценить с помощью соотношения неопределенностей относительную неопределенность его скорости.

Решение: Из соотношения неопределенностей получаем:

Поскольку и , получаем:



№6.73

Электрон находится в одномерной прямоугольной потенциальной яме с бесконечно высокими стенками. Ширина ямы . Оценить с помощью соотношения неопределенностей силу давления электрона на стенки ямы при минимально возможной энергии.

Решение: Давление на стенки ямы образуется из-за столкновения электронов со стенками. Тогда для нахождения силы давления мы можем воспользоваться законом сохранения импульса для электрона. Рассмотрим абсолютно упругий удар электрона о стенку (яма одномерная, поэтому записываем сразу в проекции на направление х):

.

При ударе импульс по модулю остается прежним, но меняет направление на противоположное, тогда . Для нахождения , воспользуемся соотношением неопределенностей. Полная энергия электрона в яме описывается выражением:

,

где в яме . Т.к. в условии сказано, что электрон обладает минимально возможной энергией, формальным минимумом выражения является . Тогда из закона сохранения импульса следует:

Из соотношениям неопределенностей имеем:

.

Т еперь оценим время между двумя столкновениями. Если электрон движется со скоростью , то между двумя ближайшими столкновениями об один фиксированный участок стенки пройдет время (см. рисунок):

,

где мы воспользовались нерелятивистской формулой для импульса: . Из механики известно, что , тогда



№6.75

Частица массой движется в одномерном потенциальном поле (гармонический осциллятор). Оценить с помощью соотношения неопределенностей минимально возможную энергию частицы в таком поле.

Решение: Полная энергия электрона в одномерном потенциальном поле описывается выражением:

.

Формальному минимуму этого выражения, очевидно, будут соответствовать следующие значения импульса и координаты:

, .

Тогда из соотношений:

.

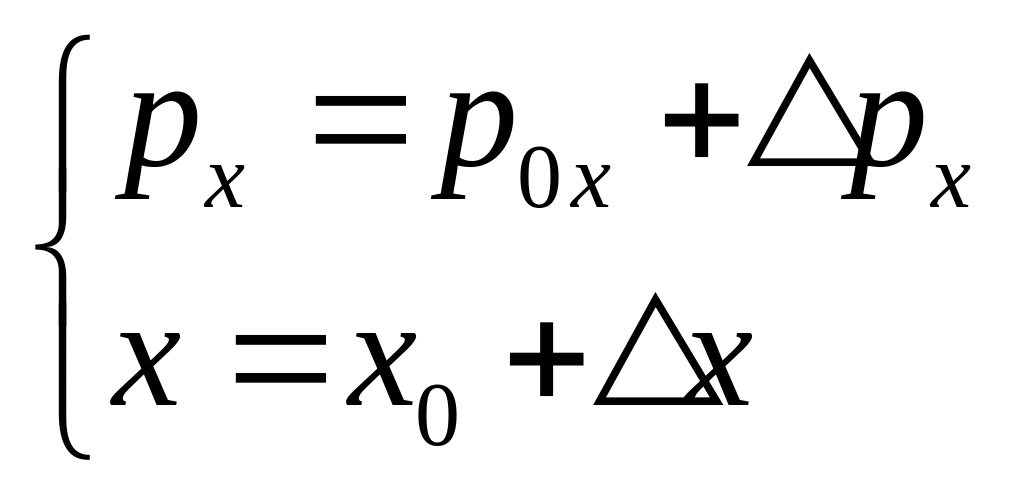
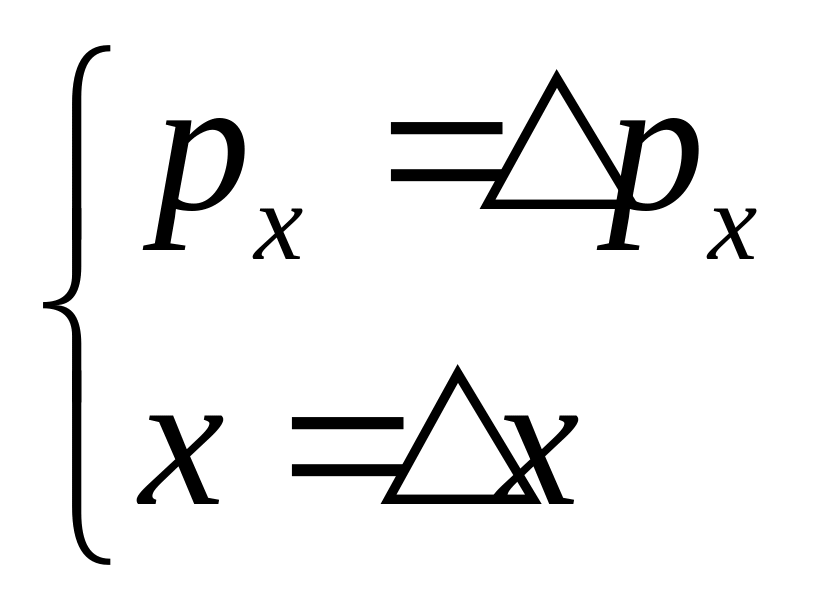Из соотношения неопределенностей, .

Тогда выражение для энергии приобретает следующий вид:

.

Продифференцируем для отыскания минимума функции:

Тогда подставив это значение в выражение для энергии, получим:

. 

№6.76

Оценить с помощью соотношения неопределенностей минимально возможную энергию электрона в атоме водорода и соответствующее эффективное расстояние его от ядра.

Решение: Для энергии электрона, движущегося в потенциальном поле ядра атома, имеем:

,

Из соотношения неопределенностей, для получения значения минимальной энергии (см. предыдущую задачу) , тогда:

.

Продифференцируем для нахождения минимума:

.

Подставив в функцию для энергии, получим:

. 