Лабораторная работа №18

Эффект Комптона

Лабораторная работа №18

Эффект Комптона

Цель работы: Исследование эффекта Комптона.

Теоретическая часть

Корпускулярно-волновым дуализмом называется универсальное свойство физических объектов проявлять себя в одних явлениях подобно волне, а в других - подобно частицам. Исторически корпускулярно-волновой дуализм был впервые обнаружен при изучении свойств света. С одной стороны, многочисленные эксперименты по наблюдению явлений дифракции и интерференции света однозначно свидетельствуют в пользу его волновой природы. С другой стороны, закономерности фотоэффекта и излучения абсолютно черного тела удалось теоретически объяснить лишь предположив, что свет представляет собой поток квантов энергии - фотонов.

Фотоном называется квант электромагнитного излучения, энергия которого определяется его частотой:

, (1)

где ħ = 1,0546·10^‑34 Джс - постоянная Планка.

В релятивистской динамике энергия и импульс движущейся частицы связаны соотношением:

(2)

где p - импульс частицы, m - её масса, а E - полная энергия, определяемая выражением:

(3)

Фотоны распространяются в вакууме со скоростью света c, поэтому для фотона знаменатель выражения (3) обращается в ноль. Следовательно, конечной энергией фотон может обладать, только если его масса m=0. С учетом этого факта из формулы (2) получим выражение для импульса фотона:

(4)

Таким образом, циклическая частота ω и длина волны λ характеризуют волновые свойства фотона, а энергия ε и импульс p - корпускулярные. Связь между ними выражается формулами (1) и (4).

Одним из наиболее убедительных экспериментальных доказательств корпускулярных свойств света является эффект Комптона.

Эффектом Комптона называется рассеяние жесткого рентгеновского излучения на образцах, состоящих из лёгких атомов, в результате чего в спектре рассеянного излучения наряду с исходной длиной волны возникает смещённая линия с длиной волны (комптоновское смещение). Все попытки объяснить закономерности этого явления с позиций волновой теории оказались несостоятельными. Успешную теорию эффекта Комптона удалось построить только в рамках квантовой теории: изменение длины волны рентгеновского кванта является результатом его упругого соударения с электроном.

а) б)

Рис. 1 – Схематическое изображение комптоновского рассеяния (а) и соответствующая векторная диаграмма закона сохранения импульса (б).

В атомах легких элементов энергия связи электрона с атомом мала по сравнению с энергией, передаваемой электрону рентгеновским квантом при рассеянии. Поэтому энергией связи электрона внутри атома можно пренебречь и считать все электроны свободными. Рассмотрим столкновение фотона со свободным электроном с позиции законов сохранения импульса и энергии. Введём следующие обозначения:

- энергия фотона до столкновения;

- энергия фотона после столкновения;

m_e - масса электрона;

m_ec² - энергия покоящегося свободного электрона (см. (3));

- энергия электрона после столкновения;

- импульс фотона до столкновения;

- импульс фотона после столкновения;

- импульс электрона после столкновения;

В этих обозначениях выражение закона сохранения энергии принимает вид:

(5)

Закон сохранения импульса:

(6)

На рис.1 (б) показана векторная диаграмма, соответствующая этому выражению. Применив к данному треугольнику теорему косинусов, с учетом связи энергии фотона с его импульсом (4) получим:

(7)

После столкновения электрон может стать релятивистским, поэтому уравнение связи его импульса и энергии имеет вид:

(8)

Выражая из формулы (5), а - из (7), после подстановки и несложных преобразований получим:

. (9)

Согласно (1) энергия фотона связана с его длиной волны формулой:

(10)

Подставив в (9) получим окончательную формулу:

(11)

где λ_C - комптоновская длина волны электрона - одна из важнейших атомных констант:

(12)

Соотношение (11) очень хорошо согласуется с наблюдаемой на опыте зависимостью комптоновского смещения от угла рассеяния θ. Схема соответствующей экспериментальной установки для измерения спектра рассеянного излучения показана на рис.2. Для определения длины волны рассеянного излучения в ней используется явление дифракции на кристалле. При попадании рентгеновских лучей на атомы твердого тела происходит их рассеивание электронами атомов. Наличие периодической структуры в твердом теле определяет интерференцию отдельных рассеянных волн. Направления дифракционных максимумов подчиняются уравнению Брэгга-Вульфа:

, (13)

где d – известное расстояние между кристаллографическими плоскостями; φ – угол скольжения (угол Брэгга); λ – длина волны; n - порядок дифракции.

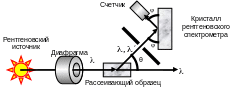
Рис. 2 – Схема классического эксперимента по наблюдению эффекта Комптона

Результаты наблюдения спектра рассеянного излучения показаны на рис.3. Наблюдаемое смещение не зависит от материала рассеивающего образца и длины волны λ падающего излучения, а определяется лишь углом θ между направлениями рассеянного и падающего излучений. С увеличением угла интенсивность смещённой компоненты растет, а несмещённой - падает.

Рис. 3 - Спектральный состав излучения на различных углах рассеяния θ при взаимодействии K_α-линии молибдена с кристаллом графита.

Экспериментальная часть

Экспериментальная установка, используемая в данной лабораторной работе, несколько отличается от классического опыта Комптона (рис.2). В качестве детектора рентгеновского излучения используется простой счетчик импульсов - счетчик Гейгера. Длина волны излучения рассчитывается через коэффициент пропускания алюминия, который в интересующем нас спектральном диапазоне однозначно определяется длиной волны. Работа выполняется в два этапа.

На первом этапе измеряется спектр пропускания алюминия. Схема эксперимента показана на рис.4. Монокристалл LiF с известным межплоскостным расстоянием d выполняет роль спектрального прибора: изменяя угол скольжения φ, можно наблюдать рассеянное излучение, длина волны которого определяется уравнением Брэгга-Вульфа (13). Как видно из рисунка, для этого необходимо установить счетчик Гейгера в положение, соответствующее углу рассеяния .

Рис. 4 – Схема взаимного расположения элементов для измерения спектра пропускания алюминия

Счетчик Гейгера измеряет интенсивность падающего на него излучения - количество импульсов в секунду N. Измерив спектры рассеянного излучения без алюминиевого адсорбера и с адсорбером , можно рассчитать спектр коэффициента пропускания алюминия T по формуле:

_{. (14)}

На втором этапе измеряется величина комптоновского сдвига для угла рассеивания θ=90°. Как видно из формулы (11), в этом случае разность длин волн исходного и рассеянного излучений равна комптоновской длине волны. Схема эксперимента показана на рис.5. Рассеиватель представляет собой блок из оргстекла, состоящего только из лёгких элементов - углерода, водорода и кислорода. Для получения максимальной интенсивности рассеянного излучения рассеиватель необходимо повернуть на небольшой угол (10…20°), как это показано на рисунке. Необходимо измерить интенсивность рентгеновского излучения в следующих конфигурациях:

• N₃ - интенсивность с рассеивателем, но без алюминиевого адсорбера;

• N₄ - интенсивность с рассеивателем и с алюминиевым адсорбером между источником и рассеивателем (Положение 1 на рис.5). Соответствующий коэффициент пропускания T₁ соответствует усредненной длине волны исходного рентгеновского излучения:

₍₁₅₎

• N₅ - интенсивность с рассеивателем и с алюминиевым адсорбером между рассеивателем и детектором (Положение 2 на рис.5). Соответствующий коэффициент пропускания T₂ соответствует усредненной длине волны рассеянного рентгеновского излучения:

(16)

Рис. 5 – Схема расположения элементов для исследования эффекта Комптона

В первом приближении в небольшом диапазоне длин волн зависимость коэффициента поглощения от длины волны можно считать линейной:

₍₁₇₎

При этом угловой коэффициент прямой k<0. Подставив это выражение в формулы (16) и (17) и выразив из них длины волн, можно получить выражение для комптоновского смещения:

₍₁₈₎

Внешний вид установки для исследования эффекта Комптона изображен на рис.6.

Рис. 6 – Экспериментальная установка для изучения эффекта Комптона

1 – Рентгеновская установка; 2 – гониометр; 3 – медный источник рентгеновского излучения; 4 – апертура; 5 – алюминиевый адсорбер; 6 – рассеиватель; 7 – счётчик Гейгера; 8 - блокирующий фиксатор.