Интеграл Пуассона.

Рассмотрим - если он существует.

Теперь рассмотрим этот же интеграл, только возьмем не квадратики, а окружности:

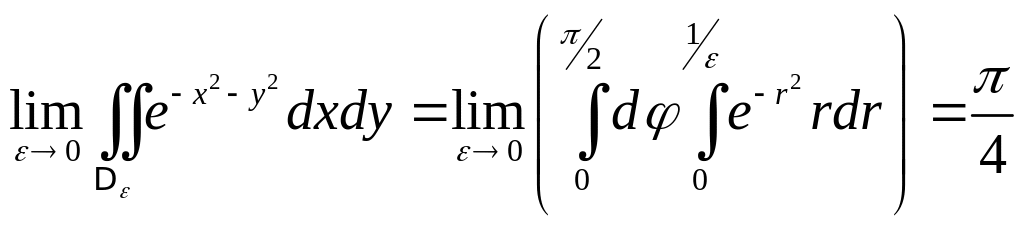
, тогда

Дифференцирование интеграла по параметру.

;

Предположим , то есть мы зафиксировали как параметр.

Если - непрерывны на , то дифференцируема на и , то есть, знаки производной и интеграла можно переставлять.

Доказательство.

Так как - непрерывна, то интеграл справа существует.

, тогда нам надо доказать, что .

- по теореме о среднем.

Доказано.

В несобственных интегралах в определенных случаях точно также можно менять местами знаки производной и интеграла.

Рассмотрим и предположим, что сходится: и имеет единственную особенность в точке , .

Тогда по критерию Коши , у нас сейчас свое для каждого , раз каждый такой интеграл сходится. Это сходимость.

- здесь уже - общее для всех . Это равномерная сходимость.

Теперь посмотрим через пределы. Рассмотрим функцию - по определению. Если мы теперь распишем определение предела (этот интеграл в предположении сходится), то получим

. Аналогично - для каждого - свое. Это сходимость.

- здесь - общее для всех . Это - равномерная сходимость.

Теорема. Критерий равномерной сходимости Вейерштрасса.

Если интеграл имеет единственную особенность в точке и , а - сходится, то - сходится равномерно на .

Доказательство.

По критерию Коши.

. Теорема доказана.

Элементы теории поля.

П усть задано некоторое множество, любому элементу поставлена в соответствие скалярная функция . Говорят, что на этом множестве задано скалярное поле.

Если мы введем систему координат . Эта функция может быть дифференцируема, тогда можно составить некоторые ее характеристики.

- мы уже доказывали, что градиент не зависит от системы координат.

Можем задать - векторное поле.

Если мы введем систему координат, то мы сможем записать , где , , . И тогда

- она тоже не зависит от системы координат.

.

Лекция 13 Криволинейные интегралы. Криволинейные интегралы первого рода.

Определение.

П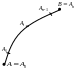 усть - измеримая кривая (т.е. имеющая конечную длину), в каждой ее точке задано скалярное поле . На каждом кусочке дуги возьмем точку . Обозначим через - максимальную длину кусочка дуги.

Составим интегральные суммы .

Если существует и он не зависит от способа разбиения и выбора точек , то он называется криволинейным интегралом первого рода по дуге функции .

Геометрический смысл.

Если , то интеграл дает длину дуги: .

Физический смысл.

Е сли - плотность, то мы точно также можем сосредоточить массу в одной точке, тогда - масса дуги, так как каждое слагаемое интегральной суммы будет давать массу кусочка дуги.

Свойства.

1) Если вместо дуги мы будем рассматривать дугу ,то интеграл не изменится, потому что каждой интегральной сумме для одной дуги соответствует интегральная сумма другой, но длина дуги не меняется и значение функции в промежуточных точках тоже.

2. Аддитивное свойство.

.

интегрируема по тогда и только тогда, когда интегрируема по и , при этом .

3. Однородные свойства – аналогичны однородным свойствам кратных интегралов.

Вычисление и существование криволинейных интегралов первого рода.

Пусть задана гладкая кривая , , , где

- непрерывно дифференцируемы и их производные не обращаются в нуль одновременно: . Пусть задана - непрерывня на , тогда - интегрируема по и .

Рассмотрим два разбиени - разбиение отрезка, а для левого интеграла у нас разбиение . Между ними есть взаимное соответствие.

1. Докажем, что .

, получается, что при

Пусть - так как эта функция непрерывна, значит это минимум достигается, кроме того, кривая гладкая, где , значит

. Получаем, что .

Первая часть доказана.

2. Рассмотрим теперь интегральные суммы, соответствующие левому и правому интегралу:

, где . Когда мы составляем эти интегральные суммы, мы берем в какой-то промежуточной точке, а когда мы считаем длину этой дуги, там появляется промежуточное значение в другой точке.

Для правого интеграла по тому же самому разбиению:

где . Под интегралом у нас стоит как раз эта функция, значит здесь у нас все вычисляется в одной и той же точке.

Докажем, что разность между ними стремится к нулю.

при

Так как существует , следовательно, существует и они равны между собой.

Пример. Вычислить массу куска параболы от точки до

, .

.