18. Криволинейные интегралы. Вычисление Криволинейные интегралы первого рода.

Определение..

П усть - измеримая кривая (т.е. имеющая конечную длину), в каждой ее точке задано скалярное поле . На каждом кусочке дуги возьмем точку . Обозначим через - максимальную длину кусочка дуги.

Составим интегральные суммы .

Если существует и он не зависит от способа разбиения и выбора точек , то он называется криволинейным интегралом первого рода по дуге функции .

Вычисление и существование криволинейных интегралов первого рода.

Пусть задана гладкая кривая , , , где

- непрерывно дифференцируемы и их производные не обращаются в нуль одновременно: . Пусть задана - непрерывня на , тогда - интегрируема по и .

Рассмотрим два разбиени - разбиение отрезка, а для левого интеграла у нас разбиение . Между ними есть взаимное соответствие.

1. Докажем, что .

, получается, что при

Пусть - так как эта функция непрерывна, значит это минимум достигается, кроме того, кривая гладкая, где , значит

. Получаем, что .

Первая часть доказана.

2. Рассмотрим теперь интегральные суммы, соответствующие левому и правому интегралу:

, где . Когда мы составляем эти интегральные суммы, мы берем в какой-то промежуточной точке, а когда мы считаем длину этой дуги, там появляется промежуточное значение в другой точке.

Для правого интеграла по тому же самому разбиению:

где . Под интегралом у нас стоит как раз эта функция, значит здесь у нас все вычисляется в одной и той же точке.

Докажем, что разность между ними стремится к нулю.

при

Пример. Вычислить массу куска параболы от точки до

, .

.

19. Криволинейный интеграл второго рода. Определение. Свойства. Физический смысл.

Определение: Пусть задана ориентировочная кривая Г на множестве L: x = x(t), y = y(t), z = z(t). Пусть на Г и на L, содержащую Г, задано векторное поле: F(x, y, z) = P(x, y, z)i + Q(x, y, z)j + R(x, y, z)k.

dL = dx*i + dy*j + dz*k; FdL = Pdx + Qdy + Rdz.

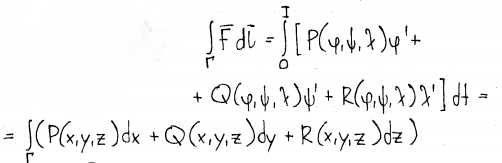
Свойства:

1) Однородность. (интеграл по области L)

∫CFdS = C ∫FdS

2) Аддитивность по области интегрирования. (интеграл от AB = AC(1) + CB(2).)

∫FdS = (1)∫FdS + (2)∫FdS

3) Аддитивность по функции интегрирования. (интеграл по области L)

∫(F(1) + F(2))dS = ∫F(1)dS + ∫F(2)dS

4) Зависимость интеграла при выборе пути интегрирования. (интеграл от AB = - интеграл от BA).

∫Pdx + Qdy = - ∫Pdx + Qdy

Физический смысл:

Пусть F(x, y) = (P(x, y), Q(x, y)) – вектор силы, действующей на материальной точку М(x, y) ориентированной кривой L. Тогда работа, совершаемая силой F(x, y)  при перемещении точки М вдоль ориентированной кривой L, равна:

A = ∫P(x, y)dx + Q(x, y)dy

20. Криволинейный интеграл 2 рода. Вычисление и существование.

1й способ – через интеграл первого рода.

Если дана гладкая кривая , , - возрастающие от к и соответствует возрастанию параметра, тогда и мы просто находим криволинейный интеграл первого рода..

2й способ.