
- •1. Мера Жордана. Измеримые множества. Примеры измеримых и неизмеримых множеств.
- •2. Критерий измеримости множества по Жордану.
- •3. Свойства измеримых множеств.
- •4. Мера криволинейной трапеции, непрерывной кривой.
- •5. Мера поверхности, заданной явно.
- •6. Кратный интеграл. Определение. Примеры вычисления интегралов по определению.
- •1)Определение:
- •2) Геометрический смысл
- •7. Суммы Дарбу
- •8. Критерий существования кратного интеграла.
- •9. Модуль непрерывности функции многих переменных. Равномерно непрерывные функции. Кратный интеграл от непрерывной функции. Равномерная непрерывность функции. Модуль непрерывности.
- •Если f – непрерывна на d – замкнутом и ограниченном множестве, то она равномерно непрерывна на d: , ) , . Так как f – непрерывна на d, то она ограничена;
- •Теорема 2 Функция непрерывная на d – измеримом замкнутом ограниченном множестве, равномерно непрерывна на нем
- •Кратный интеграл от непрерывной функции
- •10. Свойства кратных интегралов.
- •11. Вычисление кратного интеграла для прямоугольной области. Вычисление кратного интеграла в общем случае. Применение общей теоремы для вычисления двойного и тройного интегралов.
- •12. Преобразование элемента площади при замене переменныx
- •13. Замена переменных в кратном интеграле (общая теорема). Полярная замена. Цилиндрическая и сферическая замены.
- •14. Приложения кратного интеграла.
- •15. Несобственные кратные интегралы. Вычисление интеграла Пуассона.
- •16. Длина дуги кривой. Определение и вычисление. Длина дуги в полярных координатах. Длина дуги кривой, заданной в явном виде
- •Длина дуги кривой, заданной в параметрическом виде
- •Длина дуги кривой, заданной в полярных координатах
- •17. Криволинейный интеграл первого рода. Определение. Свойства. Физический и геометрический смысл.
- •18. Криволинейные интегралы. Вычисление Криволинейные интегралы первого рода.
- •19. Криволинейный интеграл второго рода. Определение. Свойства. Физический смысл.
- •20. Криволинейный интеграл 2 рода. Вычисление и существование.
- •21. Циркуляция векторного поля. Формула Грина.
- •22. Площадь поверхности. Определение. Вычисление площади поверхности, заданной в явном виде и заданной параметрически.
- •23. Поверхностный интеграл первого рода. Определение.
- •24. Ориентация поверхности. Ориентируемые и неориентируемые поверхности. Поверхностный интеграл второго рода. Определение. Физический смысл.
- •25.Поверхностный интеграл второго рода. Вычисление (2 способа)
- •26. Дивергенция. Формула Остроградского – Гаусса. Инвариантность дивергенции.
- •27. Ориентация границы поверхности. Ротор. Формула Стокса. Формула Стокса.
- •28. Потенциал поля. Условие потенциальности.
16. Длина дуги кривой. Определение и вычисление. Длина дуги в полярных координатах. Длина дуги кривой, заданной в явном виде
Пусть кривая лежит в плоскости x0y и описывается уравнением y = f(x). Для нахождения длины дуги этой кривой, заключенной между точками с абсциссами a и b, разобьем дугу на столь малые элементы, чтобы каждый из них можно было аппроксимировать прямолинейным участком (см. рисунок 1).
 Рис.
1.
Аппроксимация элемента дуги кривой
прямолинейным участком.
Рис.
1.
Аппроксимация элемента дуги кривой
прямолинейным участком.
Длину dL бесконечно малого участка можно выразить через dx и dy с помощью теоремы Пифагора:
|
|
(1) |
|
где y ' – производная функции y = f(x) по переменной x. Длина дуги равна сумме длин составляющих ее элементов:
|
|
(2) |
|
|
|
Длина дуги кривой, заданной в параметрическом виде
Пусть пространственная кривая задана уравнениями в параметрической форме:
|
|
(1) |
|
Длина пространственного отрезка описывается формулой
|
|
(2) |
|
Преобразуем это выражение, умножив и поделив его на dt:
|
|
(3) |
|
Затем разделим каждое слагаемое в числителе на знаменатель и представим результат в виде
|
|
(4) |
|
где x', y' и z' – производные функций x(t), y(t) и z(t) по переменной t. Тогда
|
|
(5) |
|
Полученная формула включает в себя формулу
|
|
(6) |
|
в качестве частного случая. Действительно, если кривая лежит в плоскости x0y, то рассматривая переменную x в качестве параметра t, мы имеем x = x, y = y(x) и z = 0. Тогда формула (5) влечет за собой формулу (6).
Длина дуги кривой, заданной в полярных координатах
Пусть
кривая лежит в плоскости x0y
и описывается уравнением r = r(φ)
в полярных координатах. Представим
выражение ![]() в
виде
в
виде
|
|
(1) |
|
Выразим декартовые координаты x и y через полярные координаты r и φ:
|
|
(2) |
|
Продифференцируем эти выражения по переменной φ:
|
|
(3) |
|
Нетрудно показать, что
|
|
(4) |
|
Следовательно,
|
|
(5) |
|
17. Криволинейный интеграл первого рода. Определение. Свойства. Физический и геометрический смысл.
Определение.
П усть
усть
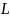 - измеримая кривая (т.е. имеющая конечную
длину), заданная на плоскости или в
пространстве. В каждой ее точке задано
скалярное поле
- измеримая кривая (т.е. имеющая конечную
длину), заданная на плоскости или в
пространстве. В каждой ее точке задано
скалярное поле
 .
На каждом кусочке дуги
.
На каждом кусочке дуги
 возьмем
точку
возьмем
точку
 .
Обозначим через
.
Обозначим через
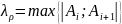 -
максимальную длину кусочка дуги.
-
максимальную длину кусочка дуги.
Составим
интегральные суммы
 .
.
Если
существует
 и
он не зависит от способа разбиения и
выбора точек
,
то он называется криволинейным интегралом
первого рода по дуге
функции
.
∫𝑓(𝑥,𝑦,𝑧)
𝑑𝑙
(𝑑𝑠)
и
он не зависит от способа разбиения и
выбора точек
,
то он называется криволинейным интегралом
первого рода по дуге
функции
.
∫𝑓(𝑥,𝑦,𝑧)
𝑑𝑙
(𝑑𝑠)
Геометрический смысл.
Если
 ,
то интеграл дает длину дуги:
,
то интеграл дает длину дуги:
 .
.
Физический смысл.
Е сли
сли
 -
плотность, то мы точно также можем
сосредоточить массу в одной точке, тогда
-
плотность, то мы точно также можем
сосредоточить массу в одной точке, тогда
 - масса дуги, так как каждое слагаемое
интегральной суммы будет давать массу
кусочка дуги.
- масса дуги, так как каждое слагаемое
интегральной суммы будет давать массу
кусочка дуги.
Свойства.
1)
Если вместо дуги
 мы
будем рассматривать дугу
мы
будем рассматривать дугу
 ,то
интеграл не изменится, потому что каждой
интегральной сумме для одной дуги
соответствует интегральная сумма
другой, но длина дуги не меняется и
значение функции в промежуточных точках
тоже.
,то
интеграл не изменится, потому что каждой
интегральной сумме для одной дуги
соответствует интегральная сумма
другой, но длина дуги не меняется и
значение функции в промежуточных точках
тоже.
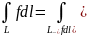
2. Аддитивное свойство.
 .
.
интегрируема
по
тогда
и только тогда, когда
интегрируема
по
 и
и
 ,
при этом
,
при этом
 .
.
Однородные свойства
Ели f, g интегрируемы на АВ, то ∫(𝑎∗𝑓+𝑏∗𝑔)𝑑𝑥=𝑎∗∫𝑓𝑑𝑥+𝑏∗∫𝑔𝑑𝑥
Если
f(x,
y,
z)
≤ g
(x,y,z),
то

Теорема о среднем f непрерывна на AB, то ∫f (x, y, z) dl≤C∫dl
Вычисление и существование криволинейных интегралов первого рода.
Пусть
задана гладкая кривая
 ,
,
 ,
,
 ,
где
,
где

 -
непрерывно дифференцируемы и их
производные не обращаются в нуль
одновременно:
-
непрерывно дифференцируемы и их
производные не обращаются в нуль
одновременно:
 .
Пусть задана
- непрерывня на
,
тогда
- интегрируема по
и
.
Пусть задана
- непрерывня на
,
тогда
- интегрируема по
и
 .
.
Рассмотрим
два разбиени - разбиение отрезка, а для левого
интеграла у нас разбиение
- разбиение отрезка, а для левого
интеграла у нас разбиение
 .
Между ними есть взаимное соответствие
(т.к. существуют непрерывные частные
производные)
.
Между ними есть взаимное соответствие
(т.к. существуют непрерывные частные
производные)
Докажем, что
 .
.

 ,
получается, что при
,
получается, что при
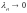

Пусть
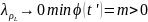 - так как эта функция непрерывна, значит
это минимум достигается, кроме того,
кривая гладкая, где
- так как эта функция непрерывна, значит
это минимум достигается, кроме того,
кривая гладкая, где
 ,
значит
,
значит
 .
Получаем, что
.
Получаем, что
 .
.
Первая часть доказана.
Рассмотрим теперь интегральные суммы, соответствующие левому и правому интегралу:
 ,
где
,
где
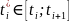 .
Когда мы составляем эти интегральные
суммы, мы берем
в
какой-то промежуточной точке, а когда
мы считаем длину этой дуги, там появляется
промежуточное значение в другой точке.
.
Когда мы составляем эти интегральные
суммы, мы берем
в
какой-то промежуточной точке, а когда
мы считаем длину этой дуги, там появляется
промежуточное значение в другой точке.
Для правого интеграла по тому же самому разбиению:
 где
где
 .
Под интегралом у нас стоит как раз эта
функция, значит здесь у нас все вычисляется
в одной и той же точке.
.
Под интегралом у нас стоит как раз эта
функция, значит здесь у нас все вычисляется
в одной и той же точке.
Докажем, что разность между ними стремится к нулю.


 при
при

Так
как существует
 ,
следовательно, существует
,
следовательно, существует
 и они равны между собой.
и они равны между собой.


 .
.

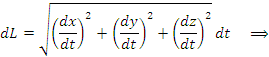
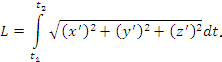
 .
. ,
,
 .
.
