12. Преобразование элемента площади при замене переменныx

v

v0+h

y C*

B C B* B*

]

v0

\

D* D*

A

u

x

D A*

u0 u0+h

=

Тогда

13. Замена переменных в кратном интеграле (общая теорема). Полярная замена. Цилиндрическая и сферическая замены.

Теорема о замене переменных.

Пусть есть , которая однозначно переводится за исключением точек границ и отображение

x=x(u,v)

y=y(u,v)

имеет непрерывные частичные производные, тогда

= , где

J=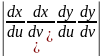

Если существует правый, существует и левый, и они равны.

Док-во: разобьём область на квадраты со стороной n, не пересекающие границы

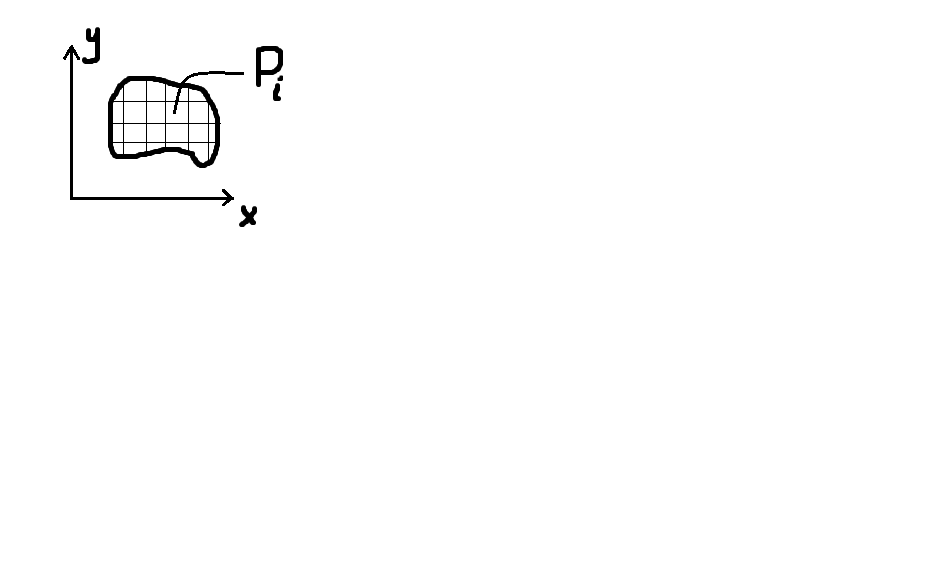
*| |= f(Pi)*|J|*

Интегральные суммы отличаются на

Полярная замена.

x = r*cosφ

y = r*sinφ

J = r

=

Обобщенно-полярная замена.

+ = 1

x = a*r*Cosφ

y = b*r*Sinφ

J = a*b*r

Цилиндрическая замена.

Сфера + параболоид

(x, y, z)  (r, φ, z)

x = r*Cosφ

y = r*Sinφ

z = z

J = r

Сферическая замена.

Сфера, полусфера, сфера + конус

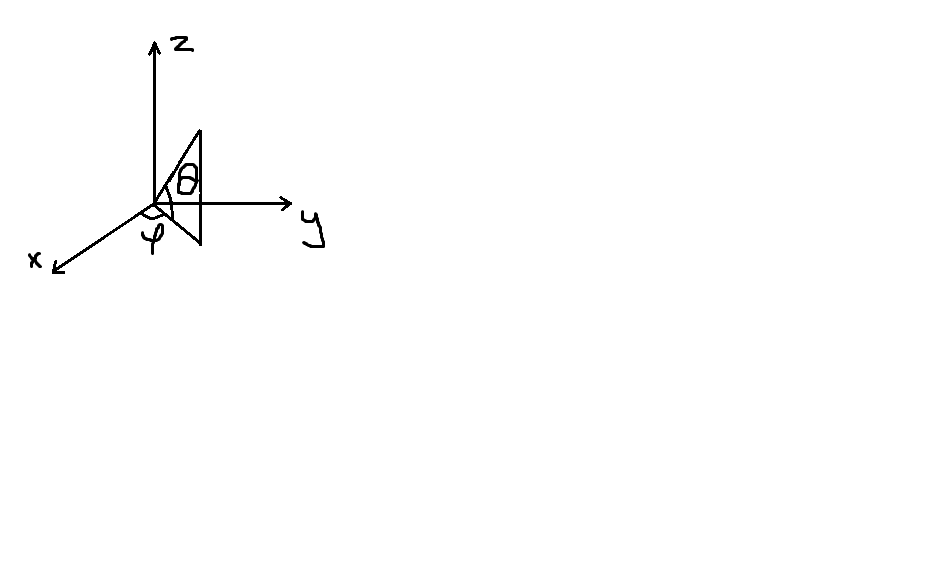
r – радиус-вектор точки

0 ≤ φ ≤ 2𝜋

≤ θ ≤

x = r*Cosθ*Cosφ

y = r*Cosθ*Sinφ

z = r*Sinθ

J = *Cosθ

14. Приложения кратного интеграла.

Двойной интеграл

Геометрические приложения:

Площадь S плоской области G выражается в декартовых прямоугольных координатах ; в криволинейных координатах , где в области Г. В частности, в полярных координатах имеем .

Если гладкая поверхность имеет уравнение , то площадь части этой поверхности , проектирующейся в область G плоскости Oxyравна

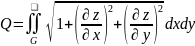
Объём V цилиндра, ограниченного сверху непрерывной поверхностью снизу плоскостью и с боков прямой цилиндрической поверхностью, вырезающей на плоскости Oxy область G, выражается интегралом .

Механические приложения:

Если пластинка занимает область G плоскости Oxy и имеет переменную поверхностную плотность , то масса М пластинки и ее статические моменты относительно осей Ox, Oy выражаются двойными интегралами , , .

Координаты центра масс определяются так: , .

Моменты инерции пластинки относительно осей Ox, Oy соответственно равны , а момент инерции пластинки относительно начала координат (полярный момент инерции) равен .

Если пластинка однородна и плотность ее не указана, условимся считать

Тройной интеграл

Объем V пространственной области Т равен .

Масса М тела с переменной плотностью , занимающего область Т:

Статические моменты тела относительно осей координат:

Координаты центра масс тела:

Моменты инерции тела относительно координатных плоскостей:

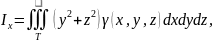
15. Несобственные кратные интегралы. Вычисление интеграла Пуассона.

Пусть функция f(x) задана в ограниченной области D. Точка x⁰ называется особой точкой функции, если в любой Ԑ окрестности точки x⁰ функция неограниченна.

Пусть D_Ԑ=D \ B_Ԑ , где B_Ԑ-открытый шар с центром в точке x⁰ и радиусом Ԑ.

Если - бесконечная область, тогда , , - интегрируема на .

Если функция f(x) имеет единственную особую точку x⁰ на области D и непрерывна на области D_Ԑ ꓯԐ >0, то несобственным интегралом функции f(x) на D называется предел

(1)

В случае существования конечного предела, несобственный интеграл сходится, а если предел не существует или равен бесконечности, то расходится.

Интеграл (1) называется абсолютно сходящимся, если сходится интеграл

Пример.

Вычисление интеграла Пуассона.

, Четная функция

Рассмотрим

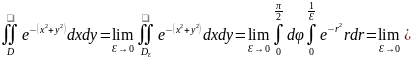
Так как функция неотрицательная, нам всё ровно по каким множествам считать.