26. Дивергенция. Формула Остроградского – Гаусса. Инвариантность дивергенции.
Пусть
есть
пространство, где задана прямоугольная
система координат
- область с кусочно гладкой границей
и на
определено поле вектора
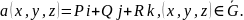(1)
Мы
будем предполагать, что
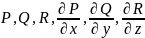непрерывны на
,
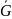откуда следует, что для вектора aимеет
смысл непрерывная функция
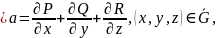(2)
называемая дивергенцией вектора a.
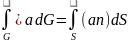(3)
Или
Это равенство называют формулой Гаусса – Остроградского.
Формула Гаусса-Остроградского говорит, что объемный интеграл от дивергенции вектора по области равен потоку вектора через границу этой области, ориентированную в направлении ее внешней нормали.
∆Доказательство:
a= (0; 0; R)
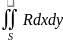– поверхностный
интеграл 2 рода.
-
верхняя граница.
-
нижняя граница.
-
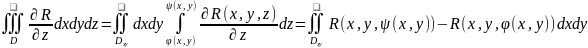двойной интеграл.
:
(
)
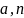= 0
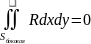– поверхностный
интеграл 2-ого рода.
▲.
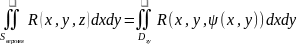
Инвариантное определение дивергенции.
След матрицы не меняется при переходе в другую ортогональную систему координат, div не меняется при переходе.
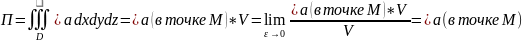
когда поверхность стягивается в точку (для потока нет системы координат).
27. Ориентация границы поверхности. Ротор. Формула Стокса. Формула Стокса.
Двойной интеграл по плоской области можно рассматривать и как поверхностный интеграл по этой поверхности. Тогда к нему можно применить формулу Грина.
-
если мы рассматриваем верхнюю сторону
поверхности.
Е
сли
мы рассмотрим противоположное направление
обхода, тогда
Далее.
Ориентация поверхности задает ориентацию проекции (см. рис).
Собственно формула Стокса.
Пусть
задана некоторая поверхность
,
гладкая, однозначно проектируемая на
все координатные плоскости, то есть ее
можно задать как:
,
,
- где эти функции непрерывно дифференцируемы.
Пусть она имеет кусочно-гладкий край
,
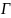ориентация которого соответствует
ориентации поверхности, пусть задано
непрерывно-дифференцируемое векторное
поле
,
непрерывно оно вплоть до границы,
дифференцируема на
без границы.
Если
мы рассмотрим
,
тогда циркуляция векторного поля
.
Слева стоит криволинейный интеграл
второго рода, справа – поверхностный
интеграл второго рода.
Доказательство.
Рассмотрим правую часть.
Пусть
единичная нормаль, которая задает
ориентацию поверхности, имеет координаты
,
тогда
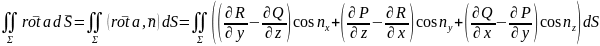
Рассмотрим
отдельно
.
Будем
проектировать эту поверхность на
,
то есть,
.
С
одной стороны нормаль имеет координаты
,
с другой стороны,
.
Тогда
,
отсюда
.
Подставляем:
-
получилась формула Грина. Это был у нас
интеграл по проекции. Посмотрим, что
это такое. Пусть у нас сам
задан параметрически:
Пусть
:
,
,
,
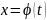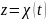где
.
Тогда
-
мы делаем такой переход исходя из формулы
для вычислений.
Аналогично,
и т.д.
Определение.
Вектор
,
компоненты которого равны соответственно
равны
;
;
называется
вихрем
или
ротором
вектора
и
обозначается:
-
rot
Определение.
Символический
вектор
называется оператором Гамильтона. ( УильямРоуан Гамильтон (1805 – 1865) – ирландский математик) Символ ∇ - “набла”.
С учетом этого обозначения можно представить себе понятие ротора вектора как векторного произведения оператора Гамильтона на вектор .
rot
Если обход по любому замкнутому контуру, лежащему на поверхности S и не пересекающему ее границы, при возвращении в исходную точку не меняет направления нормали к поверхности, то такая поверхность называется двусторонней.
Если же на поверхности S существует замкнутый контур, при обходе которого направление нормали меняется после возвращения в исходную точку на противоположное, то поверхность называется односторонней.