1. Мера Жордана. Измеримые множества. Примеры измеримых и неизмеримых множеств.

2. Критерий измеримости множества по Жордану.

3. Свойства измеримых множеств.

4. Мера криволинейной трапеции, непрерывной кривой.

5. Мера поверхности, заданной явно.

6. Кратный интеграл. Определение. Примеры вычисления интегралов по определению.

7. Суммы Дарбу. Свойства.

8. Критерий существования кратного интеграла.

9. Модуль непрерывности функции многих переменных. Равномерно непрерывные функции. Кратный интеграл от непрерывной функции.

10. Свойства кратного интеграла.

11. Вычисление кратного интеграла для прямоугольной области. Вычисление кратного интеграла в общем случае. Применение общей теоремы для вычисления двойного и тройного интегралов.

12. Преобразование элемента площади при замене переменных.

13. Замена переменных в кратном интеграле (общая теорема). Полярная замена. Цилиндрическая и сферическая замены.

14. Приложения кратного интеграла.

15. Несобственные кратные интегралы. Вычисление интеграла Пуассона.

16. Длина дуги кривой. Определение и вычисление. Длина дуги в полярных координатах.

17. Криволинейный интеграл первого рода. Определение. Свойства. Физический и геометрический смысл.

18. Криволинейный интеграл первого рода. Существование. Вычисление.

19. Криволинейный интеграл второго рода. Определение. Свойства. Физический смысл.

20. Криволинейный интеграл второго рода. Существование. Вычисление.

21. Циркуляция векторного поля. Формула Грина.

22. Площадь поверхности. Определение. Вычисление площади поверхности, заданной в явном виде и заданной параметрически.

23. Поверхностный интеграл первого рода. Определение. Вычисление для поверхности, заданной в явном виде и заданной параметрически.

24. Ориентация поверхности. Ориентируемые и неориентируемые поверхности. Поверхностный интеграл второго рода. Определение. Физический смысл.

25. Поверхностный интеграл второго рода. Вычисление (2 способа).

26. Дивергенция. Формула Гаусса-Остроградского. Инвариантность дивергенции.

27. Ориентация границы поверхности. Ротор. Формула Стокса.

28. Потенциальное поле. Критерий потенциальности. Нахождение потенциала.

1. Мера Жордана. Измеримые множества. Примеры измеримых и неизмеримых множеств.

Пусть задан прямоугольник в : . Тогда

Назовем фигурой , где - прямоугольники, которые могут пересекаться только по границам. Любую фигуру можно представить в виде такого объединения прямоугольников бесконечным числом способов, но сумма мер прямоугольников будет одна и та же. Назовем мерой сумму мер : .

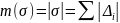Свойства меры фигуры:

1.

2. Если , то . Причем .

3. - фигуры, , , причём , если они пересекаются, быть может, только по границе.

4. фигуры, - фигура, если , то

Пусть задано ограниченное множество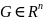 , т.е. где - некоторый прямоугольник.

Рассмотрим . Тогдачисловое множество мер ограничено сверху, т.к. , , 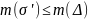значит, имеет супремум, при этом называется внутренней мерой Жордана множества G.

Числовое множество мер ограничено снизу, т.к. , значит, имеет инфимум, при этом называется внешней мера Жордана множества .

Если внутренняя и внешняя меры множества равны между собой, то множество называется измеримым и

2. Критерий измеримости множества по Жордану.

Теорема 1. Множество измеримо тогда и только тогда, когда , то есть тогда, когда фигуру, покрывающую границу, можно сделать как угодно маленькой площади.

Доказательство.

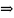Нам дано, что G – измеримо.

Его мера тогда , значит, по определению супремума и инфемума

Нам дано, что

Переходя к инфимуму в этом неравенстве

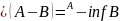
G – измеримо.

Теорема доказана.

Теорема 2. Множество G измеримо тогда и только тогда, когда .

Доказательство.

Множество G измеримо, следовательно, по теореме 1, ,

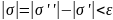- так как они могут пересекаться разве что по границе.

, следовательно .

Пусть , это означает, что .

Тогда мы берем , .

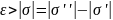
То есть мы нашли две таких фигуры, что и , следовательно, по теореме 1, G – измеримо.

Теорема 3. Множество G измеримо тогда и только тогда, когда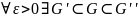 - измеримые, такие, что .

Доказательство.

Вспомним, что если , то и .

G – измеримо, значит - фигуры, а любая фигура является измеримым множеством, так как она состоит из прямоугольником, то есть нашлись нужные нам измеримые множества.

Допустим, что нашлись , тогда

переходя к инфимуму в этом неравенстве

3. Свойства измеримых множеств.

Лемма 1. Если и таковы, что , то измеримо и

Доказательство.

Поскольку мера этих множеств равна 0, то их можно поместить в , , где

, , тогда .

. Лемма доказана.

Лемма 2. Пусть , , тогда - измеримо, .

Доказательство:

заключаем в , тогда в ней же и содержится, получаем, что .

Лемма доказана.

Теорема 1. Если - измеримо, то множества - измеримы.

Доказательство.

Поскольку множества измеримы, то . Кроме того, .

по лемме 1. Мы получили, что граница содержится в множестве, мера которого равна 0, тогда по лемме 2 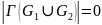. Значит, по теореме 2 - измеримо. Точно также и далее все то же самое.

Теорема 2. Пусть G – измеримо. Если мы рассечем его с помощью множества меры 0 на 2 непересекающиеся части, то их части тоже будут измеримы.

Доказательство.

Очевидно, что . Тогда по лемме 2 множество измеримо, аналогично для .

Теорема доказана.

Теорема 3. Пусть - измеримые, пересекаются разве что по границе.

, тогда мы уже доказали, что - измеримое множество. При этом

.

Доказательство.

Возьмем такие, что

И точно также , такие, что . Тогда .

Раз множества пересекаются разве только по границе, то тоже пересекаются разве что по границе,

Про мы можем лишь сказать, что .

Мы хотим доказать, что . Причем, что это множество измеримо, доказано в предыдущей теореме.

Возьмем таким образом, что . Если множество измеримо, то найдется такое , что .

Соответственно найдется

Тоже самое можно сказать про :

У нас было доказано, что раз у нас и пересекаются разве что только по границе, то и могут тоже пересекаться только по границе, тогда для них .

А про и мы такого сказать не можем (см. рисунок), мы лишь можем написать

. Тогда мы получаем, кроме всего прочего, что

, получаем строчку неравенств:

Таким образом, мы нашли два множества, и :

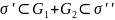
Если мы возьмем теперь супремум и инфемум, то у нас получится, что внутренняя мера нашего объединения больше, чем . Внешняя мера меньше, чем , отсюда следует, что они равны между собой. Что и требовалось доказать.

Следствие.

Если - измеримые, а , то

Доказательство:

Что разность измерима, мы уже доказали, докажем теперь равенство:

. Следствие доказано.