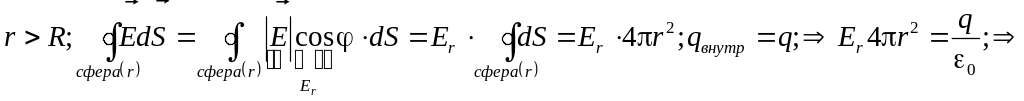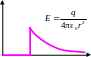Лекция 11. Потенциал электростатического поля
Лекция 11. Потенциал электростатического поля
§11.1. Теорема Гаусса
Поток вектора
► Потоком вектора
![]() через элементарную площадку
через элементарную площадку
![]() называется скалярная величина
называется скалярная величина
![]() ,
где α
– угол между вектором
и нормалью к площадке.
,
где α
– угол между вектором
и нормалью к площадке.
► 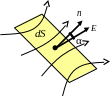 Физический
смысл потока напряжённости электрического
поля: численно
равен числу силовых линий, проходящих
через эту поверхность.
Физический
смысл потока напряжённости электрического
поля: численно
равен числу силовых линий, проходящих
через эту поверхность.
Действительно, модуль вектора напряжённости эл. поля пропорционален «густоте» линий, т.е. их числу, приходящемуся на перпендикулярную площадку. cosα учитывает неперпендикулярность площадки.
Введём вектор
![]() .
Т.е. вектор:
.
Т.е. вектор:
Перпендикулярный элементу поверхности
По величине равный его площади dS,
Замечание: Вектор
![]() замкнутой поверхности всегда направлен
«вовне».
замкнутой поверхности всегда направлен
«вовне».
► Поток вектора через
элементарную поверхность:
![]()
► Поток через
произвольную поверхность:
![]()
► Теорема Гаусса для напряжённости электрического поля (интегральная форма):
![]()
Замечания:
Теорема Гаусса является следствием закона Кулона
 .
При любой степени кроме «-2» она не
выполняется. Теорема Гаусса –
следствие трёхмерности пространства.
.
При любой степени кроме «-2» она не
выполняется. Теорема Гаусса –
следствие трёхмерности пространства.Теорема Гаусса в дифференциальной форме:
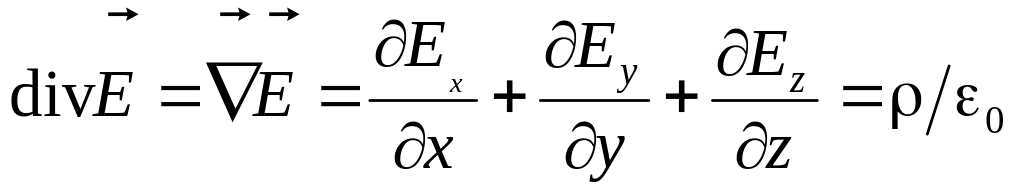 .
Перевод с языка символов: «Источником
электрического поля являются электрические
заряды»
.
Перевод с языка символов: «Источником
электрического поля являются электрические
заряды»
§11.2. Применение теоремы Гаусса для вычисления напряженности поля
Поле заряженной сферы (Иродов, §1.3, пример 5)
(материал, разбирается на семинаре)
С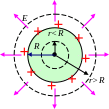 ферическая
поверхность радиуса R
заряжена зарядом q.
Найти
.
ферическая
поверхность радиуса R
заряжена зарядом q.
Найти
.
Обозначения:
 – радиус-вектор, проведённый из центра
сферы
– радиус-вектор, проведённый из центра
сферы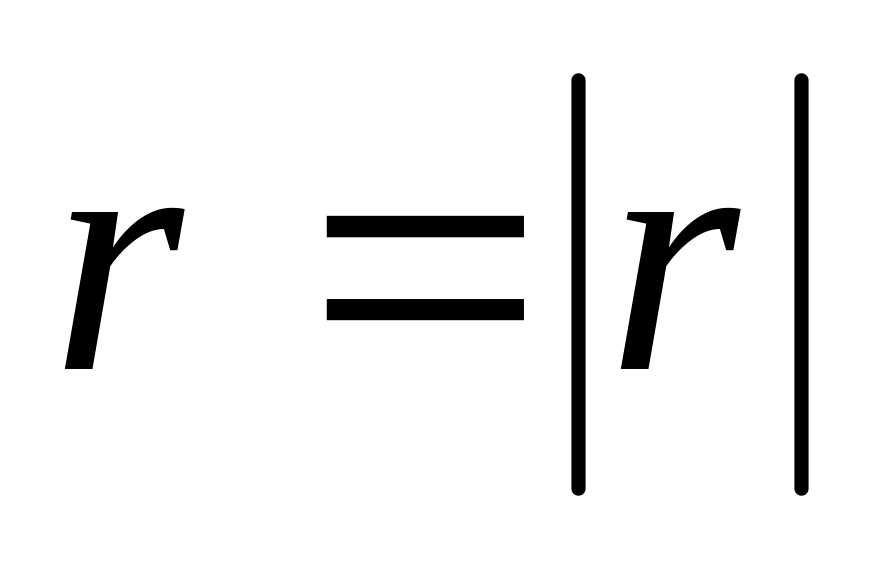 – расстояние от точки до центра сферы
– расстояние от точки до центра сферы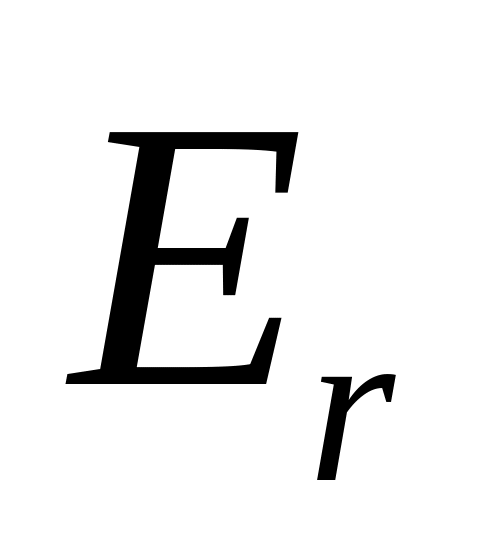 – проекция вектора напряжённости на
радиус-вектор
– проекция вектора напряжённости на
радиус-вектор
Из соображений симметрии: 1)
![]() 2)
2)
![]()
Т.е. это центральное поле. Очевидно,
что в качестве Гауссовой поверхности
удобно выбрать сферу радиуса r,
концентрическую с заряженной сферой.
Теорема Гаусса:
![]() .
Заряженная сфера разбивает пространство
на 2 области. Рассмотрим это уравнение
в каждой из областей:
.
Заряженная сфера разбивает пространство
на 2 области. Рассмотрим это уравнение
в каждой из областей:
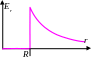
Итог:![]() – поле заряженной сферы
– поле заряженной сферы
Замечание: При
![]() формула совпадает с полем точечного
заряда
формула совпадает с полем точечного
заряда
Поле шара, заряженного по объёму (Иродов §1.3, пример 6)
(материал, разбирается на семинаре)
Условие: Шар радиуса R равномерно заряжен по объёму зарядом q. Найти .
Это также случай сферической симметрии
и в качестве гауссовой поверхности
будем брать сферу. Кроме того, вне шара
напряжённость будет точно такой же, как
и вне заряженной сферы. Внутри шара
напряжённость будет другой. Объёмная
плотность заряда:
![]() .
.
Применим теорему Гаусса к сфере радиуса
![]() :
:
![]()
И тог:
тог:![]() – поле объёмно заряженного шара
– поле объёмно заряженного шара
Бесконечная заряженная нить
Условие: бесконечная нить равномерно заряжена с линейной плотностью λ. Найти .
Обозначения: радиус-вектор и расстояние отсчитываются от нити.
Из соображений симметрии: 1) 2)
Гауссова поверхность – цилиндр радиуса r и высоты h. Теорема Гаусса: .
![]()
![]()
![]() – поле заряженной нити.
– поле заряженной нити.
Бесконечный полый цилиндр (Иродов §1.3, пр 4)
У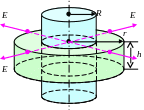 словие:
бесконечный полый цилиндр радиуса R
равномерно заряжен с поверхностной
плотностью σ.
Найти
.
словие:
бесконечный полый цилиндр радиуса R
равномерно заряжен с поверхностной
плотностью σ.
Найти
.
Итог:
![]() –
поле заряженного цилиндра
–
поле заряженного цилиндра
П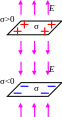 оле
бесконечной заряженной плоскости
Иродов §1.3, пр.2
оле
бесконечной заряженной плоскости
Иродов §1.3, пр.2
(материал, разбирается на семинаре)
Из соображений симметрии очевидно:
Вектор напряжённости перпендикулярен плоскости
На одинаковом расстоянии от плоскости сверху и снизу напряжённость одинакова по величине и противоположна по направлению:
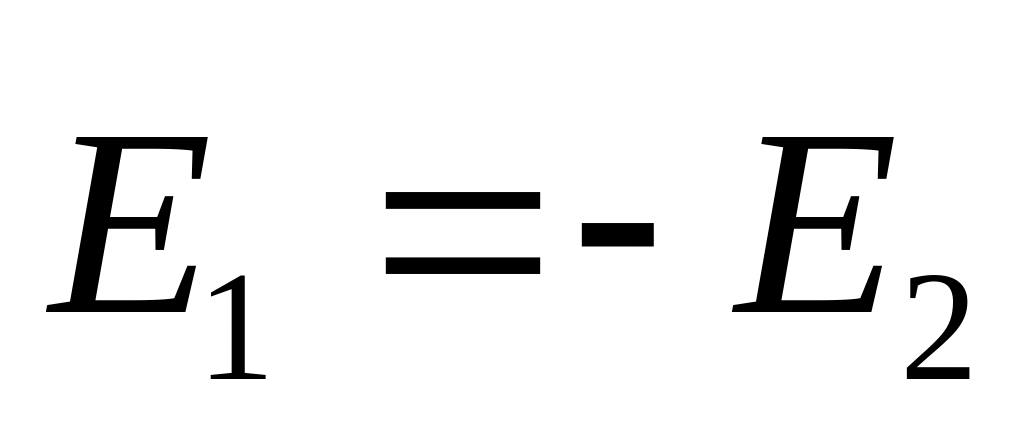
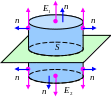
Гауссова поверхность: цилиндр с основаниями, равноудаленными от плоскости.
Теорема Гаусса:
![]()
![]()
![]()
![]()
На боковой поверхности:![]() Собираем вместе:
Собираем вместе:
![]()
![]() – Поле заряженной плоскости.
– Поле заряженной плоскости.
З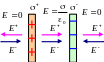 амечания:
амечания:
Поле не зависит от расстояния до плоскости – она бесконечна.
Поле плоского конденсатора. Две плоскости, заряжены одинаково по величине и противоположно по знаку. Поле внутри пластин удваивается, а вне пластин уничтожается (см. рис.).
Конфигурации зарядов для применения теоремы Гаусса
Симметрия |
dim=0 ÷ 1 |
dim=2 |
dim=3 |
Сферическая |
Точечный заряд
|
Сфера
|
Шар
|
Цилиндрическая |
Нить
|
Полый цилиндр
|
Объёмный цилиндр
|
Плоскостная |
– |
Плоскость
|
Пластинка
|
§11.3 Работа электрического поля. Потенциал
Точечный заряд q движется в поле неподвижного точечного заряда q0. Найти работу сил поля.
Определение работы:
![]() .
Сила электростатическая:
.
Сила электростатическая:
![]()
![]()
Поле создаёт точечный заряд q0:
![]() .
На рис. видно:
.
На рис. видно:
![]() .
На столько на участке длины dl
уменьшается расстояние до заряда q0.
Т.о.:
.
На столько на участке длины dl
уменьшается расстояние до заряда q0.
Т.о.:
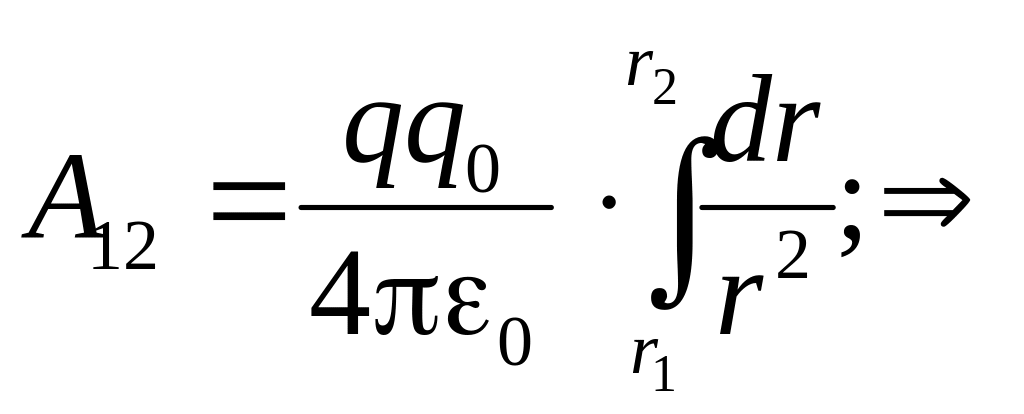
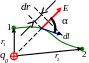
![]() (*)
(*)
Мы считали, что поле создаётся точечным зарядом. Но вывод справедлив и для произвольной конфигурации зарядов, т.к. по принципу суперпозиции она эквивалентна сумме точечных зарядов.
Следствия
Работа электрического поля не зависит от траектории.
Работа электрического поля по замкнутому контуру равна нулю
![]()
![]() – теорема о циркуляции электростатического
поля
– теорема о циркуляции электростатического
поля
Электростатическое поле консервативно (следует из 1 и 2). Для него можно ввести потенциальную энергию:
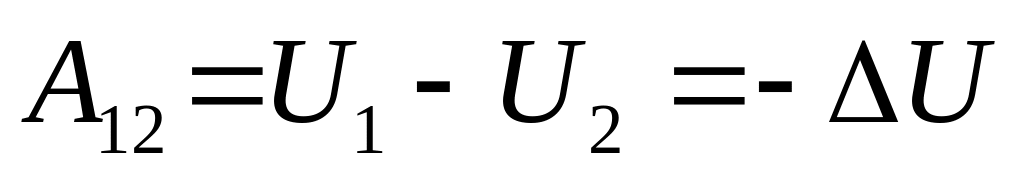 .
Однако, для электрического поля удобно
выделить перемещаемый заряд q
и вместо энергии используют другую
характеристику поля – потенциал
φ:
.
Однако, для электрического поля удобно
выделить перемещаемый заряд q
и вместо энергии используют другую
характеристику поля – потенциал
φ:
![]() (**)
(**)
Потенциал точечного заряда. Сравним формулы (*) и (**). Тогда поле точечного заряда:
![]() ;
;
Для устранения константы достаточно задать потенциал для одной произвольной точки:
![]()
![]() – Потенциал точечного заряда
– Потенциал точечного заряда
Потенциал точки равен работе по перемещению в неё единичного заряда из бесконечности
Действительно:
![]()
![]()
Связь напряжённости и потенциала
|
Общая формула |
Сферическая и осевая симм.:
|
Плоская симметрия:
|
Дано:
|
|
|
|
Дано: . Найти |
|
|
|
Преимущества метода потенциала
Лёгкость расчёта работы и энергии
Рассчитать напряжённость поля по формуле
 гораздо проще, чем рассчитывать три
компоненты вектора непосредственно с
помощью интегрирования по принципу
суперпозиции
гораздо проще, чем рассчитывать три
компоненты вектора непосредственно с
помощью интегрирования по принципу
суперпозиции
![]()
Эквипотенциальная поверхность:
множество точек с координатами
![]()
§11.4. Электрический диполь
П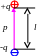 ри
вычислении полей различных конфигураций
зарядов при
ри
вычислении полей различных конфигураций
зарядов при
![]() мы всегда получали поле точечного заряда
мы всегда получали поле точечного заряда
![]() .
Однако, в случае
.
Однако, в случае
![]() эта формула даёт 0, хотя поле на больших
расстояниях нулю не равно. Это означает,
что данное приближение слишком грубое.
эта формула даёт 0, хотя поле на больших
расстояниях нулю не равно. Это означает,
что данное приближение слишком грубое.
Электрический диполь – система из 2-х одинаковых по модулю разноимённых зарядов.
Дипольным моментом диполя называется
вектор
![]() ОТ «-» К «+»!
ОТ «-» К «+»!
Потенциал диполя
В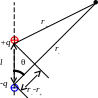 ыберем
некоторую точку на большом расстоянии
от диполя (см. рисунок) и вычислим
потенциал, создаваемый диполем в этой
точке:
ыберем
некоторую точку на большом расстоянии
от диполя (см. рисунок) и вычислим
потенциал, создаваемый диполем в этой
точке:
![]() .
.
При
![]() :
:
![]()
![]() – потенциал диполя
– потенциал диполя
Угол θ – угол между дипольным моментом и направлением на точку. Частные случаи:
Потенциал на оси диполя:


Потенциал на перпендикуляре:
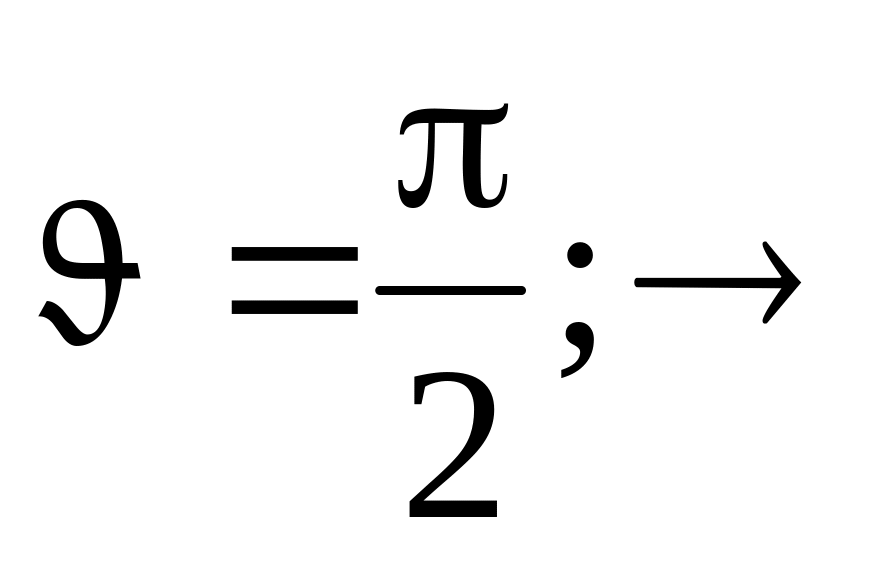

Напряжённость электрического поля диполя
(без док-ва):
![]() – поле диполя
– поле диполя
Порекомендовать попытаться получить это выражение самим в декартовой системе координат.
Замечание: У точечного заряда
![]() .
Поле диполя
.
Поле диполя
![]() спадает на расстоянии значительно
быстрее, т.к. разноимённые заряды диполя
частично компенсируют друг друга. Вывод:
разговоры о диполях имеют смысл, только
если суммарный заряд системы равен
нулю. Если есть некомпенсированный
заряд, он забьёт дипольный момент.
спадает на расстоянии значительно
быстрее, т.к. разноимённые заряды диполя
частично компенсируют друг друга. Вывод:
разговоры о диполях имеют смысл, только
если суммарный заряд системы равен
нулю. Если есть некомпенсированный
заряд, он забьёт дипольный момент.
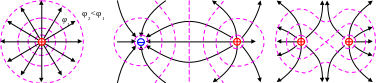
Можно представить себе, как выглядят силовые линии диполя (см. рис.)
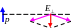


Диполь во внешнем электрическом поле
Е сли
поместить электрический диполь во
внешнее электрическое поле, то на
положительный и отрицательный заряды
будут действовать силы
сли
поместить электрический диполь во
внешнее электрическое поле, то на
положительный и отрицательный заряды
будут действовать силы
![]() и
и
![]() ,
равные по величине и направленные в
противоположные стороны. Вычислим
момент этих сил относительно центра
масс диполя:
,
равные по величине и направленные в
противоположные стороны. Вычислим
момент этих сил относительно центра
масс диполя:
![]()
![]()
![]()
![]()
§15.5. Дифференциальный оператор набла
(дополнительный материал, разбирается на консультации)
![]() – Оператор набла (оператор Гамильтона)
– векторный дифференциальный оператор.
Введен Гамильтоном и назван наблой по
сходству с древнееврейским музыкальным
инструментом.
– Оператор набла (оператор Гамильтона)
– векторный дифференциальный оператор.
Введен Гамильтоном и назван наблой по
сходству с древнееврейским музыкальным
инструментом.
В Декартовых координатах:
![]()
Действия с оператором набла
Градиент: умножение на скаляр:
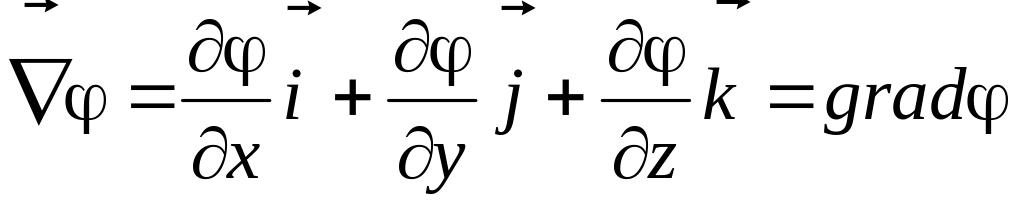 .
.
Результирующий вектор направлен в сторону быстрейшего возрастания функции.
Дивергенция (источник): Скалярное умножение на вектор:
 .
.Ротор (вихрь): векторное умножение на вектор:
 .
.
Операции второго порядка
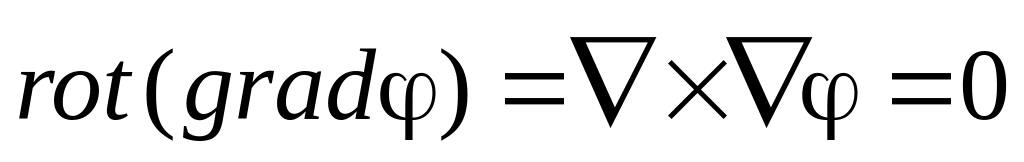
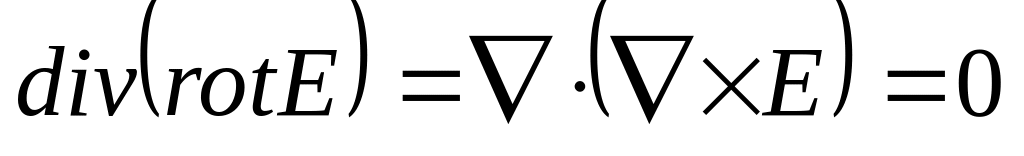
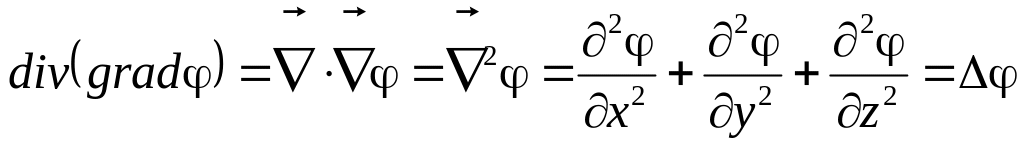 .
Это оператор Лапласа (Лапласиан).
.
Это оператор Лапласа (Лапласиан). .
Действия с оператором набла аналогичны
действиям с обычными векторами. В данном
случае можно воспользоваться известной
формулой для двойного векторного
произведения «бац минус цаб»:
.
Действия с оператором набла аналогичны
действиям с обычными векторами. В данном
случае можно воспользоваться известной
формулой для двойного векторного
произведения «бац минус цаб»: .
Тогда:
.
Тогда:
![]() ,
где
,
где
![]()
Литература
Л-3. И. Е. Иродов. Электромагнетизм. Основные законы: Учеб. пособие для вузов. – М.: Бином. Лаборатория базовых знаний, 2006.
Л-9. И. В. Савельев. Курс общей физики: Учеб. пособие для вузов: В 5-ти кн.. Кн. 2 : Электричество и магнетизм / Савельев И.В.. - М. : Астрель : АСТ, 2007. - 336 с.
11-