По правилу сложения матриц

,

аксиома 4 имеет место.

Итак, аксиомы 1 - 4 справедливы. Аналогично проверяется выполнение аксиом 5 - 8. Таким образом, совокупность всех квадратных матриц 2-го порядка - линейное пространство.

Следует отметить, что, вводя линейное пространство, мы отвлекаемся не только от конкретной природы изучаемых объектов, но и от конкретных правил образования суммы векторов и произведения на число, - важно лишь, чтобы эти правила удовлетворяли аксиомам, сформулированным в определении линейного пространства.

Укажем некоторые следствия из аксиом.

1. Единственность нулевого элемента.

Действительно, допустим, 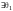и 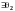- нулевые элементы, следовательно, .

Имеем (так как - нулевой), но (так как - нулевой), следовательно, .

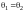2. Единственность противоположного элемента.

Пусть и , - противоположные элементы для , т.е. , .

Рассмотрим вектор . Имеем

.

С другой стороны,

.

Теперь всюду далее противоположный элемент для будем обозначать .

3. Существование и единственность разности.

Дадим определение разности. Для любых двух векторов и назовем разностью и такой вектор , что . Обозначим .

Положим .

Имеем

.

Следовательно, вектор удовлетворяет определению разности.

Покажем, что он единственный вектор, удовлетворяющий этому определению.

Пусть .

К обеим частям последнего равенства прибавим вектор :

-

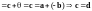таким образом, вектор - единственный.

4. Для любого вещественного числа .

5. Для любого вектора .

6. Если , то либо , либо .

Для любого вещественного числа и любого справедливы соотношения:

7. ;

8. .

Билет 14. Базис линейного пространства. Примеры базисов в конкретных пространствах.

Определение 2. Пусть - линейное пространство. Вектор называется линейной комбинацией векторов , если найдутся такие числа , что

.

Определение 3. Система векторов , принадлежащих линейному пространству , называется линейно зависимой, если найдутся такие числа , не все равные нулю одновременно, что выполняется равенство

.

Определение линейно зависимой системы векторов можно дать в следующей эквивалентной форме, иногда более удобной.

Определение 3'. Система векторов , принадлежащих линейному пространству , называется линейно зависимой, если один из векторов является линейной комбинацией остальных.

Определение 4. Система векторов , принадлежащих линейному пространству , называется линейно независимой, если из равенства

следует, что .

Пример 3. Пусть - линейное пространство всех матриц порядка . Доказать, что векторы

и

линейно независимы.

Решение. Рассмотрим линейную комбинацию :

. (10.1)

Привлекая правила умножения матриц на число и сложения матриц, получим

. (10.2)

Равенства (10.1) и (10.2) дают

откуда , следовательно, и линейно независимы.

Справедливы следующие два утверждения, доказательство которых приведено в лекции 1.

Теорема 1. Всякая система векторов, содержащая нулевой вектор, линейно зависима.

Теорема 2. Всякая система векторов 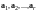, содержащая линейно зависимую подсистему векторов, , линейно зависима.

Определение 5. Система векторов линейного пространства называется базисом в , если:

1) линейно независима;

2) (вещественные числа):

. (10.3)

Правая часть равенства (10.3) называется разложением вектора по базису , а числа - координатами вектора в базисе .

Приведем примеры базисов в конкретных линейных пространствах.

Пример 4. - линейное пространство всех геометрических векторов, базисом являются любые три некомпланарных вектора.

Пример 5. - линейное пространство всех многочленов степени . Показать, что базисом является система векторов .

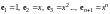Решение. Составим линейную комбинацию векторов и приравняем ее нулевому вектору:

,

или

.

Имеет место основная теорема алгебры: всякий многочлен степени с действительными коэффициентами имеет ровно корней, при этом каждый корень считается столько раз, какова его кратность. Это утверждение означает, что равенство возможно не более, чем в точках, т.е. не может выполняться тождественно (как равенство между векторами в ).

Следовательно, допущение, что линейная комбинация векторов с коэффициентами равна нулевому вектору , влечет , а это означает, что линейно независимы.

Пусть - произвольный многочлен степени . В последней записи представлен в виде линейной комбинации векторов , что вместе с линейной независимостью этих векторов доказывает, что система - базис в пространстве многочленов степени (в соответствии с определением 5).

Пример 6. - линейное пространство всех квадратных матриц порядка 2. Показать, что базисом является система

, , , .

Решение. Убедимся в том, что система линейно независима. Составим линейную комбинацию и приравняем ее :

,

или

,

откуда

.

Последнее равенство дает , следовательно, система векторов линейно независима.

Пусть - произвольный вектор из .

Привлекая определения сложения матриц и умножения матрицы на число, получим

,

т.е. любой вектор из можно представить в виде линейной комбинации . В соответствии с определением 5 это вместе с доказанной выше линейной независимостью означает, что - базис.