Билет 30. Ортогональные матрицы, их свойства (доказать: q является ортогональной тогда и только тогда, когда столбцы q составляют ортонормированную систему).

Определение 7. Квадратная матрица называется ортогональной, если

.

Пример 5. В линейном пространстве всех геометрических векторов плоскости матрица линейного оператора поворота на угол против часовой стрелки имеет вид

.

Для нее , и, следовательно, - ортогональная матрица.

Отметим некоторые свойства ортогональной матрицы.

Утверждение 1. Квадратная матрица является ортогональной тогда и только тогда, когда ее столбцы составляют ортонормированную систему арифметических векторов.

Доказательство. Необходимость. Пусть , , ортогональна.

Имеем

, .

В соответствии с правилом умножения матриц , , где

. (13.8)

Так как ортогональна, то , и, следовательно,

(13.9)

Равенства (13.8) и (13.9) означают, что строки матрицы , рассматриваемые как арифметические n-мерные векторы, составляют ортонормированную систему, необходимость тем самым доказана.

Достаточность. Пусть строки матрицы составляют ортонормированную систему арифметических векторов. Тогда в соответствии с введенными выше обозначениями (см. (13.8))

Но это означает, что и, следовательно, (в силу единственности обратной матрицы) и ортогональна.

Билет 31. Ортогональные матрицы, их свойства (доказать: матрица перехода от ортонормированного базиса к ортонормированному базиса является ортогональной).

Утверждение 2. Матрица перехода от ортонормированного базиса евклидова пространства к любому другому его ортонормированному базису является ортогональной.

Доказательство. Пусть (I) и (II) – два ортонормированных базиса в . , , - матрица перехода от (I) к (II).

В соответствии с определением матрицы перехода от базиса к базису справедливо равенство

,

или

, . (13.10)

Так как (II) – ортонормированный базис, то

Используя (13.10), получаем

а это означает, что столбцы матрицы составляют ортонормированную систему. Привлекая утверждение I, заключаем, что - ортогональная матрица.

Билет 32.

Ортогональные матрицы, их свойства (доказать: если Q ортогональная то Q^T ортогональная).

Билет 33.

Ортогональные операторы в евклидовом пространстве, их свойства.

Утверждение 2. Матрица перехода от ортонормированного базиса евклидова пространства к любому другому его ортонормированному базису является ортогональной.

Теорема 2. В евклидовом пространстве всякая система ненулевых ортогональных векторов линейно независима.

Определение 8. Линейный оператор в евклидовом пространстве называется ортогональным, если

(оператор сохраняет норму любого вектора).

Пример 6. Евклидово пространство 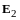- пространство всех геометрических векторов плоскости, скалярное произведение введено равенством , - оператор поворота на угол против хода часовой стрелки. Оператор - ортогональный.

В самом деле, оператор - линейный, так как из геометрических соображений ясно, что - действительного числа , . А так как при повороте длина любого вектора сохраняется, то - ортогональный оператор.

Теорема 4. Пусть - евклидово пространство, - ортогональный оператор в . Тогда

( сохраняет скалярное произведение).

Доказательство. Пусть , , рассмотрим .

Имеем

. (13.11)

С другой стороны,

. (13.12)

Сравнивая (13.11) и (13.12) заключаем, что .

Теорема доказана.

Теорема 5. Пусть - евклидово пространство, (I) - ортонормированный базис, - ортогональный оператор в . Тогда система векторов 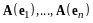(II) - ортонормированный базис.

Доказательство. Имеем

и, следовательно, - ортонормированная система. Но тогда , и по теореме 2 система (II) линейно независима, а так как , (II) – базис, и по доказанному – ортонормированный.

Теорема доказана.

Теорема 6. Пусть - евклидово пространство, - ортогональный оператор в . Тогда в любом ортонормированном базисе задается ортогональной матрицей.

Доказательство. Пусть (I) – произвольный ортонормированный базис в . Тогда система векторов (II) – тоже ортонормированный базис (теорема 5).

Пусть - матрица оператора в базисе (I).

В соответствии с определением матрицы оператора (определение 3 в лекции 12) справедливо следующее равенство:

и, следовательно, матрица является матрицей перехода от базиса (I) к базису (II) (см. равенства (11.1) в лекции 11). Тогда в силу доказанного выше утверждения 2 матрица является ортогональной.

Теорема доказана.

Определение 9. Линейный оператор в евклидовом пространстве называется самосопряженным (симметрическим), если

.

Пример 8. Пусть - произвольное евклидово пространство, - некоторое действительное число. Положим .

Справедливо равенство

,

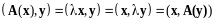и, следовательно, - симметрический.

Отметим некоторые свойства симметрического оператора.

Определение 10. Матрица , , называется симметрической, если .

Теорема 7. Пусть - евклидово пространство, (I) - ортонормированный базис в , - симметрический оператор в . Тогда матрица оператора в (I) симметрическая.

Доказательство. Пусть , - матрица оператора в (I). В соответствии с определением матрицы оператора справедливы следующие равенства:

,

,

…………………………………….. ... (13.13)

.

Воспользовавшись соотношениями (13.13), получим

. (13.14)

. (13.15)

Так как - симметрический оператор, .

Сравнивая (13.14) и (13.15), находим, что , и матрица - симметрическая.

Теорема доказана.

Теорема 8. Если линейный оператор , определенный в евклидовом пространстве , задается хотя бы в одном ортонормированном базисе симметрической матрицей, оператор - симметрический.

Доказательство. Пусть - линейный оператор в евклидовом пространстве , (I) – произвольный ортонормированный базис в , , - матрица оператора в базисе (I) (т.е. справедливы равенства (13.13)), - симметрическая, или .

Пусть , . Так как (I) – базис, найдутся числа и такие, что , .

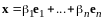Имеем

, (13.16)

. (13.17)

Используя равенства (13.16) и (13.17) и условие, что (I) – ортонормированный базис, получим

,

.

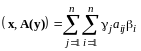Так как симметрическая, и , а это означает, что оператор симметрический.

Теорема доказана.

Приведем без доказательства еще одно свойство самосопряженного оператора.

_{Теорема 9.} Пусть - евклидово пространство, - линейный оператор в . Оператор является симметрическим тогда и только тогда, когда в существует ортонормированный базис, составленный из собственных векторов оператора

Определение 8. Пусть - линейное пространство, - линейный оператор в . Вектор называется собственным вектором оператора , если найдется действительное число такое, что

.

Число называется собственным значением, соответствующим данному собственному вектору ..