Билет 28. Процесс ортогонализации Шмидта.

Опишем процесс построения ортогонального базиса в линейной оболочке любых линейно независимых векторов.

Пусть линейно независимы.

Шаг 1. Примем .

Шаг 2. Примем . Отметим, что , так как является линейной комбинацией и , причем и линейно независимы (линейная комбинация векторов и с коэффициентами, один из которых, а именно коэффициент при , заведомо отличен от нуля, не может равняться ).

Подберем так, чтобы :

и .

Шаг 3. Примем . Отметим, что , так как является линейной комбинацией , и , а эти векторы линейно независимы. Подберем и так, чтобы и .

Отсюда

, .

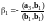Шаг 4. Пусть уже построена ортогональная система ненулевых векторов , причем , является линейной комбинацией векторов . Положим

.

Вектор , так как является линейной комбинацией линейно независимых векторов с коэффициентами, один из которых, а именно коэффициент при , заведомо отличен от нуля (поскольку не входит в ).

Коэффициенты подберем так, чтобы был ортогонален векторам :

.

Отсюда

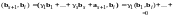
и

, .

Продолжая процесс, построим ортогональную систему векторов , причем , , 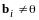откуда в силу теоремы 2 следует, что линейно независимы. Линейная оболочка векторов является подпространством размерности ( ), а это означает, что - базис в (по построению - ортогональный).

Описанный выше процесс носит название процесса ортогонализации Шмидта.

Пример 3. - евклидово пространство геометрических векторов. Применяя процесс ортогонализации Шмидта, построить ортогональный базис в подпространстве, натянутом на векторы и .

Полагаем

, .

П одбираем :

,

откуда .

Итак, , и базис в линейной оболочке составляют векторы , .

Геометрический смысл процедуры иллюстрирует рис. 13.1. Подпространство , натянутое на векторы , - плоскость, проходящая через и векторы и , приведенные к точке . В этой плоскости построен базис , 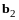такой, что .

Билет 29. Ортогональные и ортонормированные базисы в евклидовом пространстве.

Определение 5. Вектор 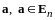называется нормированным, если .

Если , то нормированием называется переход к вектору ( является нормированным, так как и, следовательно, ).

Определение 6. Система векторов в евклидовом пространстве 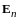называется ортонормированной системой, если

Всякое евклидово пространство обладает ортонормированными базисами.

В самом деле, ранее было показано, что всякое евклидово пространство обладает ортогональными базисами. Возьмем в произвольный ортогональный базис и нормируем все его векторы, т.е. перейдем к системе векторов

. (13.7)

Система (13.7) - ортонормированный базис в .

Пример 4. - евклидово пространство геометрических векторов. Указать какой-нибудь ортонормированный базис в линейной оболочке векторов и .

В примере 3 был построен ортогональный базис , в .

Имеем

, ,

, .

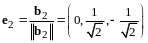Векторы - ортонормированный базис в .

Теорема 3. Пусть - евклидово пространство, (I) – базис в . Базис является ортонормированным тогда и только тогда, когда для любых векторов , , , скалярное произведение выражается равенством

.

Доказательство. Необходимость. Пусть базис (I) – ортонормированный, т.е.

Тогда .

Но во внутренней сумме всего одно слагаемое отлично от нуля при ( ). Таким образом, .

Достаточность. Пусть базис (I) таков, что 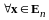, . Для векторов базиса справедливы разложения

,

.

В силу этих разложений получим , , – и базис (I) – ортонормированный.