Алгебра и геометрия / Ресурсы / Lektsii_po_linal_i_anGeom

Министерство образования и науки Российской Федерации Федеральное агентство по образованию

Московский государственный институт электронной техники

(технический университет)

Е.В. Ржавинская, Т.А. Олейник, Т.В. Соколова

Лекции по линейной алгебре и аналитической геометрии

Учебное пособие

Утверждено редакционно-издательским советом института

Москва 2007

УДК 512.8

Л43

Рецензенты: канд. физ.-мат. наук, проф. А.М. Ревякин;

канд. физ.-мат. наук, доц. О.Ю. Агарева

Ржавинская Е.В., Олейник Т.А., Соколова Т.В.

Л43 Лекции по линейной алгебре и аналитической геометрии:

Уч. пособие. – М.: МИЭТ, 2007. – 200 с.: ил.

ISBN 978-5-7256-0466-5

Содержание пособия представляет собой курс линейной алгебры и аналитической геометрии, соответствующий действующим в настоящее время образовательным стандартам.

В лекциях 1 – 5 кратко излагаются элементы аналитической геометрии. Лекции 6 и 7 посвящены определителям и матрицам. Лекции 8 и 9 – системам линейных уравнений. В

лекциях 10 – 13 рассматриваются линейные пространства и линейные операторы,

действующие в них. Лекция 14 знакомит с квадратичными формами. Большое число примеров и упражнений, последовательность которых тщательно продумана, значительно расширяет содержание руководства.

Предназначено для студентов первого курса всех факультетов.

2

Лекция 1

Пространство геометрических векторов

Линейные операции над геометрическими векторами. Коллинеарные и компланарные векторы. Базис, координаты вектора, их свойства. Проекция вектора на ось. Декартов базис и декартовы координаты вектора.

Декартовы координаты точки.

1.1. Понятие геометрического вектора.

Линейные операции над векторами, их свойства

Определение 1. Геометрическим вектором (или просто вектором) называется отрезок, концы которого рассматриваются в определенном порядке (т.е. указано, какая

из его граничных точек является началом, а какая – концом).

Если за начало отрезка AB принята точка A , вектор будем обозначать символом AB

(либо одной малой латинской буквой, например, a ), а точку A называть точкой приложения вектора.

На чертеже вектор AB будем изображать отрезком со стрелкой в конечной точке (рис.

1.1).

B

A

Рис. 1.1

Длиной вектора AB назовем длину отрезка AB и в записи используем знак абсолютной

величины: AB (либо a ).

Вектор AB называется нулевым вектором, если его конечная точка B совпадает с начальной A .

Нулевой вектор в силу его определения не имеет направления, а длина его равна

нулю.

направление и равные длины (рис. 1.4).

3

Равенства (1.4) и (1.5) дают следующее:

OC a b c .

Сравнив последнее равенство с (1.3), получим

a b c a b c ,

и свойство 2 доказано.

Замечание 2. Свойство 2 означает, что мы можем далее не различать векторы

a b c и a b c , а рассматривать их как один и тот же вектор a b c .

5

Рис. 1.9

вектора an 1 приложим вектор an , тогда вектор, начало которого

совпадет с началом a1 , а конец – с концом an , и будет вектором a1 ... an (рис. 1.9).

Замечание 3. Существует такой вектор , что для любого геометрического вектора

a справедливо равенство

a a a .

Действительно, в качестве вектора можно взять введенный ранее нулевой вектор.

Если a – произвольный геометрический вектор, то по определению суммы вектор

a имеет начало в начале a , а конец – в конце второго слагаемого, т. е. , но у начало и конец совпадают и, таким образом, у вектора a начало совпадает с началом вектора

1.2. Линейная зависимость векторов

Линейной комбинацией векторов a1,..., an с коэффициентами 1,..., n будем называть сумму

u 1a1 ... nan .

Определение 5. Векторы a1,..., an называются линейно зависимыми, если найдутся

такие числа 1,..., n , не все равные нулю одновременно, что

Рассмотрим линейную комбинацию 0 a1 ...1 ak ... 0 an , причем среди коэффициентов не все равны нулю ( k 1). Следовательно, в соответствии с определением 5 система a1,..., an линейно зависима.

Теорема 2. Всякая система векторов a1,..., an , содержащая линейно зависимую подсистему k векторов, 1 k n , линейно зависима.

Доказательство. Пусть для определенности линейно зависимы первые k векторов a1,..., ak (это допущение не ограничивает общности рассуждений, так как мы могли бы перенумеровать всю исходную систему, если бы были линейно зависимы другие векторы).

Это означает, что найдутся числа 1,..., k , не все равные нулю, и такие что

1 a1 ... k ak .

Но линейная комбинация всей системы n векторов a1,..., an с коэффициентами

1,..., k , 0,..., 0 равна :

n k нулей

8

1 a1 ... k ak 0 ak 1 ... 0 an .

Следовательно, система a1,..., an линейно зависима.

Теоремы 3 – 5 проясняют понятие линейной зависимости для геометрических

векторов.

Теорема 3. Необходимым и достаточным условием линейной зависимости двух

геометрических векторов является их коллинеарность.

Доказательство. Необходимость. Пусть a и b линейно зависимы. Тогда

существуют числа и (хотя бы одно из которых не равно нулю), что a b .

обозначим

равен произведению другого на число, следовательно (см. определение 4), векторы a и b

коллинеарны.

Обратно. Пусть векторы a и b коллинеарны.

Случай 1. Хотя бы один из векторов нулевой: a (либо b , либо a b ), тогда

(см. теорему 1) система a , b линейно зависима.

Случай 2. a , b . В силу замечания 5 найдется число такое, что b a ,

следовательно, a (1) b , и линейная комбинация векторов a и b с коэффициентами,

не равными нулю одновременно, равна нулевому вектору, – это означает, что система a , b линейно зависима.

Следствие. Если два вектора a и b не коллинеарны, они линейно независимы

(допустим противное, тогда a и b коллинеарны ему (см. теорему 3), что противоречит

условию).

Определение 7. Векторы называются компланарными, если они лежат в одной или параллельных плоскостях (рис. 1.13).

1 a 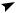b

c

2

Рис. 1.13

Теорема 4. Необходимым и достаточным условием линейной зависимости трех геометрических векторов является их компланарность.

Доказательство. Необходимость. Пусть векторы a , b и c линейно зависимы.

Тогда существуют такие числа , , , не все равные нулю, что выполняется равенство

9

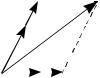
a b c .

Пусть для определенности 0 (это допущение не ограничивает общности

Случай 1. В системе векторов a , b , c присутствует нулевой вектор ,

следовательно (см. теорему 1), система a , b , c линейно зависима.

Случай 2. a , b , c и какая-нибудь пара из векторов a , b , c коллинеарна,

следовательно (см. теорему 3), эта пара составляет линейно зависимую подсистему в системе a , b , c , тогда вся система a , b , c линейно зависима (см. теорему 2).

что означает линейную зависимость системы a , b , c .

Следствие 1. Пусть a и b не коллинеарны, тогда любой вектор c плоскости можно

представить в виде их линейной комбинации (см. доказательство достаточности, случай

3).

10