2.За завданням викладача для кожного з досліджуваних тіл (куля, циліндр та ін.) провести по 5-9 дослідів. Визначити час скочування кожного тіла.

3.Виміряти довжину похилої площини і її висоту.

4.Зважити досліджувані тіла і зробити необхідні виміри їх геометричних розмірів. Дані усіх вимірів занести в табл.2.3.1.

Обробка результатів експерименту

1.За формулою (2.3.11) обчислити момент інерції досліджуваних тіл за результатами експерименту.

2.За формулами (1.45 – 1.52) для відповідних тіл обчислити теоретичне значення їх моментів інерції.

3.Порівняти результати теоретичних обчислень та зіставити їх із результатами експерименту. Зробити висновки.

4.Обчислити абсолютну і відносну похибки експерименту.

Контрольні питання

1.Момент інерції твердого тіла. Кінетична енергія поступального та обертового рухів твердого тіла. Закон збереження енергії в механіці. Консервативні та дисипативні сили (с. 18 -21, 9-11).

2.Обчислення моментів інерції деяких тіл (однорідний стержень, диск, диск із центральним отвором, обруч, куля). Теорема Штейнера (с. 18-21, 23).

3.Експериментальні методи визначення моментів інерції твердих тіл (с. 35-38).

4.Вивести робочу формулу для визначення моменту інерції тіла при допомозі похилої площини (с. 35-37).

5.Момент сили. Рівняння моментів. Момент імпульсу. Закон збереження моменту імпульсу. Гіроскопи. Основне рівняння динаміки обертового руху (с.16-18, 23-24) .

39

40

41

Лабораторна робота 1.4 Визначення моменту інерції маховика

Мета роботи. Вивчення закону збереження механічної енергії шляхом визначення моменту інерції маховика.

Прилади і матеріали. 1. Маховик. 2. Секундомір. 3. Терези.4. Лінійка з міліметровими поділками. 5. Тягарець. 6. Штангенциркуль.

Теоретичні відомості та опис лабораторної установки

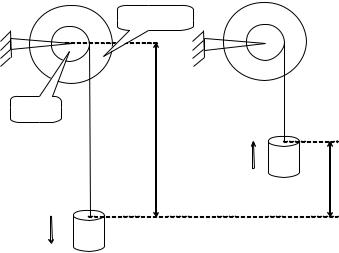
Установка для визначення моменту інерції маховика складається з маховика та шківа , які насаджені на вал (рис. 2.4.1). Вал закріплений у двох підшипниках. На шків намотують нитку і до кінця її прикріплюють тягар масою m. Падаючи, тягар надає рівноприскореного обертання шківу, а через нього – валу й маховику.

Маховик

Шків

h

V m

h1

V m

Рис. 2.4.1

Потенціальна енергія тягаря при цьому перетворюється в кінетичну енергію поступального руху тягаря, кінетичну енергію

42

обертального руху маховика і витрачається на перемагання сил тертя (кінетичною енергією обертального руху шківа з валом нехтуємо, адже вона мала порівняно з попередніми складовими).

Кінетична енергія поступального руху тягаря та кінетична енергія обертального руху маховика визначаються за формулами:

Робота, що затрачається на перемагання сил тертя, при одному оберті маховика нехай складає А, а робота за кілька обертів AЧn1

(де п1 – кількість обертів маховика, які він зробив під дією тягаря).

Отже, для даної системи можна застосувати закон збереження механічної енергії, враховуючи при цьому втрати механічної енергії на роботу проти сил тертя:

Момент інерції маховика можна визначити за допомогою описаної установки двома методами.

І метод. Нитка не прикріплена до шківа. У момент, коли тягар повністю опустився, нитка спадає і шків, продовжуючи обертатись, робить n2 обертів, поки повністю не зупиниться. За цей час за рахунок кінетичної енергії обертального руху маховика, яку він мав у момент спадання нитки, виконується робота, спрямована на перемагання сили тертя, що дорівнює:

звідки

43

Виразимо лінійнуV і кутову ω швидкості через вимірювані в досліді величини – висоту падіння тягаря h і час його падіння t:

де r – радіус шківа.

Замінивши V і ω у (2.4. 6) через їх значення (2.4.7) і (2.4.8), знайдемо:

ІІ метод. Нитка прикріплена одним кінцем до шківа. Коли тягар повністю опуститься, маховик, продовжуючи обертатись за інерцією, підніме тягар на висоту h1 < h. При цьому система набуде потенціальної енергії

Із (2.4.11) маємо:

44