
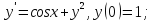


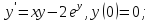



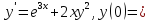 1;
1;
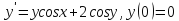 ;
;



 1;
1;


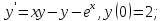
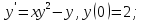

















 0;
0;
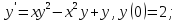
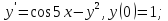







 2;
2;
































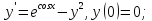
















100.

Розкласти задану графічно функцію f(t) в тригонометричний ряд Фур’є,вважаючи що: а)зображена на графіку функція періодична і задана на своєму повному періоді; б) зображена на графіку функція задана на півперіоді,і продовжуючи її в номерах варіантів з парними номерами парним чином,а в номерах варіантів з непарними номерами - непарним чином,отримати відповідний розклад в ряд Фур’є в укороченій формі.
f(t)
1)
2
1 t
f(t)
2)
3
3 t
f(t)
3)
2 t
-2
f(t)
4)
2
3 t
f(t)
5)
1
-1 t
6) f(t)
-2 1 t
7) f(t)
1
1 t
8) f(t)
-2 t
-2
f(t)
9)
2
-4 t
10) f(t)
3 t
-1
11) f(t)
4
3 t
f(t)
12)
3
-2 t
13) f(t)
4 t
-2
14) f(t)
2
-2 t
f(t)
15)
3
2 3 t
16) f(t)
-3 t
-1
17) f(t)
-2 t
-2
18) f(t)
3
-1 t
f(t)
19) 4
1 t
f(t)
20)
-4 t
-3
21) 5 f(t)
1 t
22) f(t)
-4 1 t
23) f(t)
2 t
-3
24) f(t)
3
-4 t
25) f(t)
-4 t
-3
26) f(t)
3
4 t
27) f(t)
-3 t
-2
f(t)
28) 3
-1 t
29) f(t)
4 t
-1
30) f(t)
3
-5 t
31) f(t)
3 t
-2
32) f(t)
-2 t
-2
33) f(t)
3 t
-3
34) f(t)
3
-2 t
f(t)
4
35)
1 t
36) f(t)
3
-2 t
37) f(t)
4 t
-1
38) f(t)
-2 t
-1
39) f(t)
1
-6 t
40) f(t)
-4 t
-2
41) f(t)
3
3 t
-1
42) f(t)
2
3 t
43) f(t)
3 t
-2
f(t)
44)
2
-5 t
45) f(t)
-5 t
-1
46) f(t)
3
-4 t
47) f(t)
-1 t
-3
f(t)
48) 4
-2 t
49) f(t)
1
4 t
50) f(t)
-4 t
-2
f(t)
51) 4
1 t
52) f(t)
1
-5 t
53) f(t)
1 2 t
f(t)
54) 4
1 t
55) f(t)
1
5 t
56) f(t)
-2 t
-3
57) f(t)
4
-3 t
58) f(t)
3
-5 t
59) f(t)
3
4 t
f(t)
60) 5
-2 t
61) f(t)
4 t
-2
62) f(t)
2
4 t
63) f(t)
-2 t
-3
64) f(t)
6 t
-1
65) f(t)
4 t
-1
f(t)
66)
4
-3 t
67) f(t)
-6 1 t
f(t)
68) 3
-3 t
f(t)
69)
5
4 t
70) f(t)
2
-3 t
71) f(t)
2
3 t
72) f(t)
-4 t
-2
73) f(t)
3
2 t
74) f(t)
-5 t
-2
75) f(t)
3 t
-2
76) f(t)
4
-5 t
77) f(t)
2
5 t
78) f(t)
4 t
-1
79) f(t)
-6 t
-3
80) f(t)
4
-5 t
81) f(t)
-1 t
-4
82) f(t)
-7 1 t
83) f(t)
2
5 t
f(t)
84) 3
-5 t
85) f(t)
1 t
-3
86) f(t)
7 t
-2
87) f(t)
-5 t
-1
88) f(t)
5 t
-1
89) f(t)
-4 t
-1
90) f(t)
1
-4 t
91) f(t)
2
-3 t
92) f(t)
3 t
-1
93) f(t)
4
-4 t
94) f(t)
3
-4 t
95) f(t)
4
2 t
96) f(t)
-4 t
-1
97) f(t)
1 t
-3
f(t)
98)
2
-5 t
99) f(t)
5 t
-3
f(t)
100)
2
5 t
Контрольні питання теоретичного та практичного змісту в тестовій формі
1. Означений інтеграл дорівнює

а)
 ;
б)
;
б)
 ;
в)
;
в) ;
г)
;
г)
 .
.2. Означений інтеграл дорівнює

а)
 ;
б)
;
б)
 ;
в)
4;
г)
;
в)
4;
г)
 .
.3 . Означений інтеграл дорівнює

а) 10; б) 20; в) 30; г) 40.
4. Означений інтеграл дорівнює

а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г) 5.
;
г) 5.5. Означений інтеграл дорівнює

а)
 ;
б)
;
б) ;
в)
;
в) ;
г) 3.
;
г) 3.6. Означений інтеграл дорівнює

а) 3; б) 6; в) 9; г) -5.
7. Означений інтеграл дорівнює

а) 1; б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.8. Означений інтеграл дорівнює


а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)
 .
.9.Лінійним диференціальним рівнянням першого порядку є:
 ;
;
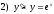 ;
; ;
; .
.10.Загальним розв’язком диференціального рівняння
 є:
є: ;
;
 ;
; ;
;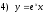 .
.11.Корені характеристичного рівняння

 Тоді загальний розв’язок диференціального
рівняння
Тоді загальний розв’язок диференціального
рівняння має вигляд
має вигляд ;
;
 ;
; ;
; .
.12.Загальний розв’язок диференціального рівняння
 є
є .
.Частинний розв’язок ДР, що задовольняє початкову умову
 ,
має вигляд:
,
має вигляд: ;
;
 ;
; ;
; .
.13. Характеристичне рівняння для диференціального рівняння
 має вигляд:
має вигляд: ;
; ;
; ;
; .
.14.Рівнянням з відокремлюваними змінними є:
 ;
;
 ;
; ;
; .
.15. Загальним розв’язком диференціального рівняння
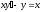 є:
є: ;
;
 ;
; ;
; .
.16.Загальним розв’язком диференціального рівняння
 є:
є: ;
;
 ;
; ;
; .
.17.Характеристичне рівняння для диференціального рівняння
 має вигляд:
має вигляд: ;
; ;
; ;
; .
.18. Рівнянням з відокремлюваними змінними є:
 ;
;
 ;
; ;
;19. Корені характеристичного рівняння

 Тоді
Тодізагальний розв’язок диференціального рівняння
 має вигляд:
має вигляд: ;
;
 ;
; ;
; .
.20. Загальним розв’язком диференціального рівняння
 є:
є: ;
;
 ;
; ;
; .
.21. Загальним розв’язком диференціального рівняння
 є:
є: ;
;
 ;
; ;
; .
.22.Загальний розв’язок диференціального рівняння

 .
Частинний
.
Частиннийрозв’язок ДР, що задовольняє початкову умову
 ,
має вигляд:
,
має вигляд: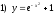 ;
;
 ;
; ;
; .
.23.Корені характеристичного рівняння

 Тоді загальний
Тоді загальнийрозв’язок диференціального рівняння
 має вигляд
має вигляд ;
;
 ;
; ;
; .
.24.Загальний інтеграл диференціального рівняння
 дорівнює
дорівнює .
Частинний розв’язок ДР, що задовольняє
початкову умову
.
Частинний розв’язок ДР, що задовольняє
початкову умову
 ,
,має вигляд:
 ;
;
 ;
; ;
; .
.25.Інтервал збіжності ряду
 має вигляд
має вигляд .
При
.
При отриманий
отриманийчисловий ряд збіжний, а при
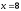 розбіжний. Тоді областю збіжності
даного ряду є:
розбіжний. Тоді областю збіжності
даного ряду є:а)
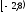 ;
б)
;
б) ; в)
; в) ; г)
; г) .
.26. Який з перерахованих рядів є рядом Маклорена?
а)
 ;
б)
;
б) ;
в)
;
в) ;
;г)
 .
.27. Ряд
 є:
є:1. а) збіжним; б) розбіжним; в) абсолютно збіжним; г) умовно збіжним.
28. Ряд
 є:
є:а) збіжним; б) розбіжним; в) абсолютно збіжним; г) умовно збіжним.
29. Чому дорівнює коефіцієнт
 ряду Фур'є
ряду Фур'є
 ?
?а)
 ; б)
; б) ;
;в)
 ;
г)
;
г)
 .
.30. Розклад в степеневий ряд Маклорена функції
 має
вигляд:
має
вигляд:а)
 б)
б)

в)
 г)
г)
 .
.31. Дослідивши за радикальною ознакою Коші ряд
 ,
можна зробити висновок,
,
можна зробити висновок,що він є:
а) збіжним; б) розбіжним; в) абсолютно збіжним; г) умовно збіжним.
32. Розклад в степеневий ряд Маклорена функції
 має
вигляд:
має
вигляд:а)
 б)
б)

в)
 г)
г)
 .
.33. Який з наведених рядів є знакозмінним рядом?
а)
 ; б)
; б) ;
в)
;
в) ;
г)
;
г) .
.34.При яких значеннях
 узагальнений гармонічний
ряд (ряд Діріхлє)
узагальнений гармонічний
ряд (ряд Діріхлє)
 буде
будерозбіжним?
а)
 ;
б)
;
б) ;
в)
;
в) ;
г)
;
г)
 .
.35. Ряд
 є:
є:а) знакозмінним; б) степеневим ; в) гармонічним; г) знакододатнім.
36. Розклад в степеневий ряд Маклорена функції
 має
вигляд:
має
вигляд:а)
 б)
б)

в)
 г)
г)
 .
.37. Дослідивши за радикальною ознакою Коші ряд
 ,
можна зробити висновок,
,
можна зробити висновок,що він є:
а) збіжним; б) розбіжним; в) абсолютно збіжним; г) умовно збіжним.
38. Розклад в степеневий ряд Маклорена функції
 має
вигляд:
має
вигляд:а)
 б)
б)

в)
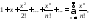 г)
г)

39. Щоб дослідити ряд
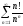 на збіжність, застосовуючи ознаку
Даламбера, необхідно
на збіжність, застосовуючи ознаку
Даламбера, необхіднознайти:
а)
 ;
б)
;
б)
 ;
в)
;
в)
 ;
г)
;
г)

40. Якщо радіус збіжності ряду
 дорівнює нулю(
дорівнює нулю( ),
то ряд збіжний:
),
то ряд збіжний:а) при
 ; б) при
; б) при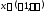 ;
в) при
;
в) при ;
;г) при
 .
.41. Дослідивши за ознакою Даламбера ряд
 ,
можна зробити висновок, що він є:
,
можна зробити висновок, що він є:а) збіжним; б) розбіжним; в) абсолютно збіжним; г) умовно збіжним.
Література
Луценко Ю.Л.,Канівець В.В.: навч.-метод. посіб. для студ.-заочн. Контрольні завдання, Вища математика. - Вінниця: ВДАУ, 2000. - С. 499.
Валєєв К.Г.,Джаладова І.А.,Яременко В.В.,Сліпушко О.М.: навч. посібник у 2 ч., Вища математика. - К.: , 2001. - С. 546.
Луценко Ю.Л., Чубатюк В.М. : Курс лекцій. Навчальний посібник для студентів агр, Прикладна математика. - Вінниця: ВДАУ, 2001. - С. 264.
Бугров Я.С.,Никольский С.М. : учеб. для студ. вузов, Высшая математика. Дифференциальное и интегральное исчисление. - М.: Наука, 1980. - С. 432.
Данко П.Е.,Попов А.Г.,Кожевникова Т.Я. : учеб. пособие для студ. втузов, Высшая математика в упражнениях и задачах: в 2. ч. Ч. 1. - М.: Высшая школа, 1986. - С. 304.
Барковський В..В.,Барковська Н.В. : Вища математика для економістів. - К.: Центр навчальної літератури, 2005. - С. 448.
Шкіль М.І., Колесник Т.В., Котлова В.М. : навч. посіб. для студ. вузів, Вища математика. Елементи аналітичної геометрії. Диференціальне та інтегральне числення функції однієї змінної. - К.: Вища школа, 1984. - С. 391.
Бугров Я.С., Никольский С.М. : , Высшая математика. Задачник. - М.: Наука, 1987. - С. 256.
Коваленко І.П. : Навчальний посібник, Вища математика. - К.: Вища школа, 2006. - С. 624.
Дубчак В.М.,Левчук О.В.:Методичні вказівки для проведення практичних занять, Вища математика. Практикум. - Вінниця: , 2004. - С.67.
Зайцев И.А. : учебник, Высшая математика. - М.: Высшая школа, 1991. - С. 400.
Шипачев В.С., Тихонов А.Н. : учеб. для вузов, Высшая математика. - М.: Высшая школа, 1990. - С. 479.
Васильченко І.П. : підручник, Вища математика для економістів. - К.: Знання, 2007. - С. 454.
Барковський В.В.,Барковська Н.В. : навч. посіб. для вузів, Вища математика для економістів. - К.: ЦУЛ, 2002. - С. 2002.
Барковський В. В., Барковська Н. В. : навч. посібник, Вища математика для економістів. - К.: Центр учбової літератури, 2010. - С. 417.
Клепко В.Ю., Голець В.Л. : навч. посібник. Вища математика в прикладах і задачах. - К.: ЦУЛ, 2009. - С. 592.
Дубчак В.М. Методичне забезпечення самостійної роботи студентів з вищої математики.Частина 1. навч.посібник. - Вінниця: , 2011. - С.162.
