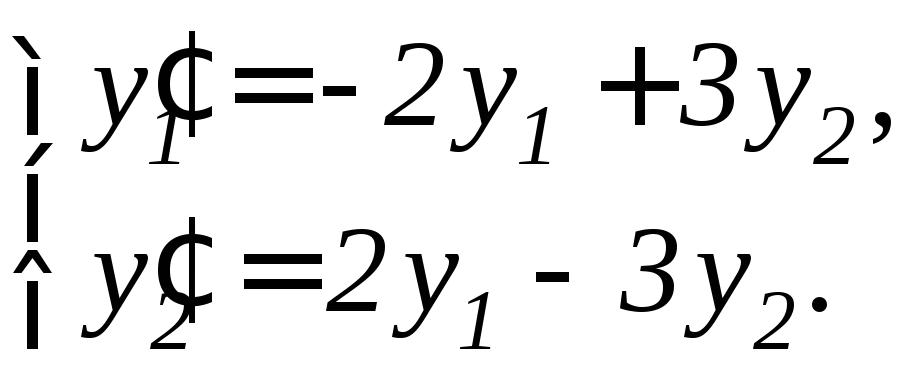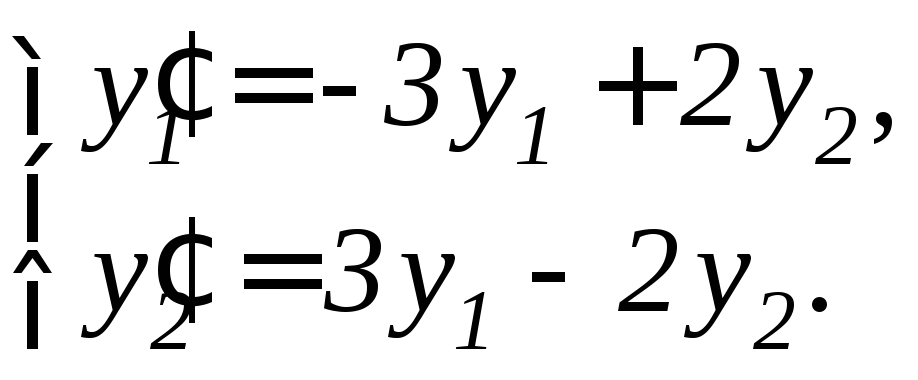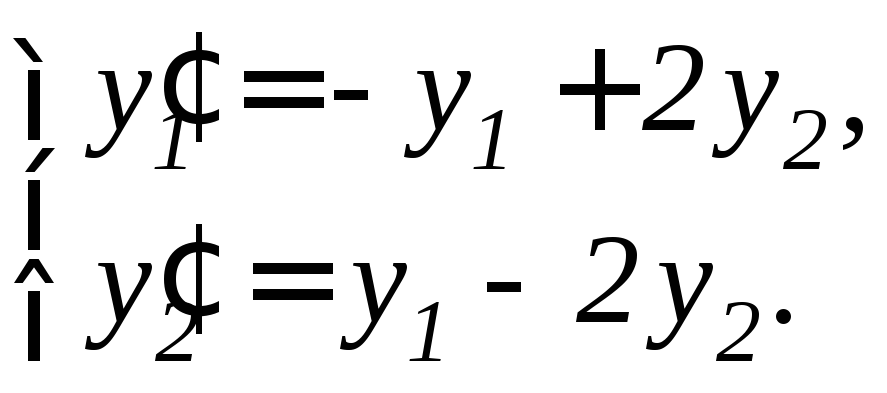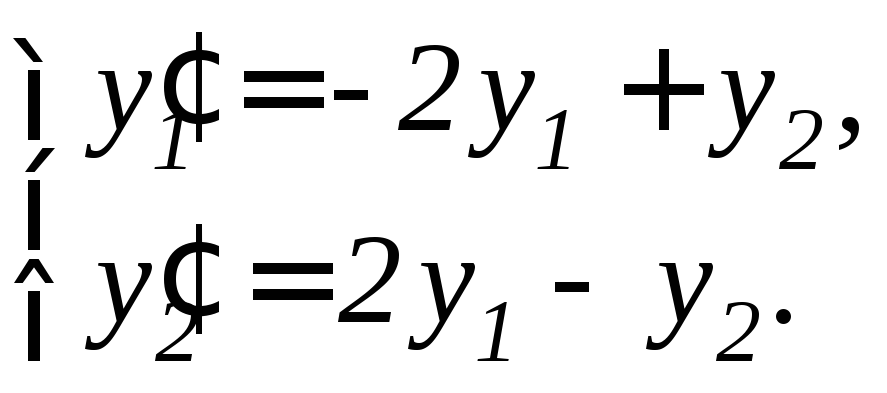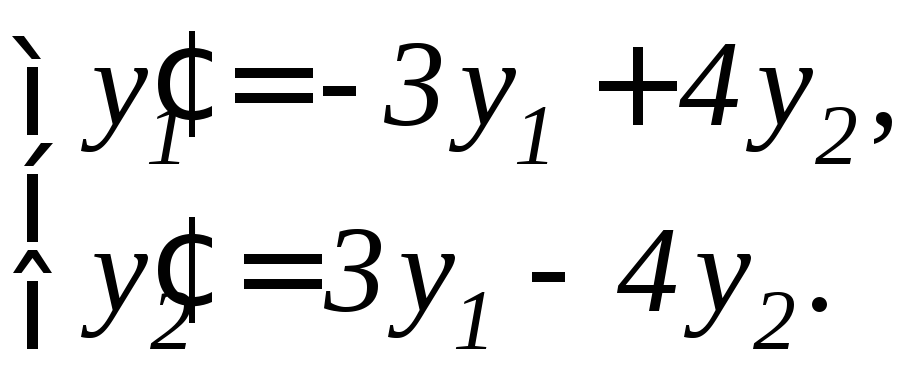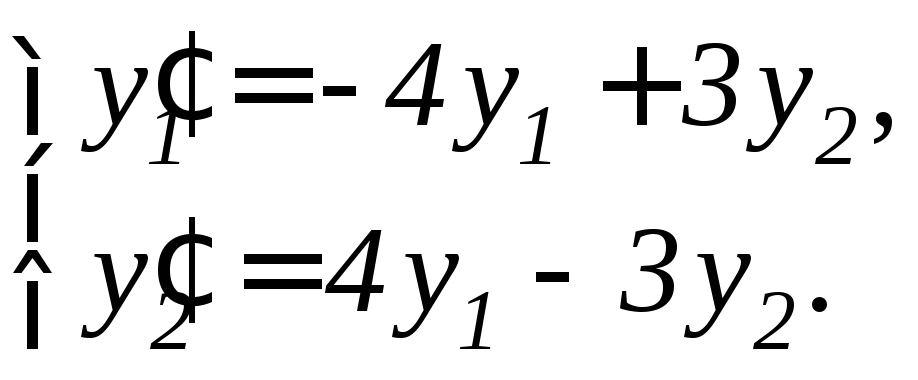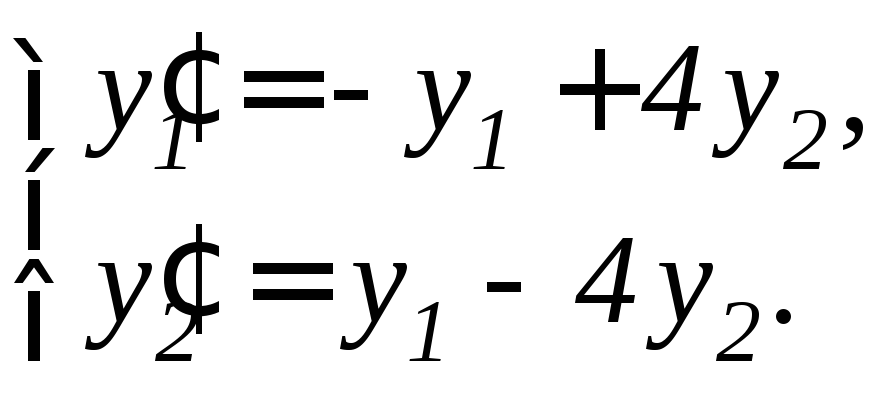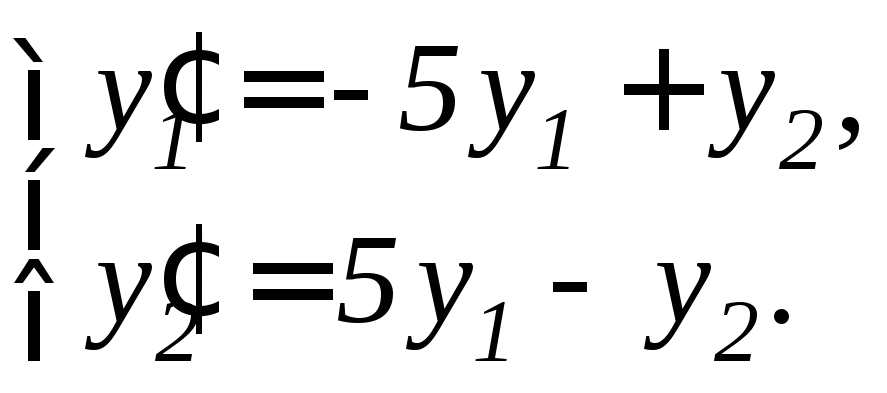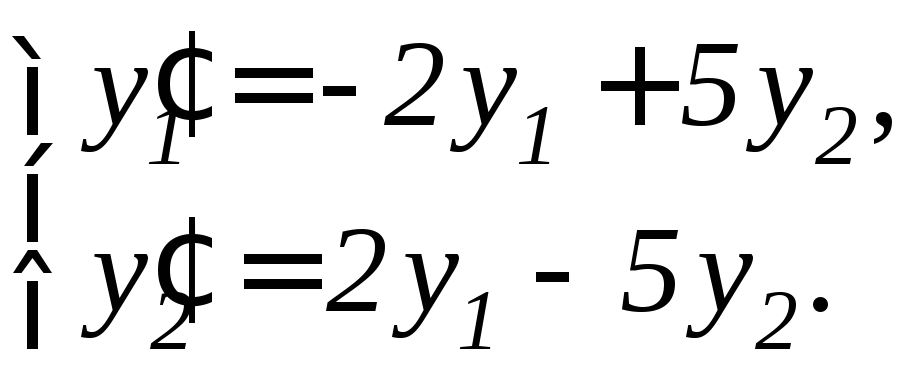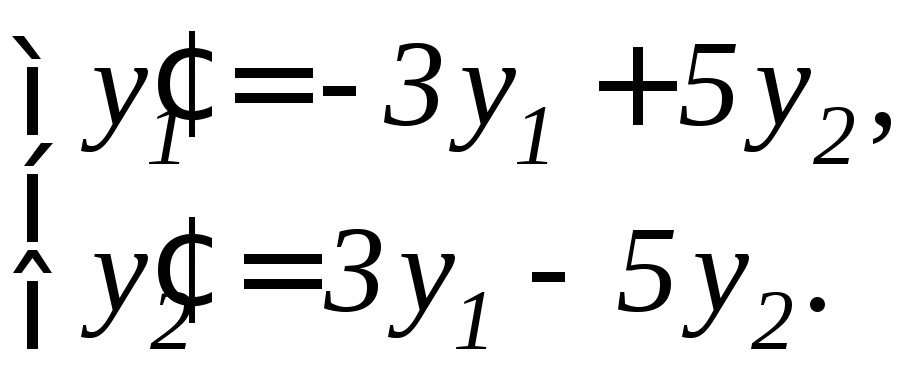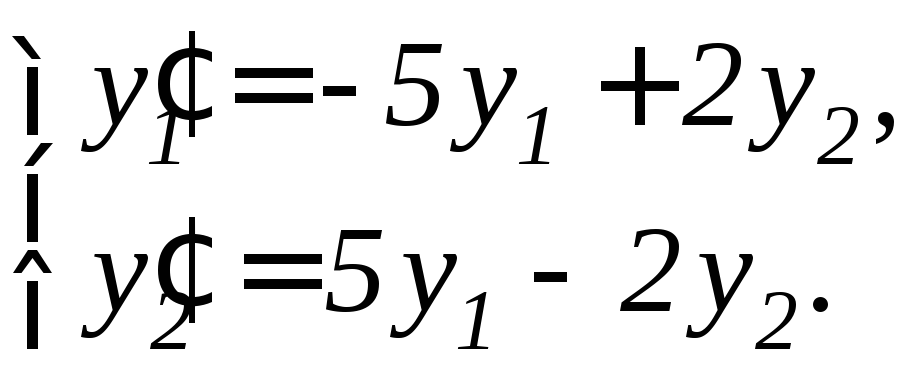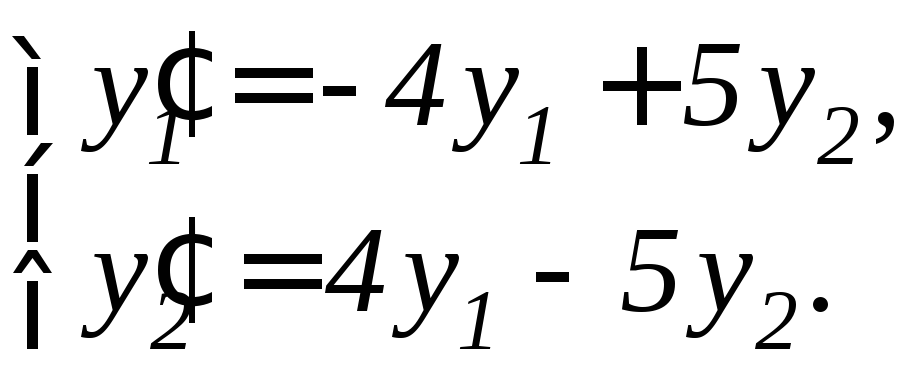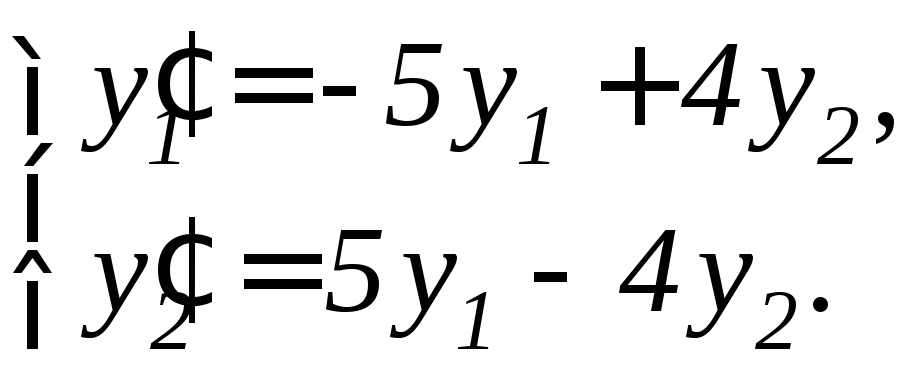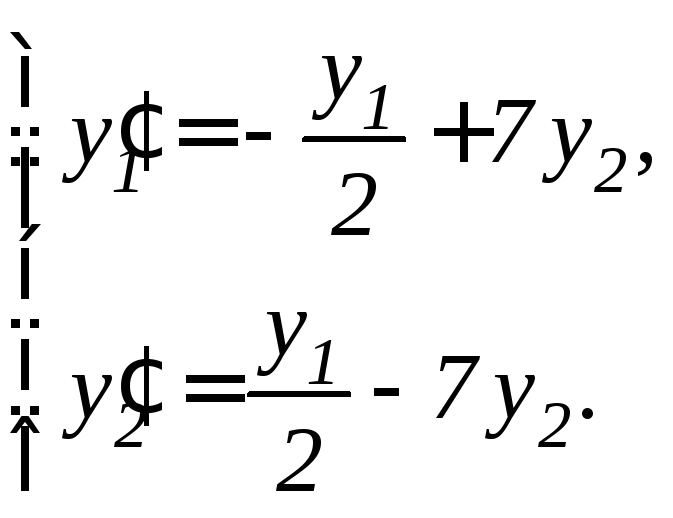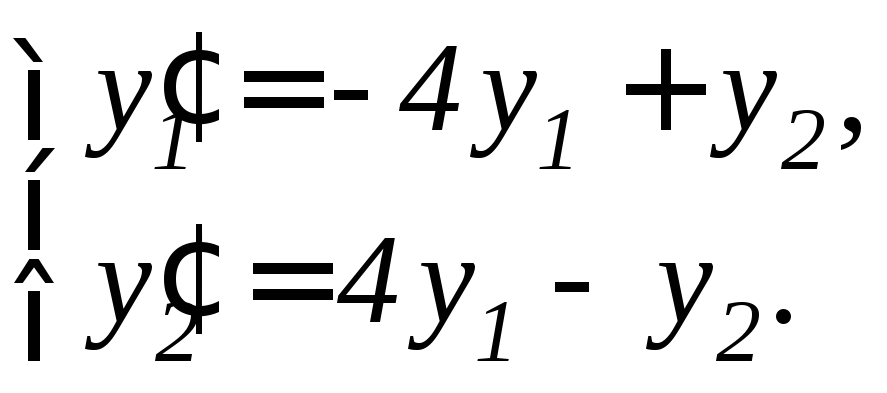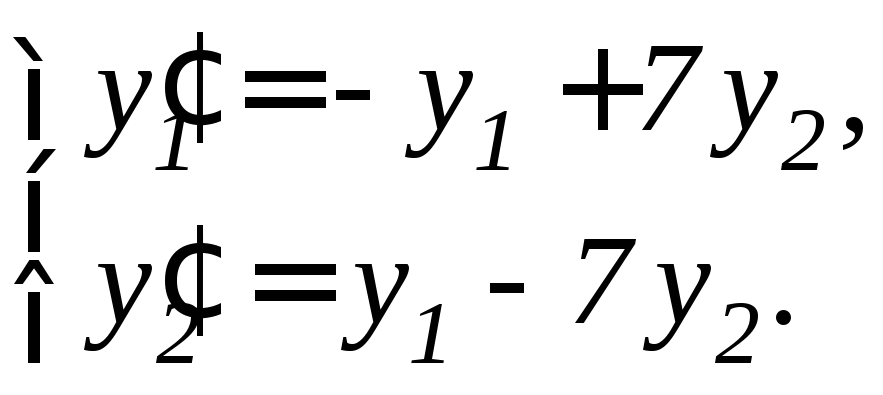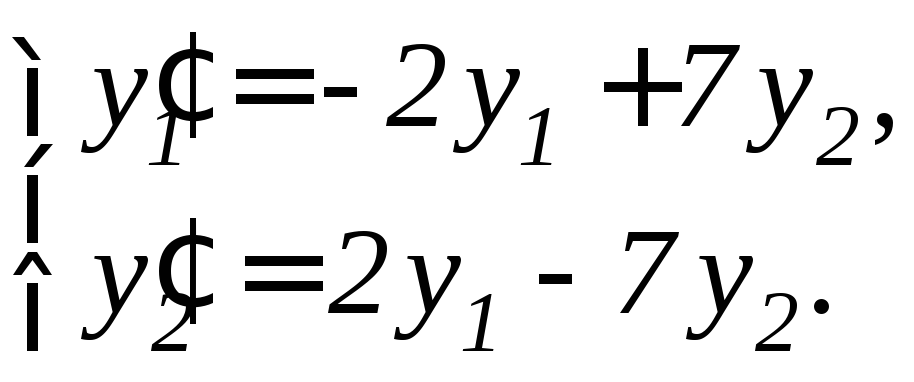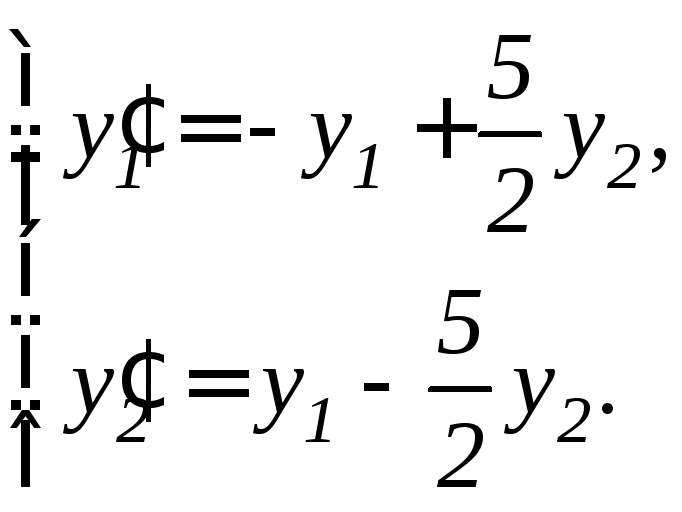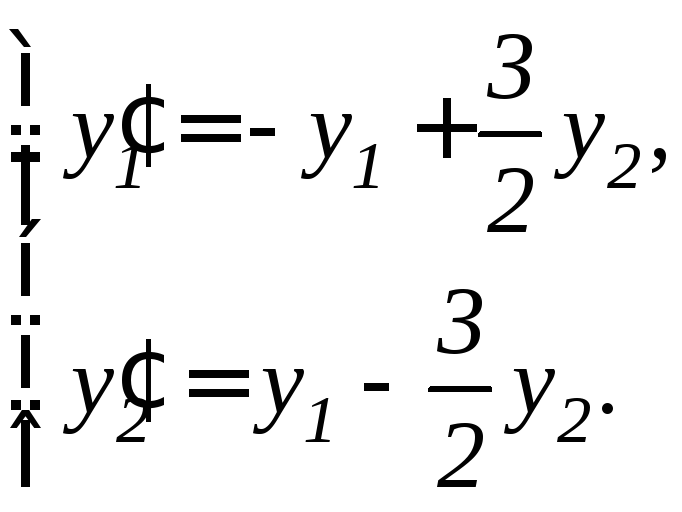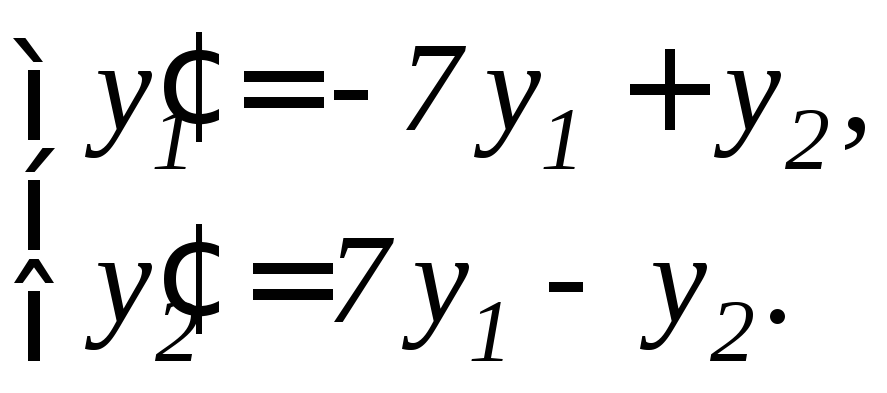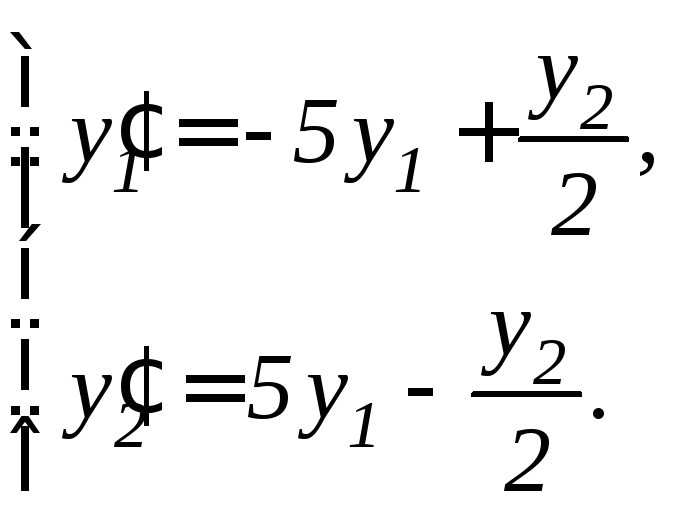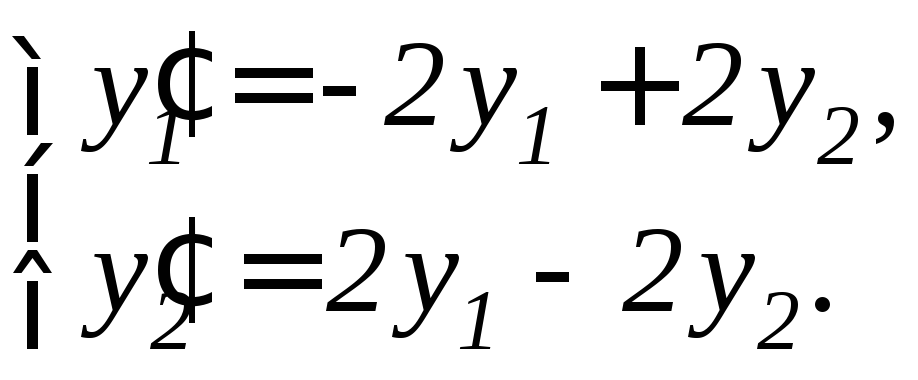11.5. Задачи
Доказать, что
функция
удовлетворяет дифференциальному
уравнению
:
|
1. |
|
2. |
|
|
3. |
|
4. |
|
|
5. |
| ||
|
6. |
| ||
,
.
,
.
,
.
,
.
,
.
,
.
7. Выяснить, являются
ли решениями дифференциального уравнения
следующие соотношения:
1)
;
2)
.
8. Зная общее решение
дифференциального уравнения
,
найти и построить его интегральные
кривые, проходящие через точки
,
,
.
Составить дифференциальные уравнения семейства линий:
|
9. |
|
10. |
|
11. |
|
|
12. |
|
13. |
|
14. |
|
|
15. |
|
16. |
|
17. |
|
.
.
.
.
.
.
.
.
.
Решить уравнения с разделяющимися переменными:
|
18. |
|
19. |
|
|
20. |
|
21. |
|
|
22. |
|
23. |
|
|
24. |
|
25. |
|
.
.
.
.
.
.
.
.Решить задачу Коши для уравнений с разделяющимися переменными:
|
26. |
|
27. |
|
|
28. |
|
29. |
|
|
30. |
|
31. |
|
|
32. |
|
33. |
|
,
.
,
.
,
.
,
.
,
.
,
.
,
.
,
.Решить однородные дифференциальные уравнения:
|
34. |
|
35. |
|
|
36. |
|
37. |
|
|
38. |
|
39. |
|
|
40. |
|
41. |
|
.
.
.
.
.
.
.
.Решить задачу Коши для однородных дифференциальных уравнений:
|
42. |
|
|
|
|
43. |
| ||
|
44. |
| ||
,
.
,
.
,
.Решить линейные уравнения:
|
45. |
|
46. |
|
|
47. |
|
48. |
|
|
49. |
|
50. |
|
.
.
,
.
.
,
.
.Решить уравнения Бернулли:
|
51. |
|
52. |
|
|
53. |
|
54. |
|
.
.
,
.
.Решить уравнения в полных дифференциалах:
|
55. |
|
56. |
|
|
57. |
|
| |
|
58. |
|
| |
.
.
.
.
Решить уравнения,
имеющие интегрирующий множитель,
зависящий только от
или только от
:
|
59. |
|
60. |
|
.
.Решить дифференциальные уравнения, допускающие понижение порядка:
|
61. |
|
62. |
|
|
63. |
|
64. |
|
|
65. |
|
66. |
|
|
67. |
|
68. |
|
|
69. |
|
70. |
|
.
.
.
.
.
.
.
.
,
,
.
.
Решить линейные однородные уравнения с постоянными коэффициентами:
|
71. |
|
72. |
|
73. |
|
|
74. |
|
75. |
|
76. |
|
|
77. |
|
78. |
|
79. |
|
|
80. |
|
81. |
|
82. |
|
.
.
.
.
.
.
.
.
.
.
.
.Решить неоднородные уравнения:
|
83. |
|
84. |
|
|
85. |
|
86. |
|
|
87. |
|
88. |
|
|
89. |
|
90. |
|
|
91. |
|
92. |
|
.
.
.
.
.
.
.
.
.
,
,
.
Методом исключения неизвестных решить системы уравнений:
|
93. |
|
94. |
|
Решить системы дифференциальных уравнений с постоянными коэффициентами:
|
95. |
|
96. |
|
97. |
|
|
98. |
|
99. |
|
|
|
|
100. |
|
|
| ||
Методом вариации постоянных решить неоднородные системы уравнений:
|
101. |
|
102. |
|
Задание 11.1. Найти решение дифференциального уравнения:
|
1. |
а) |
|
|
б) |
|
|
2. |
а) |
|
|
б) |
|
|
3. |
а) |
|
|
б) |
|
|
4. |
а) |
|
|
б) |
|
|
5. |
а) |
|
|
б) |
|
|
6. |
а) |
|
|
б) |
|
|
7. |
а) |
|
|
б) |
|
|
8. |
а) |
|
|
б) |
|
|
9. |
а) |
|
|
б) |
|
|
10. |
а) |
|
|
б) |
|
|
11. |
а) |
|
|
б) |
|
|
12. |
а) |
|
|
б) |
|
|
13. |
а) |
|
|
б) |
|
|
14. |
а) |
|
|
б) |
|
|
15. |
а) |
|
|
б) |
|
|
16. |
а) |
|
|
б) |
|
|
17. |
а) |
|
|
б) |
|
|
18. |
а) |
|
|
б) |
|
|
19. |
а) |
|
|
б) |
|
|
20. |
а) |
|
|
б) |
|
|
21. |
а) |
|
|
б) |
|
|
22. |
а) |
|
|
б) |
|
|
23. |
а) |
|
|
б) |
|
|
24. |
а) |
|
|
б) |
|
|
25 |
а) |
|
|
б) |
|
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
Задание 11.2. Найти общее решение дифференциального уравнения:
|
1. |
а) |
|
|
б) |
|
|
2. |
а) |
|
|
б) |
|
|
3. |
а) |
|
|
б) |
|
|
4. |
а) |
|
|
б) |
|
|
5. |
а) |
|
|
б) |
|
|
6. |
а) |
|
|
б) |
|
|
7. |
а) |
|
|
б) |
|
|
8. |
а) |
|
|
б) |
|
|
9. |
а) |
|
|
б) |
|
|
10. |
а) |
|
|
б) |
|
|
11. |
а) |
|
|
б) |
|
|
12. |
а) |
|
|
б) |
|
|
13. |
а) |
|
|
б) |
|
|
14. |
а) |
|
|
б) |
|
|
15. |
а) |
|
|
б) |
|
|
16. |
а) |
|
|
б) |
|
|
17. |
а) |
|
|
б) |
|
|
18. |
а) |
|
|
б) |
|
|
19. |
а) |
|
|
б) |
|
|
20. |
а) |
|
|
б) |
|
|
21. |
а) |
|
|
б) |
|
|
22. |
а) |
|
|
б) |
|
|
23. |
а) |
|
|
б) |
|
|
24. |
а) |
|
|
б) |
|
|
25. |
а) |
|
|
б) |
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задание 11.3. Найти решение дифференциального уравнения:
|
1. |
а) |
|
|
б) |
|
|
2. |
а) |
|
|
б) |
|
|
3. |
а) |
|
|
б) |
|
|
4. |
а) |
|
|
б) |
|
|
5. |
а) |
|
|
б) |
|
|
6. |
а) |
|
|
б) |
|
|
7. |
а) |
|
|
б) |
|
|
8. |
а) |
|
|
б) |
|
|
9. |
а) |
|
|
б) |
|
|
10. |
а) |
|
|
б) |
|
|
11. |
а) |
|
|
б) |
|
|
12. |
а) |
|
|
б) |
|
|
13. |
а) |
|
|
б) |
|
|
14. |
а) |
|
|
б) |
|
|
15. |
а) |
|
|
б) |
|
|
16. |
а) |
|
|
б) |
|
|
17. |
а) |
|
|
б) |
|
|
18. |
а) |
|
|
б) |
|
|
19. |
а) |
|
|
б) |
|
|
20. |
а) |
|
|
б) |
|
|
21. |
а) |
|
|
б) |
|
|
22. |
а) |
|
|
б) |
|
|
23. |
а) |
|
|
б) |
|
|
24. |
а) |
|
|
б) |
|
|
25. |
а) |
|
|
б) |
|
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
,
.
.
Задание 11.4. Найти общее решение дифференциального уравнения:
|
1. |
|
|
2. |
|
|
3. |
|
|
4. |
|
|
5. |
|
|
6. |
|
|
7. |
|
|
8. |
|
|
9. |
|
|
10. |
|
|
11. |
|
|
12. |
|
|
13. |
|
|
14. |
|
|
15. |
|
|
16. |
|
|
17. |
|
|
18. |
|
|
19. |
|
|
20. |
|
|
21. |
|
|
22. |
|
|
23. |
|
|
24. |
|
|
25. |
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задание 11.5. Найти общее решение дифференциального уравнения:
|
1. |
а) |
|
б) |
|
в) |
|
|
2. |
а) |
|
б) |
|
в) |
|
|
3. |
а) |
|
б) |
|
в) |
|
|
4. |
а) |
|
б) |
|
в) |
|
|
5. |
а) |
|
б) |
|
в) |
|
|
6. |
а) |
|
б) |
|
в) |
|
|
7. |
а) |
|
б) |
|
в) |
|
|
8. |
а) |
|
б) |
|
в) |
|
|
9. |
а) |
|
б) |
|
в) |
|
|
10. |
а) |
|
б) |
|
в) |
|
|
11. |
а) |
|
б) |
|
в) |
|
|
12. |
а) |
|
б) |
|
в) |
|
|
13. |
а) |
|
б) |
|
в) |
|
|
14. |
а) |
|
б) |
|
в) |
|
|
15. |
а) |
|
б) |
|
|
|
|
|
в) |
| ||||
|
16. |
а) |
|
б) |
|
в) |
|
|
17. |
а) |
|
б) |
|
в) |
|
|
18. |
а) |
|
б) |
|
в) |
|
|
19. |
а) |
|
б) |
|
в) |
|
|
20. |
а) |
|
б) |
|
в) |
|
|
21. |
а) |
|
б) |
|
в) |
|
|
22. |
а) |
|
б) |
|
в) |
|
|
23. |
а) |
|
б) |
|
в) |
|
|
24. |
а) |
|
б) |
|
в) |
|
|
25. |
а) |
|
б) |
|
в) |
|
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
Задание 11.6. Найти решение дифференциального уравнения:
|
1. |
а) |
|
б) |
|
|
2. |
а) |
|
б) |
|
|
3. |
а) |
|
б) |
|
|
4. |
а) |
|
б) |
|
|
5. |
а) |
|
б) |
|
|
6. |
а) |
|
б) |
|
|
7. |
а) |
|
б) |
|
|
8. |
а) |
|
|
|
|
|
б) |
| ||
|
9. |
а) |
|
|
|
|
|
б) |
| ||
|
10. |
а) |
|
|
|
|
|
б) |
| ||
|
11. |
а) |
|
б) |
|
|
12. |
а) |
|
б) |
|
|
13. |
а) |
|
б) |
|
|
14. |
а) |
|
б) |
|
|
15. |
а) |
|
б) |
|
|
16. |
а) |
|
|
|
|
|
б) |
| ||
|
17. |
а) |
|
б) |
|
|
18. |
а) |
|
б) |
|
|
19. |
а) |
|
б) |
|
|
20. |
а) |
|
б) |
|
|
21. |
а) |
|
б) |
|
|
22. |
а) |
|
|
|
|
|
б) |
| ||
|
23. |
а) |
|
б) |
|
|
24. |
а) |
|
б) |
|
|
25. |
а) |
|
б) |
|
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
.
,
,
.
,
,
.
.
,
,
.
.
,
,
.
Задание 11.7. Решить систему дифференциальных уравнений а) методом исключения неизвестных, б) методом Эйлера:
|
1. |
|
2. |
|
3. |
|
|
4. |
|
5. |
|
6. |
|
|
7. |
|
8. |
|
9. |
|
|
10. |
|
11. |
|
12. |
|
|
13. |
|
14. |
|
15. |
|
|
16. |
|
17. |
|
18. |
|
|
19. |
|
20. |
|
21. |
|
|
22. |
|
23. |
|
24. |
|
|
25. |
|
|
|
|
|
Интервал может быть как конечным, так и бесконечным в одну или обе стороны.
Решение дифференциального уравнения, выраженное в неявной форме, называют интегралом этого уравнения
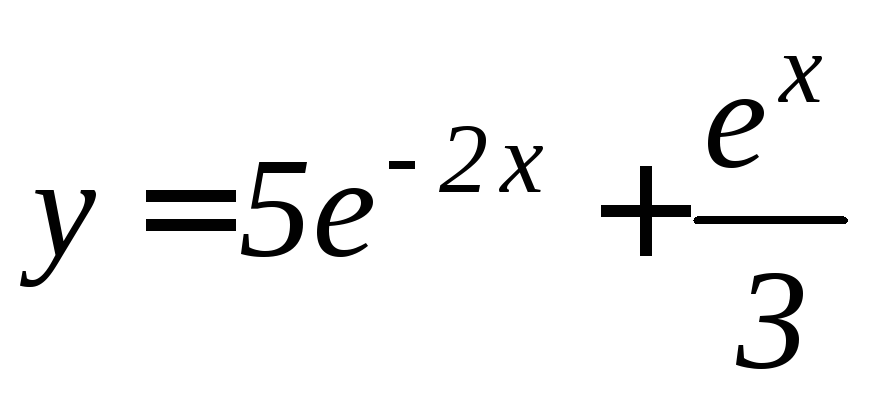
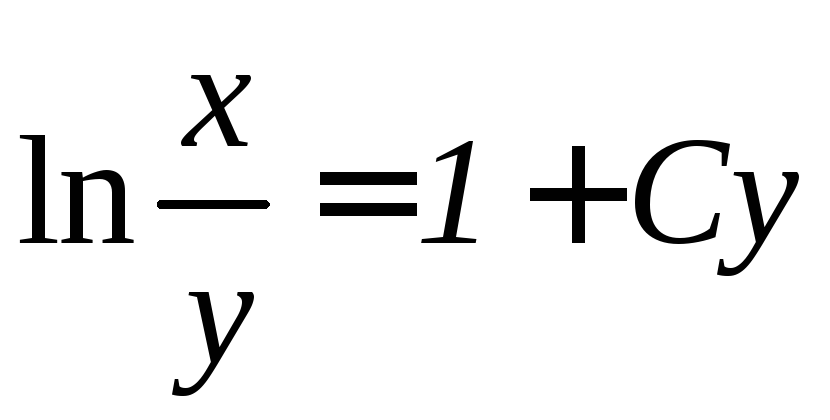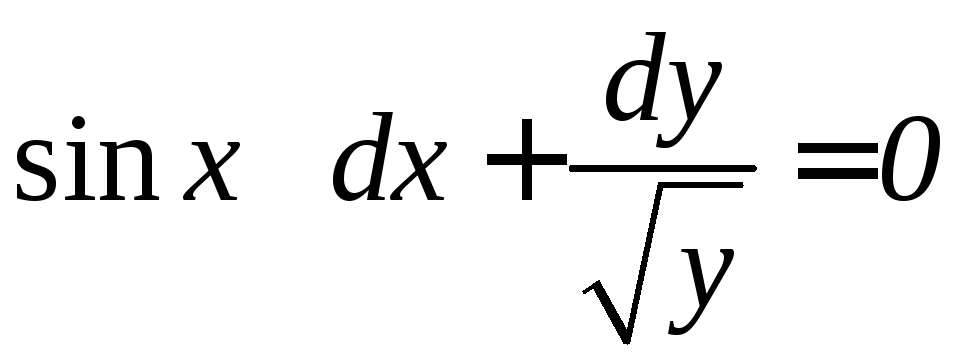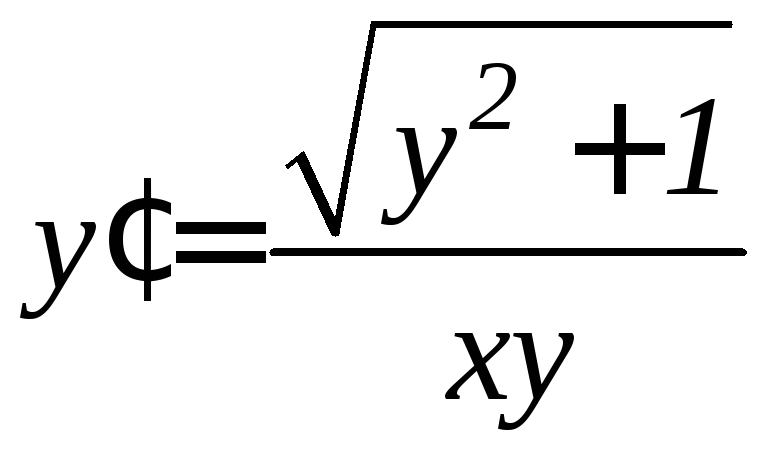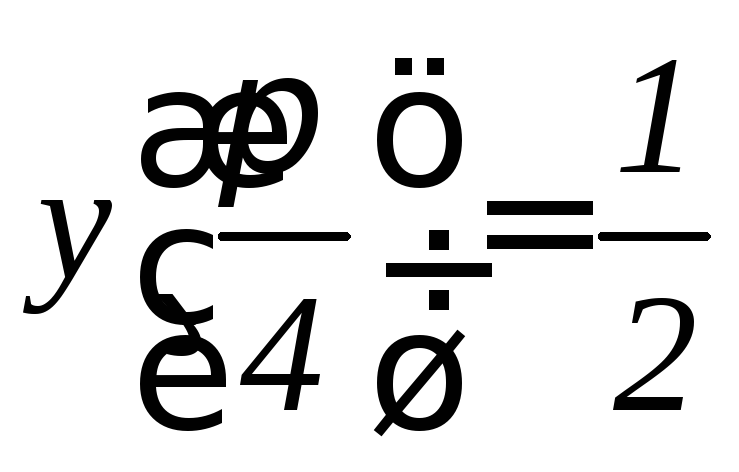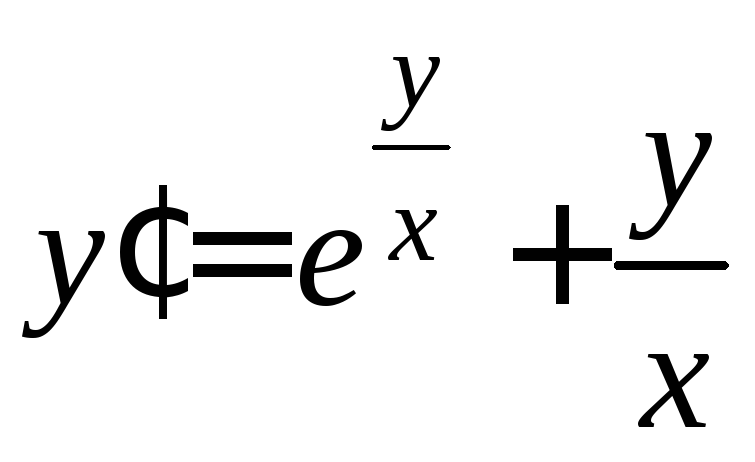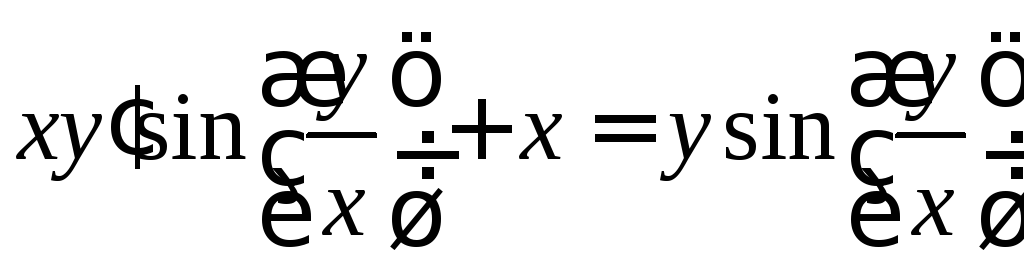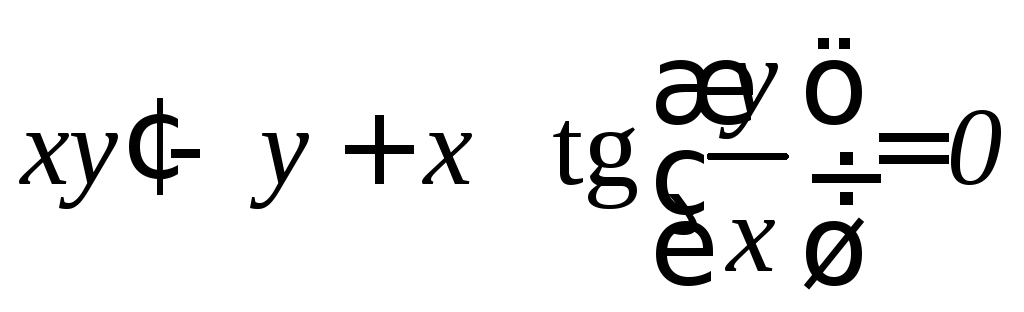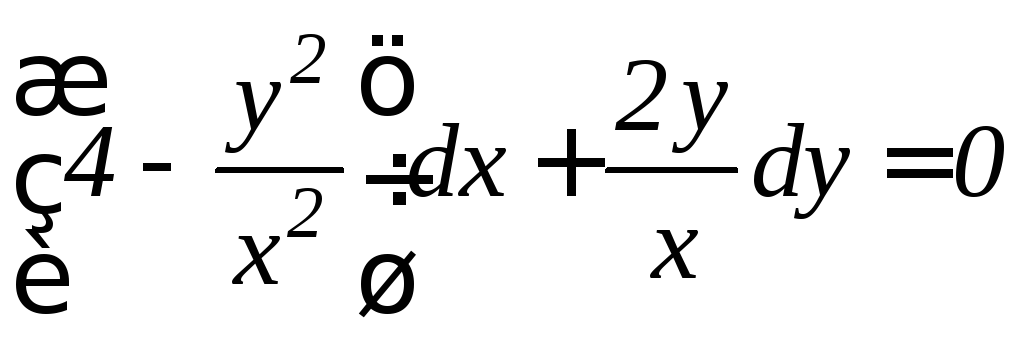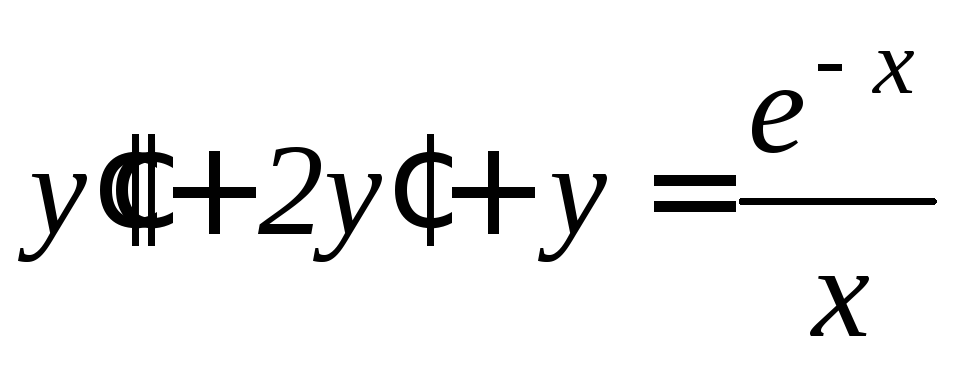
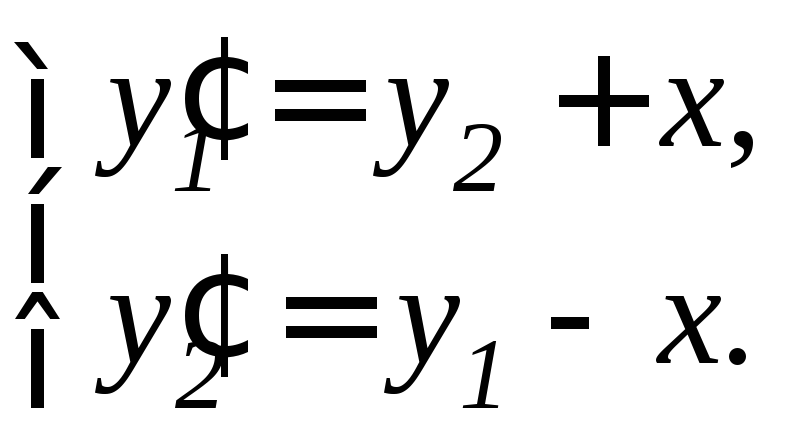
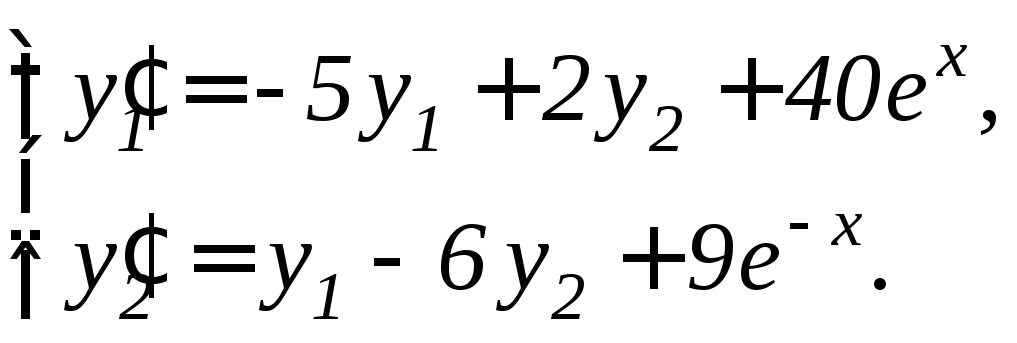
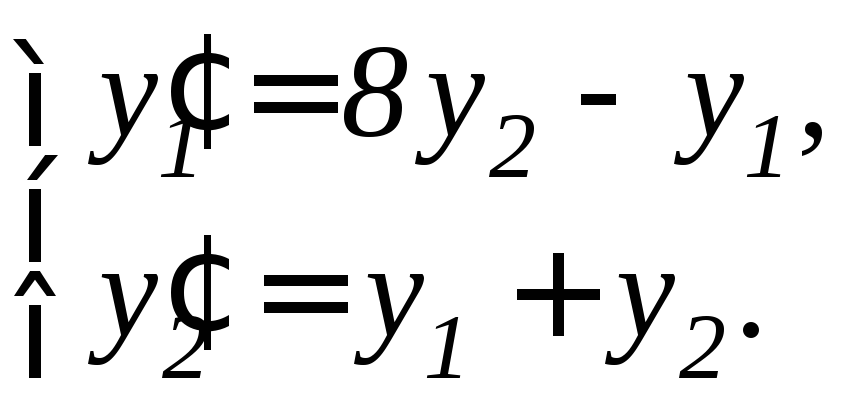
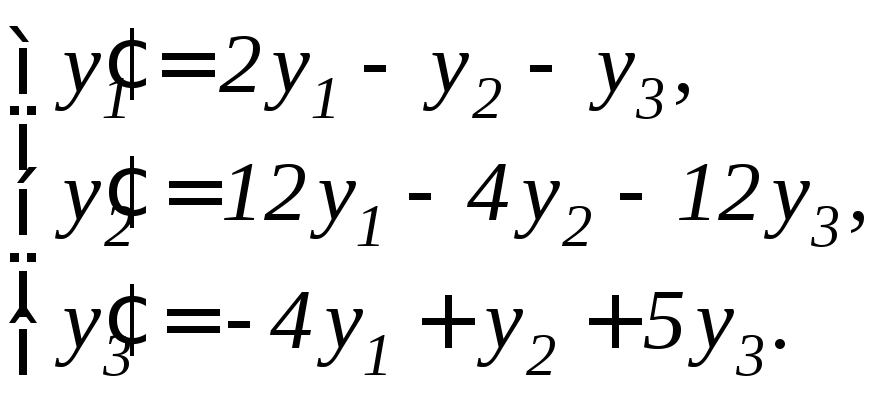
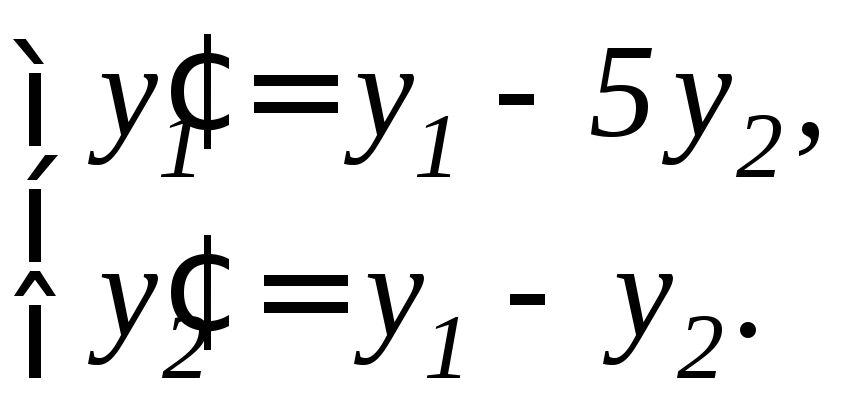
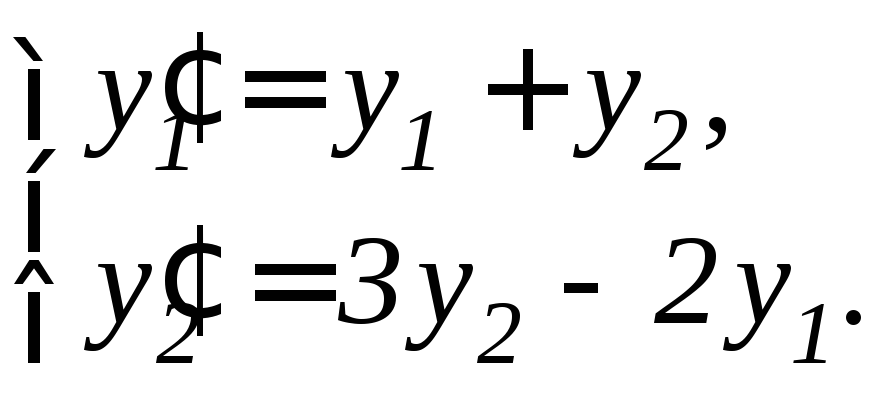
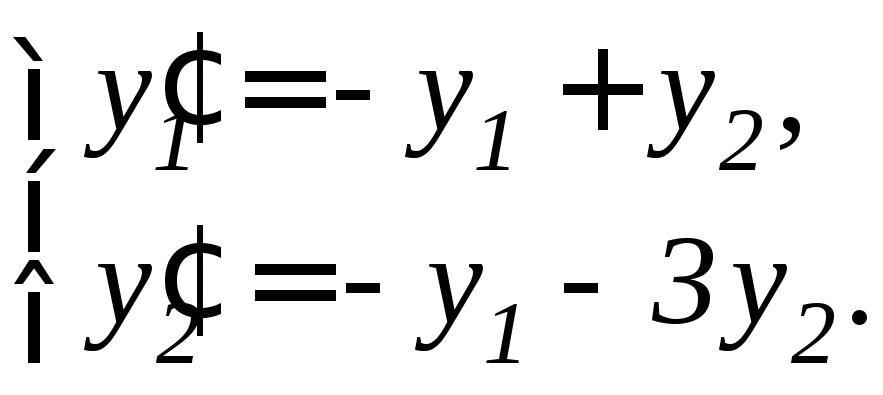
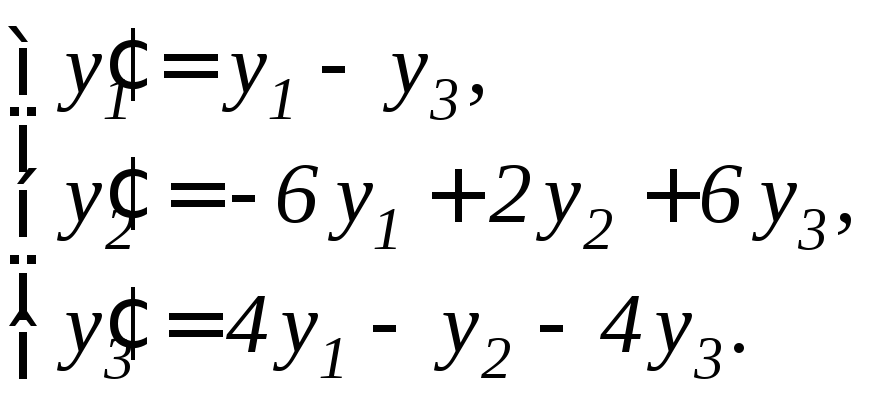
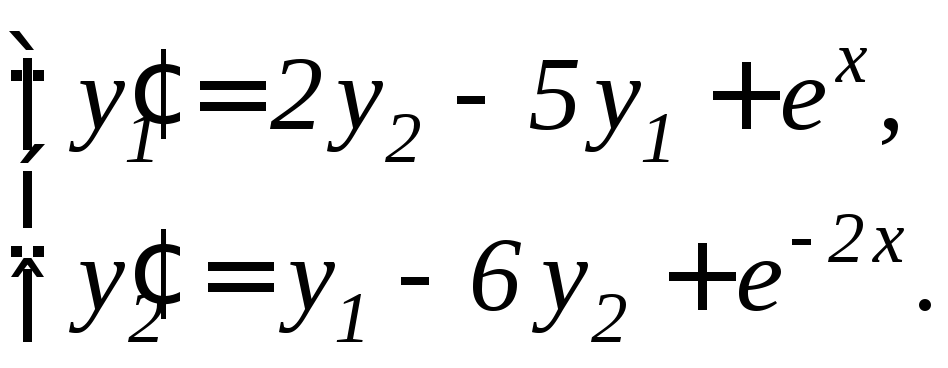
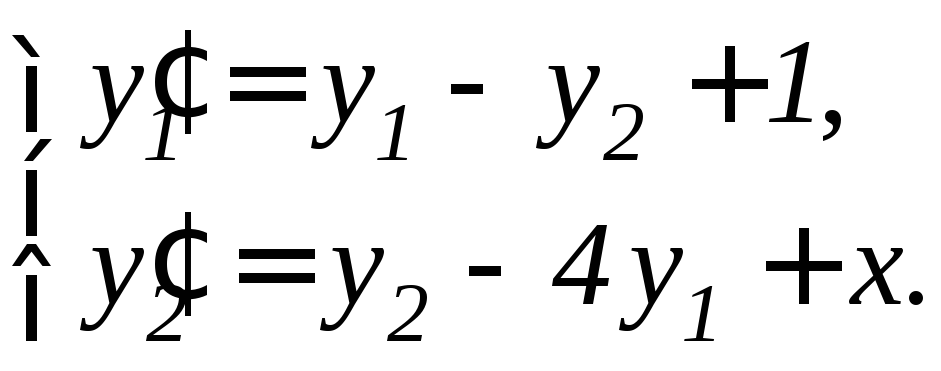
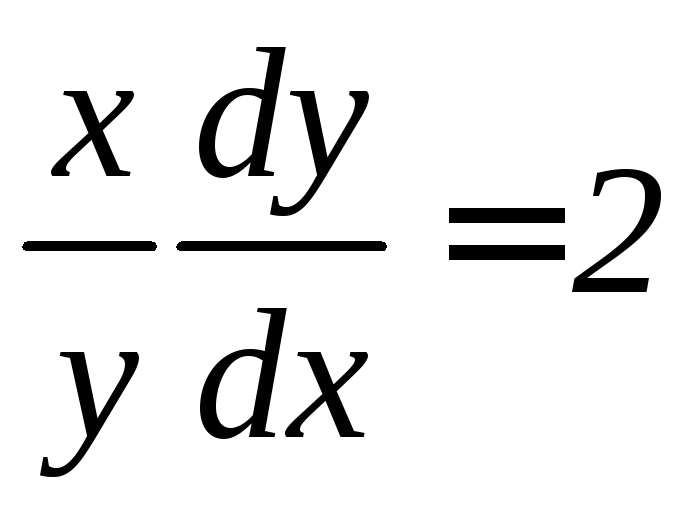
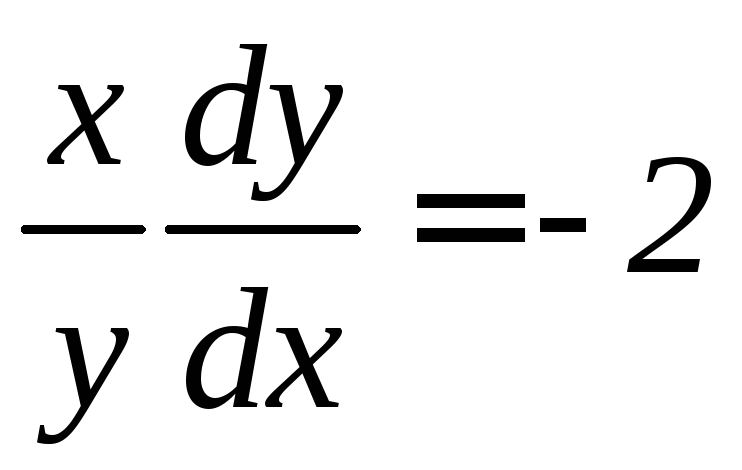
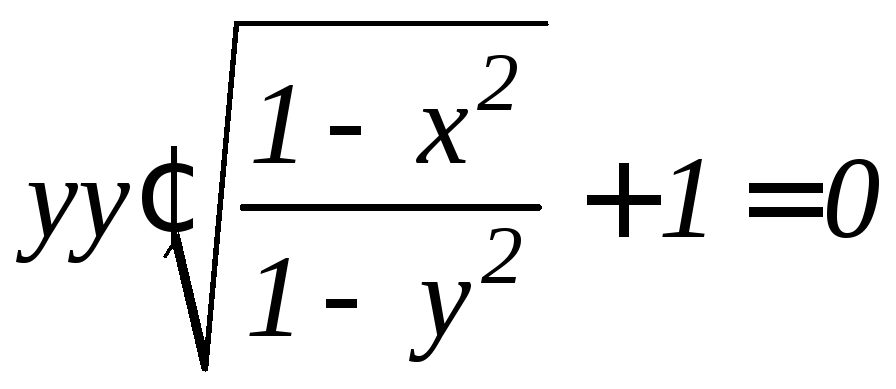
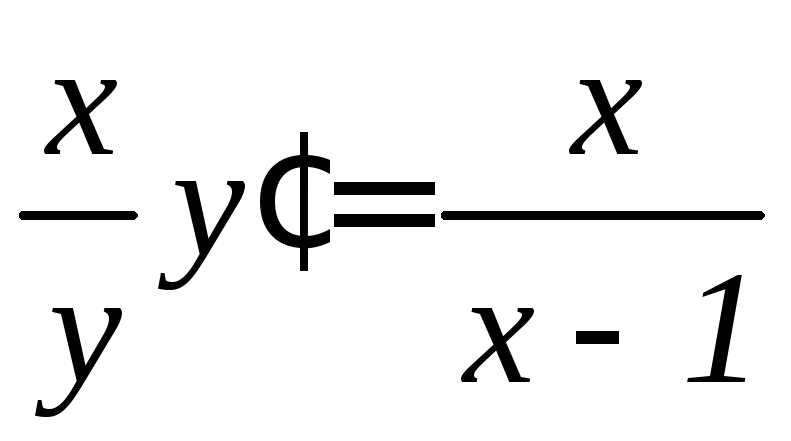
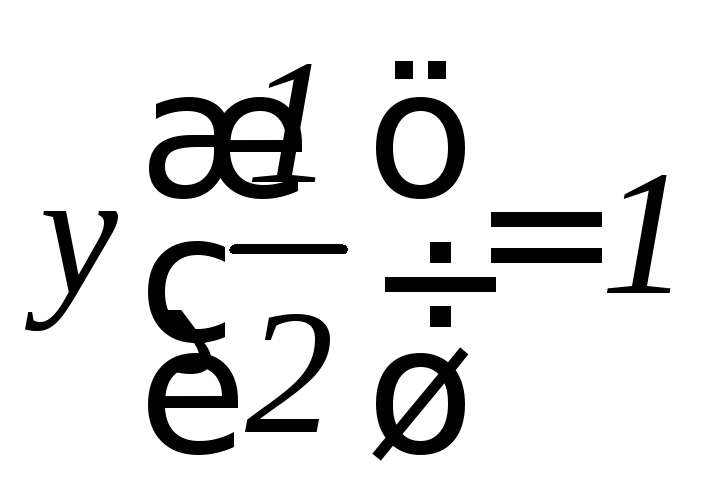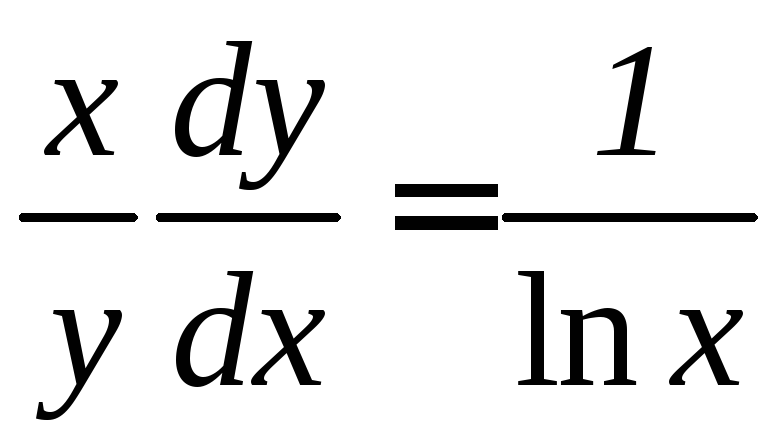
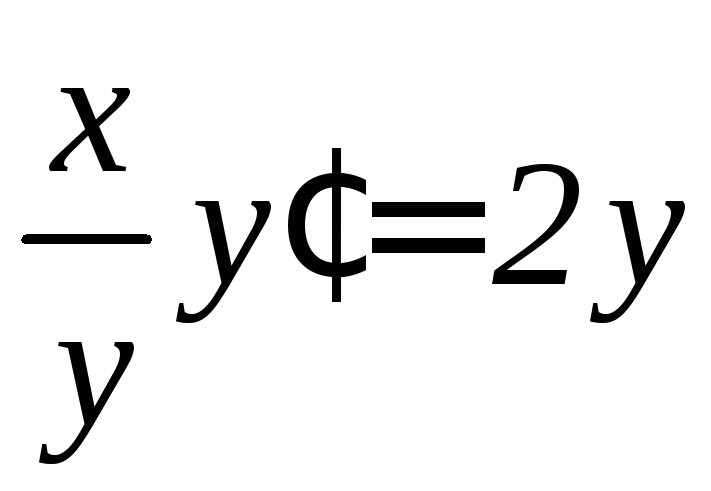
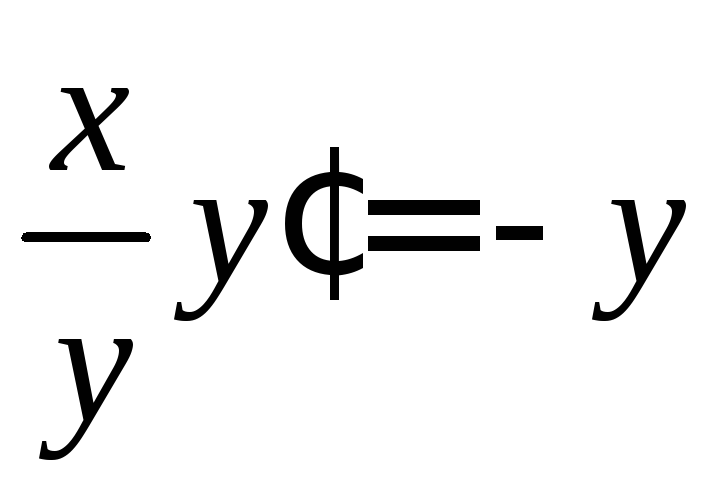
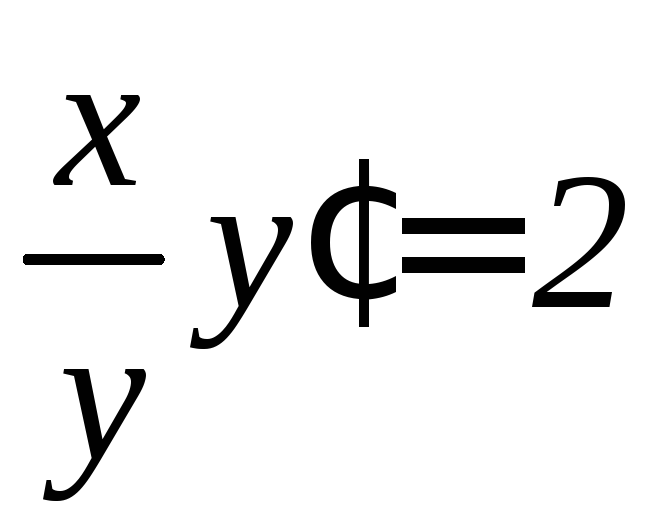
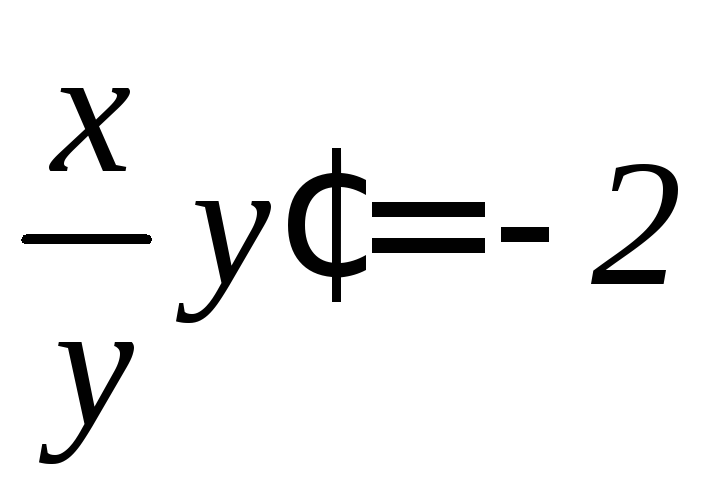
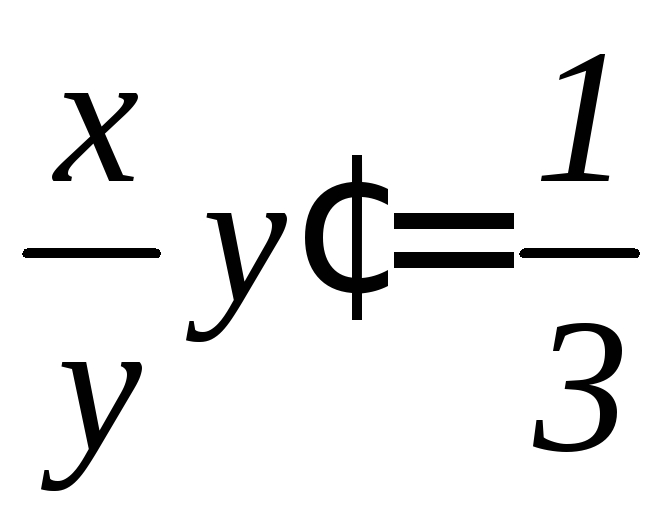
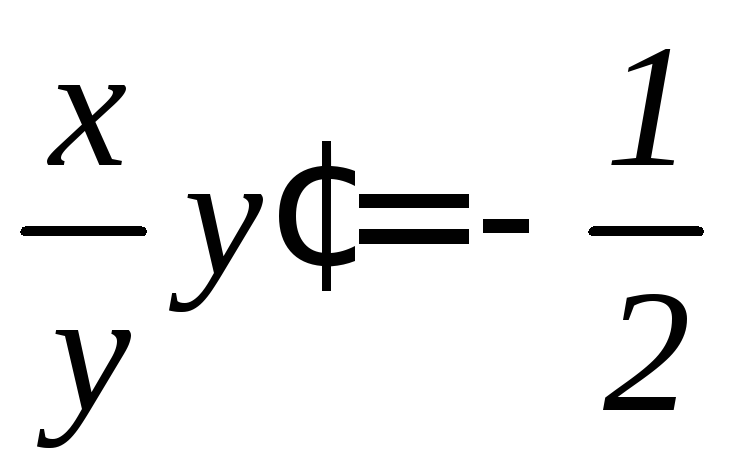
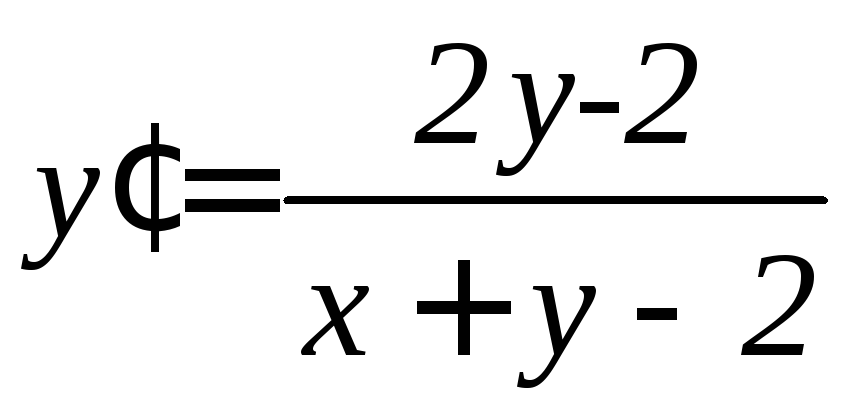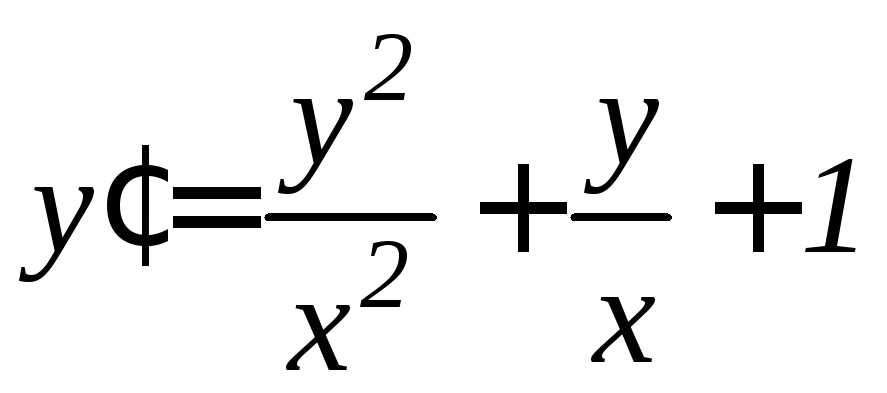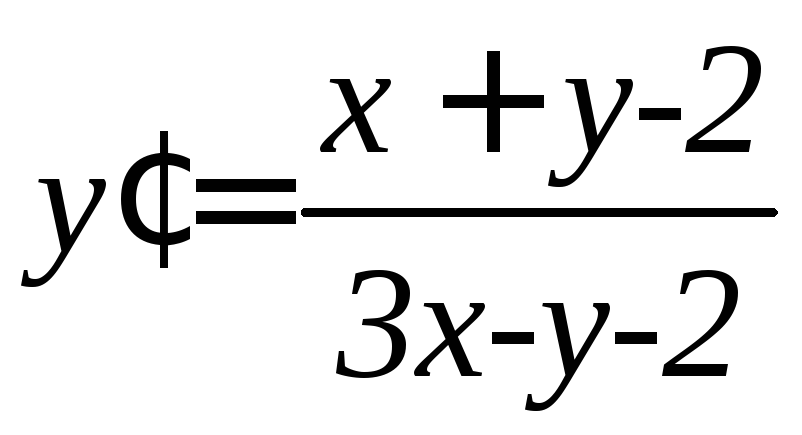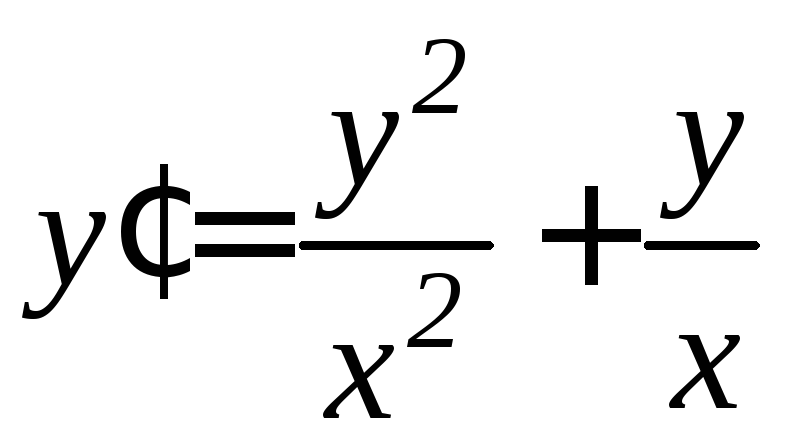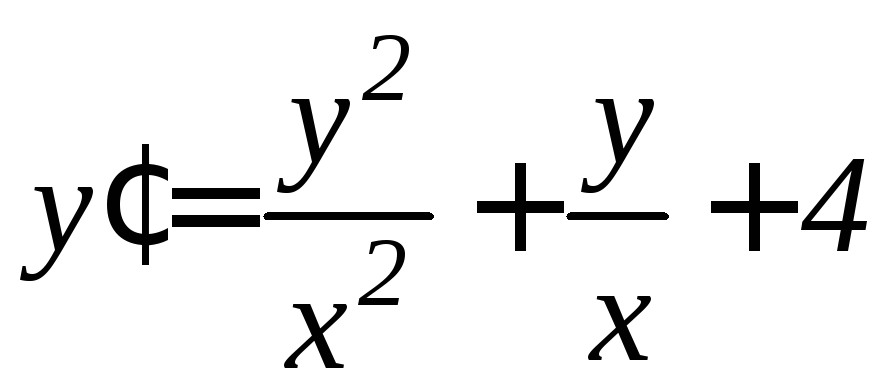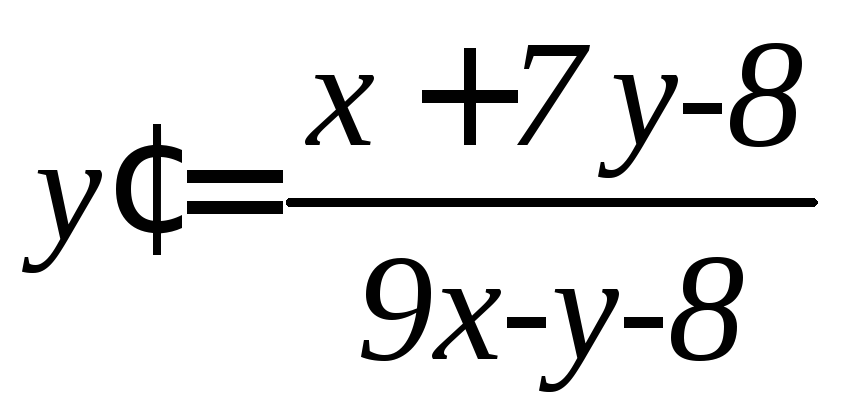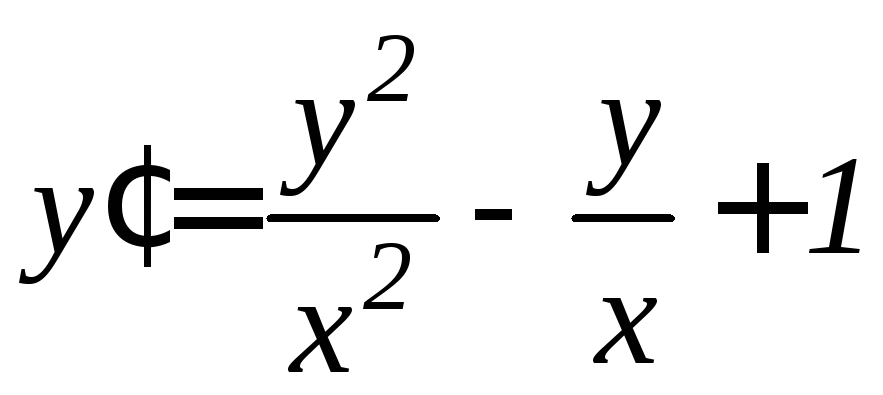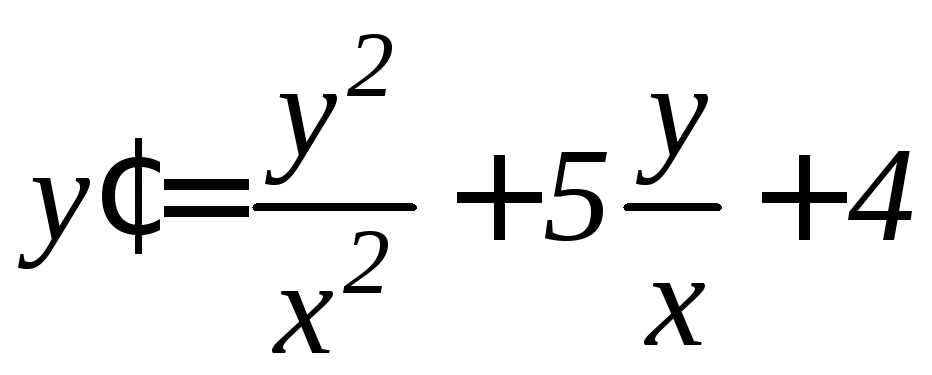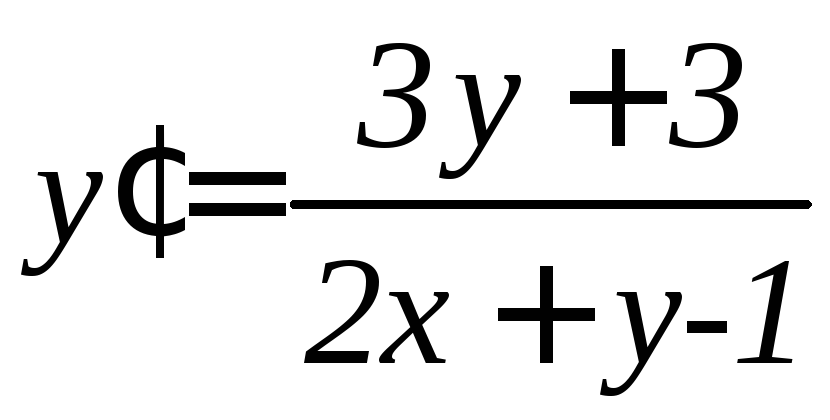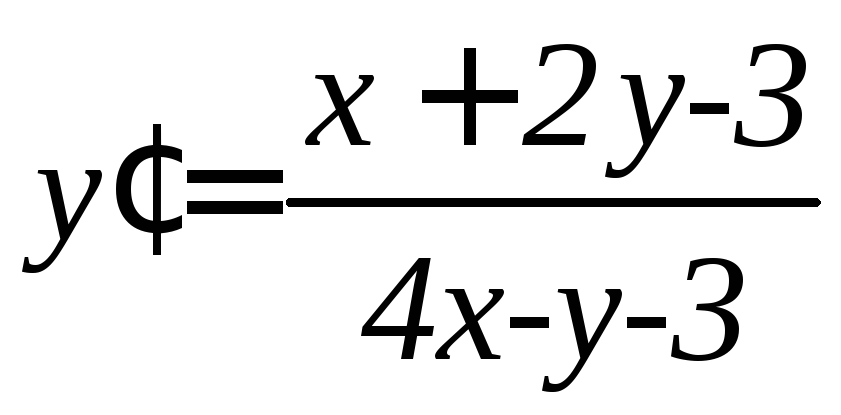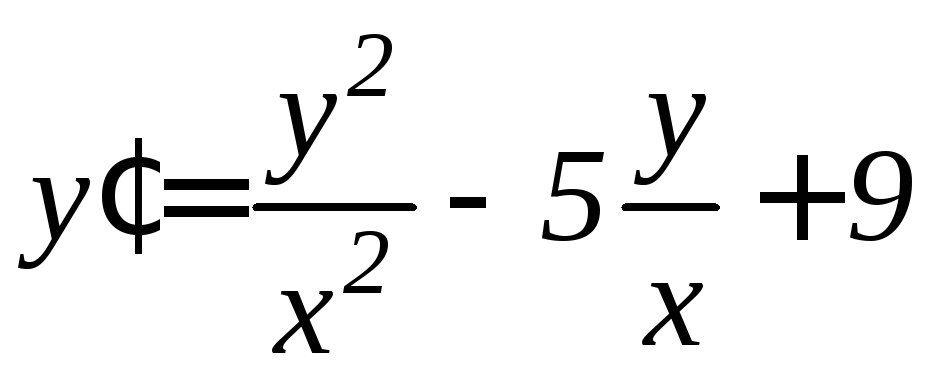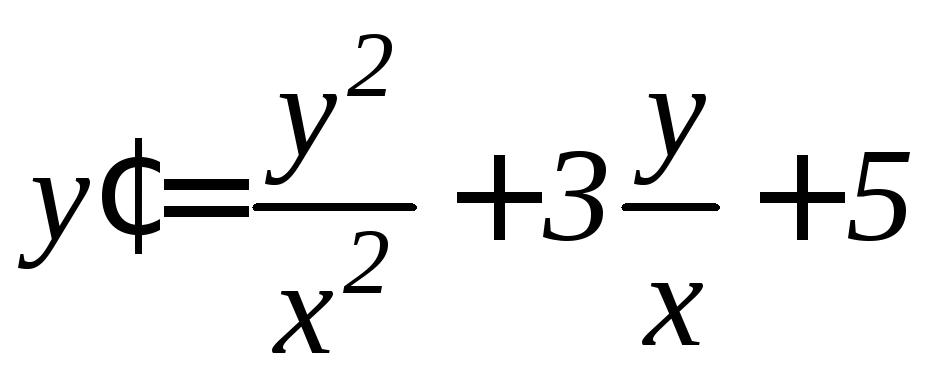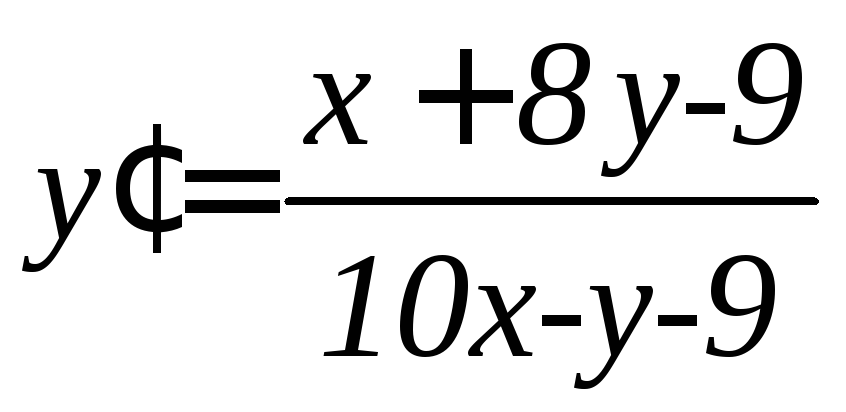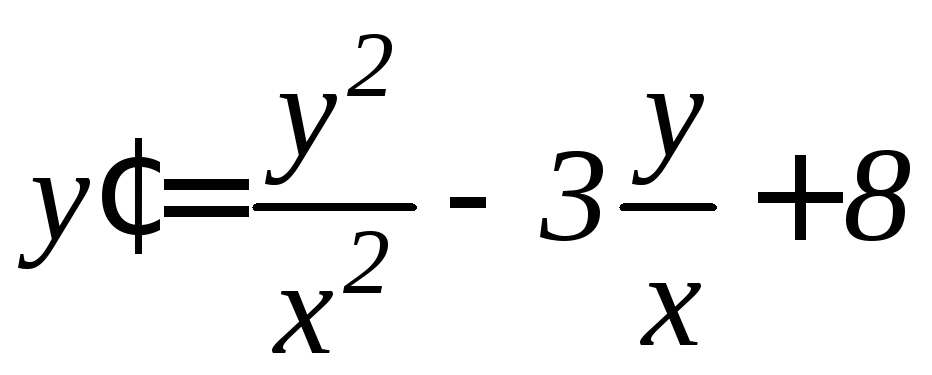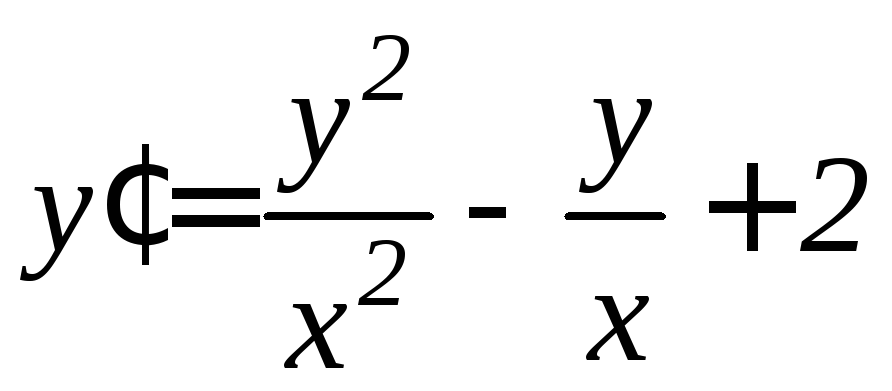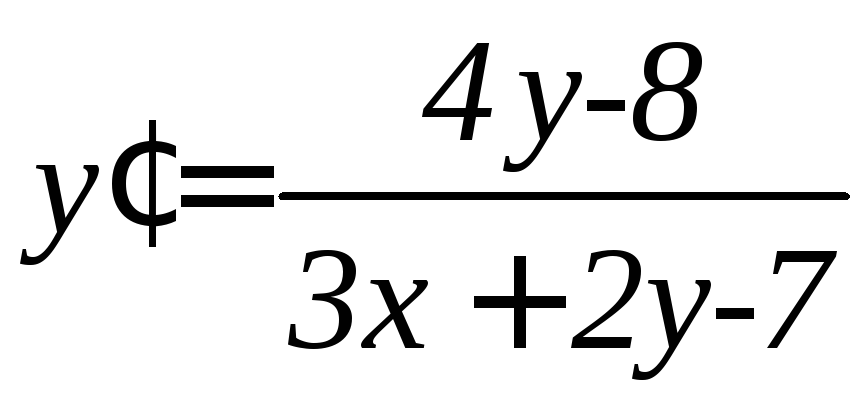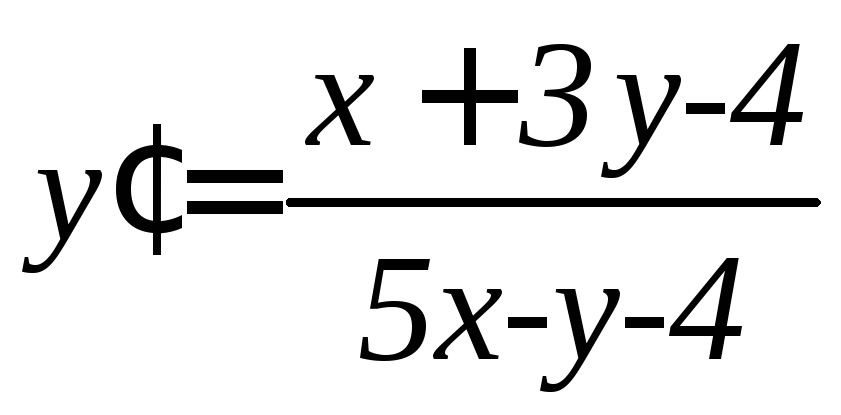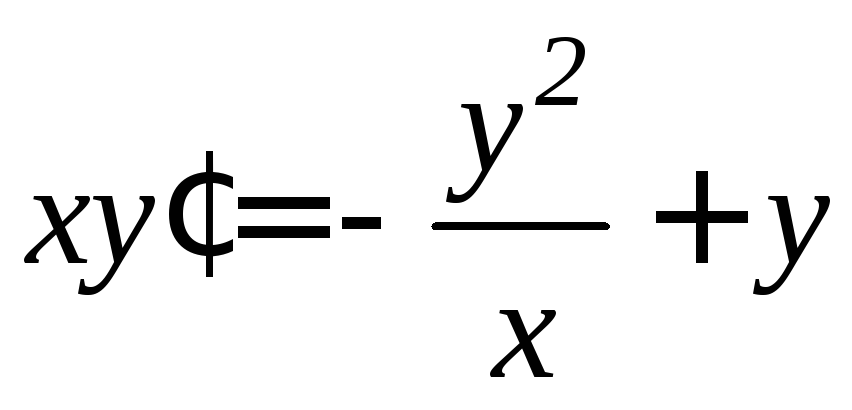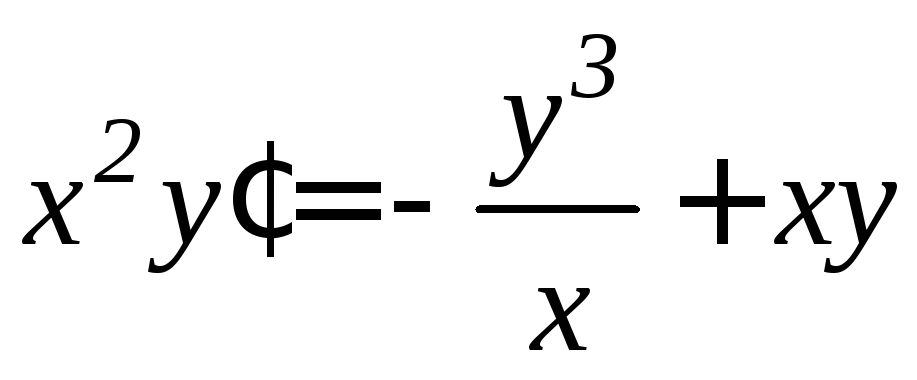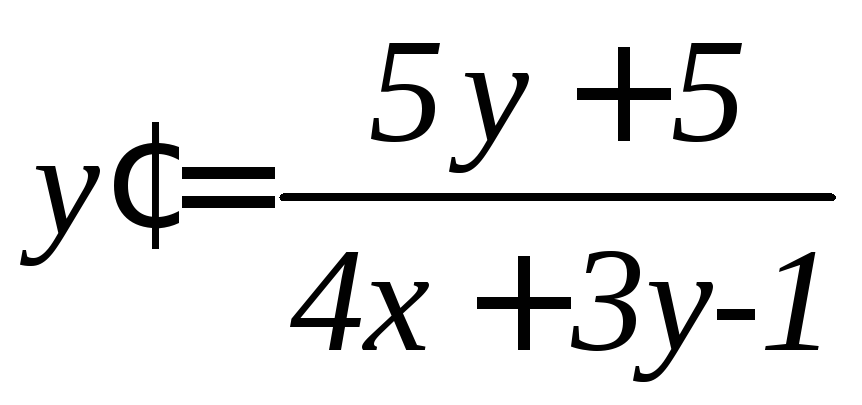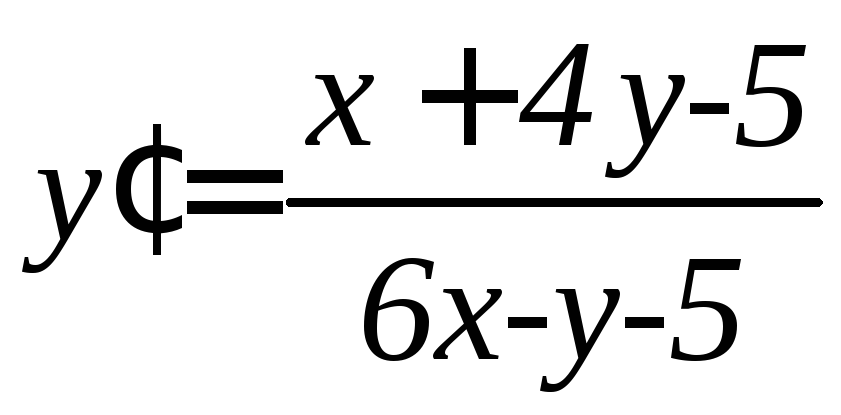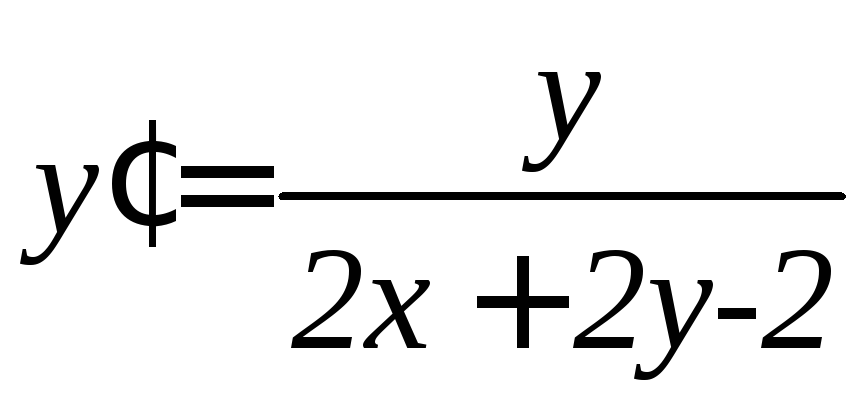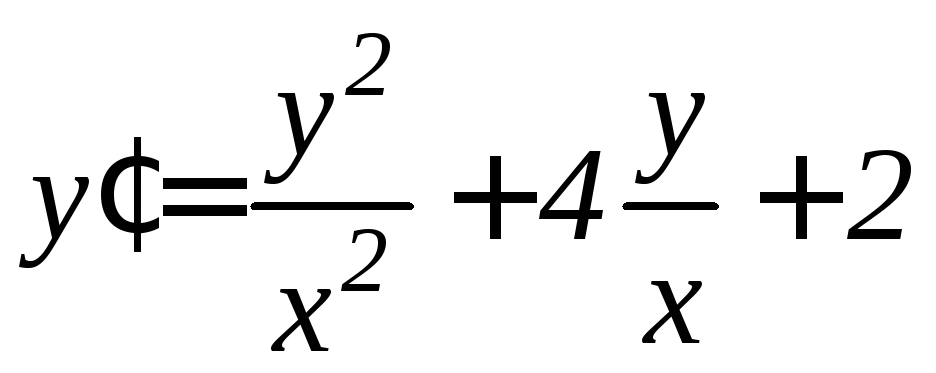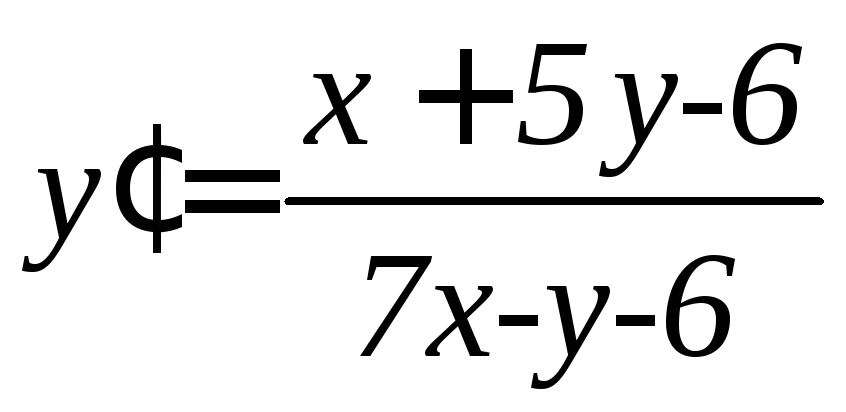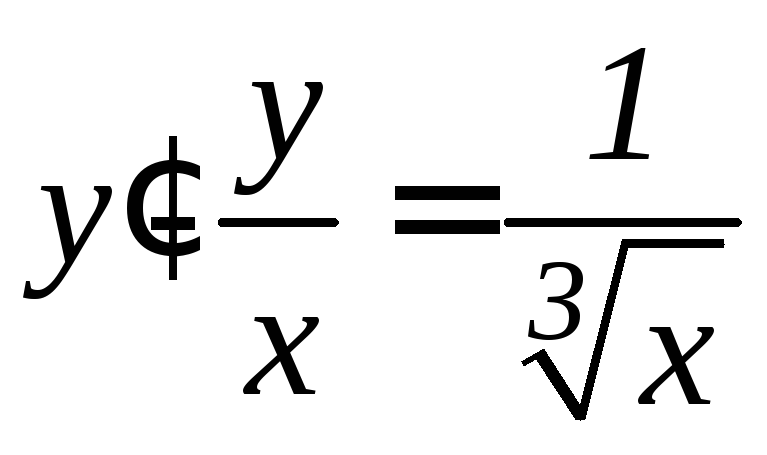
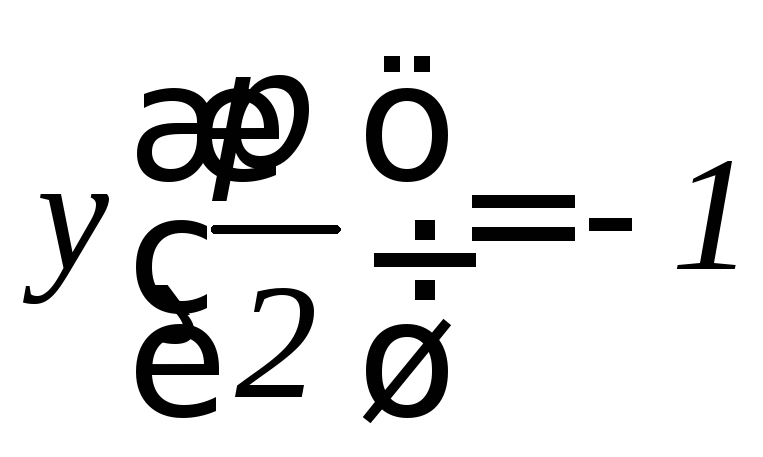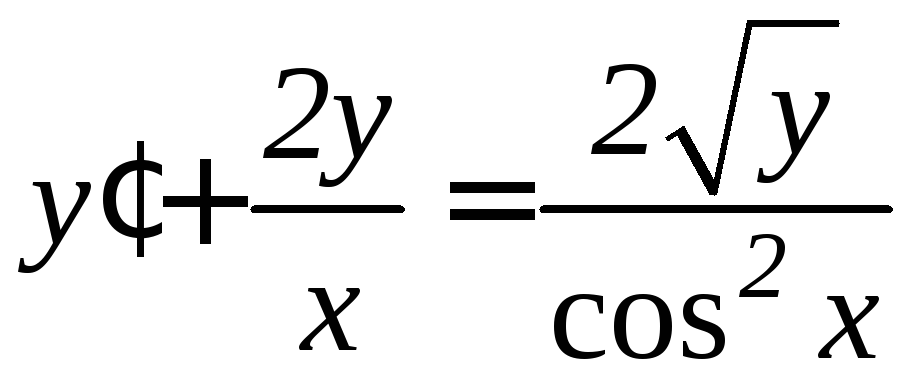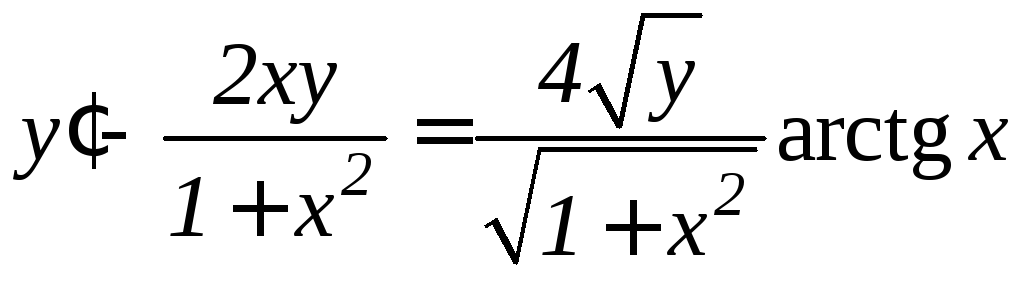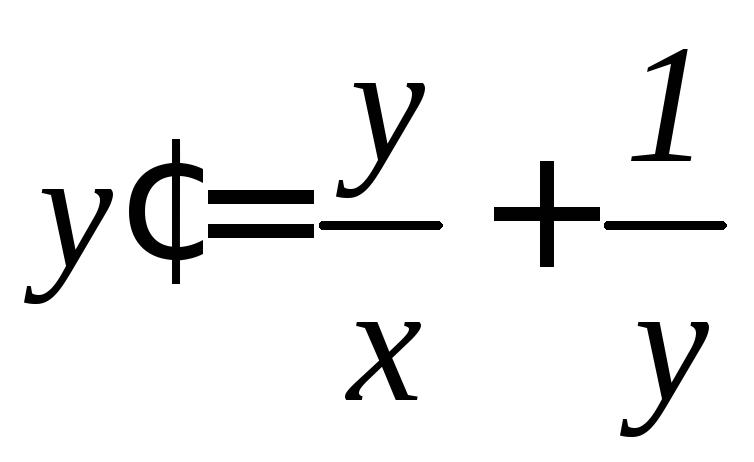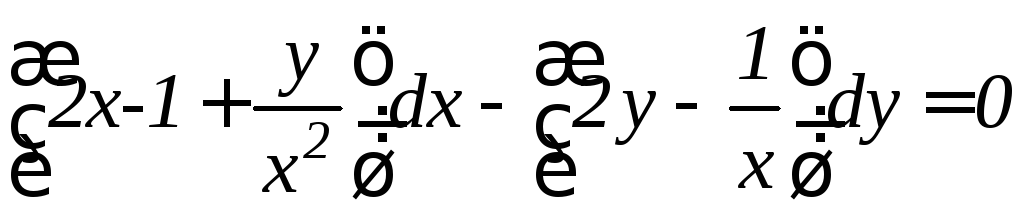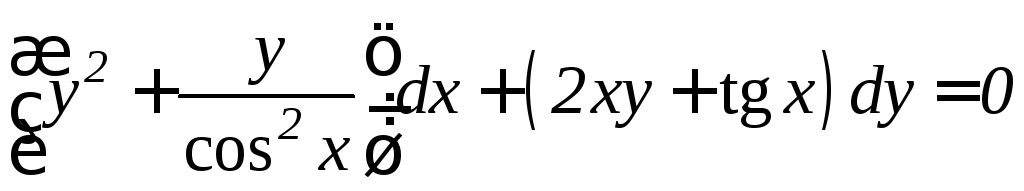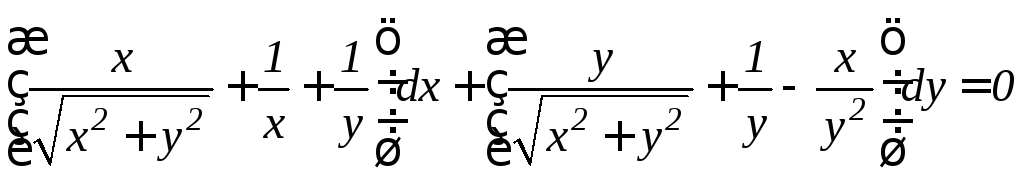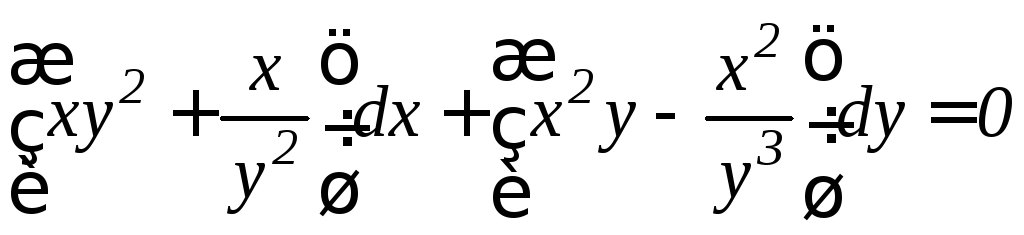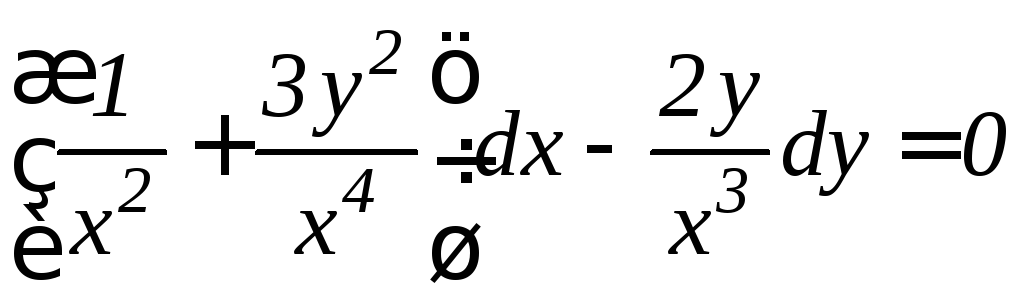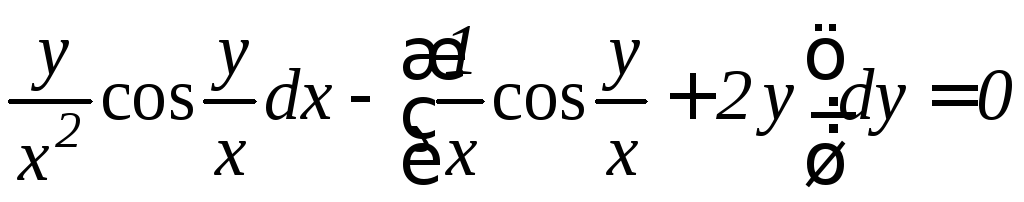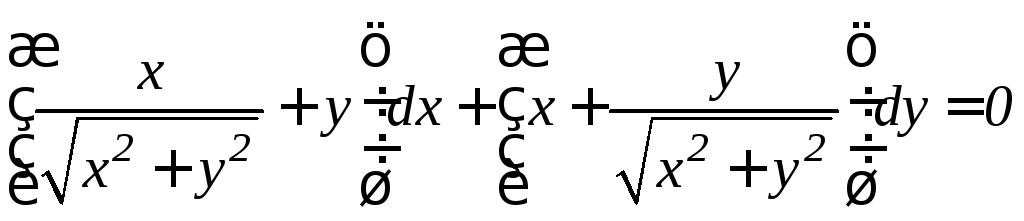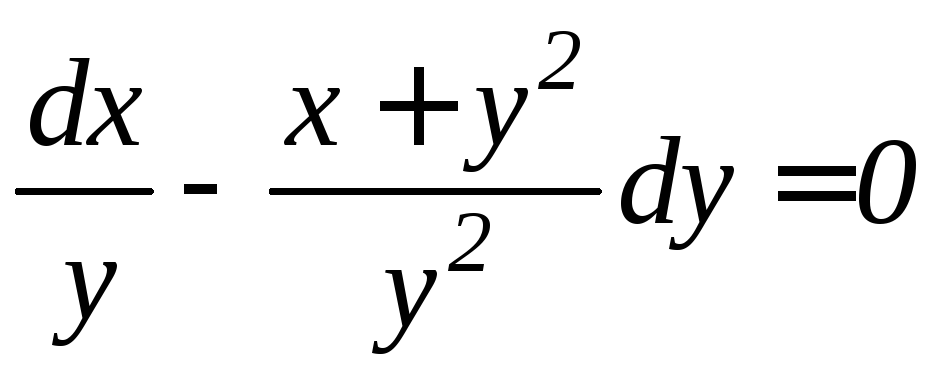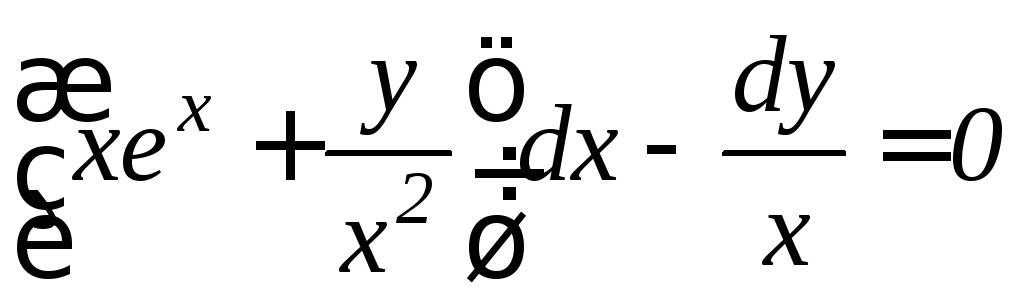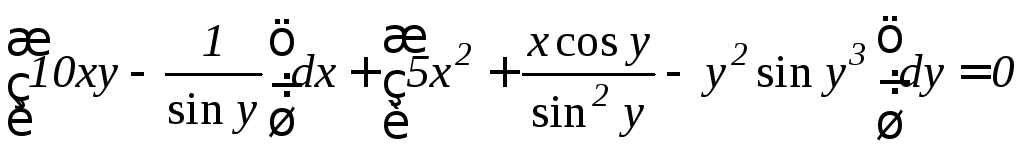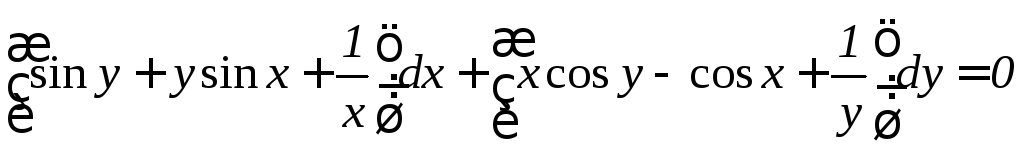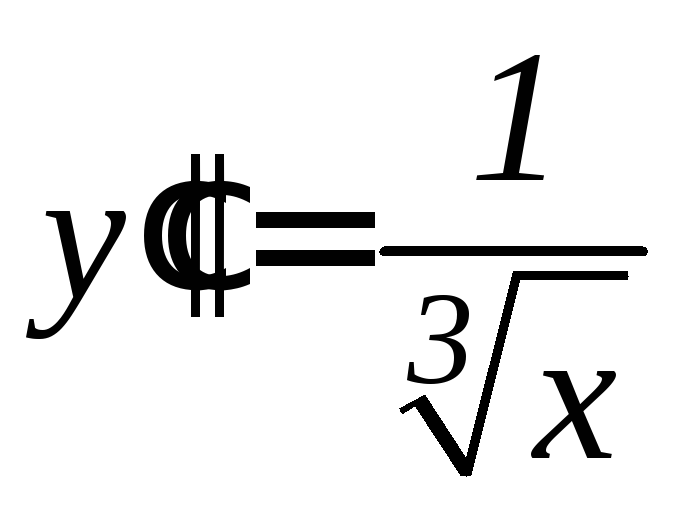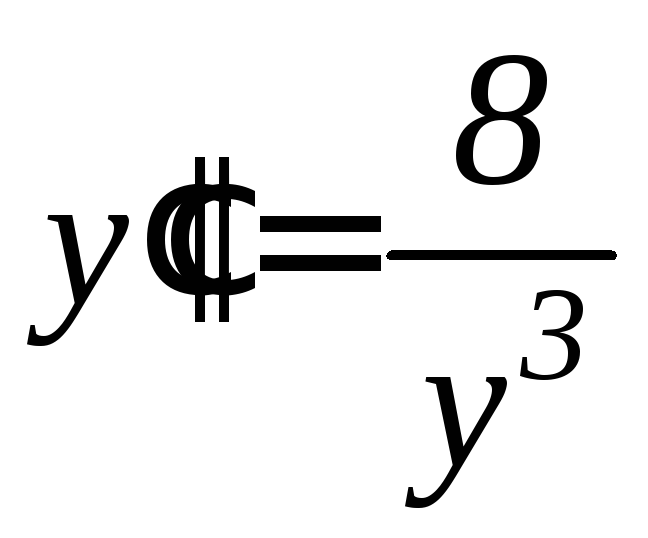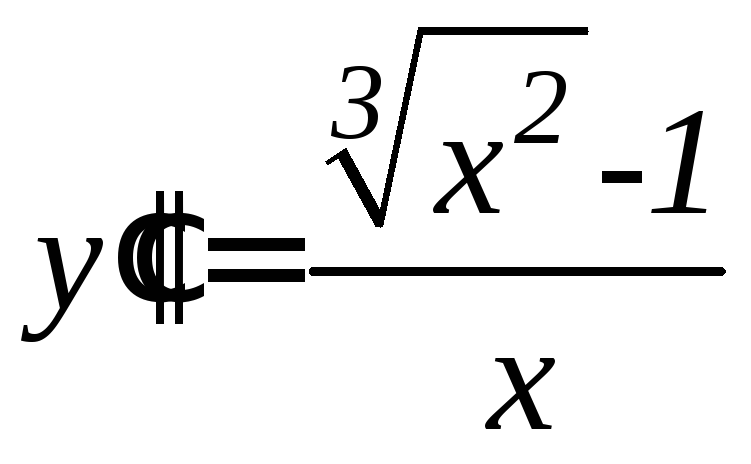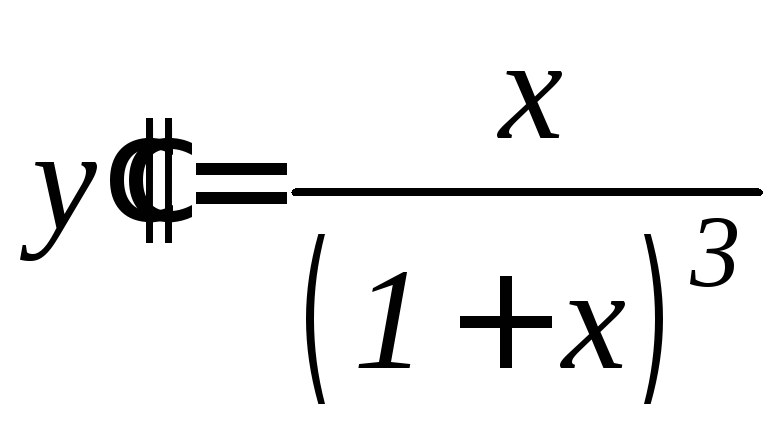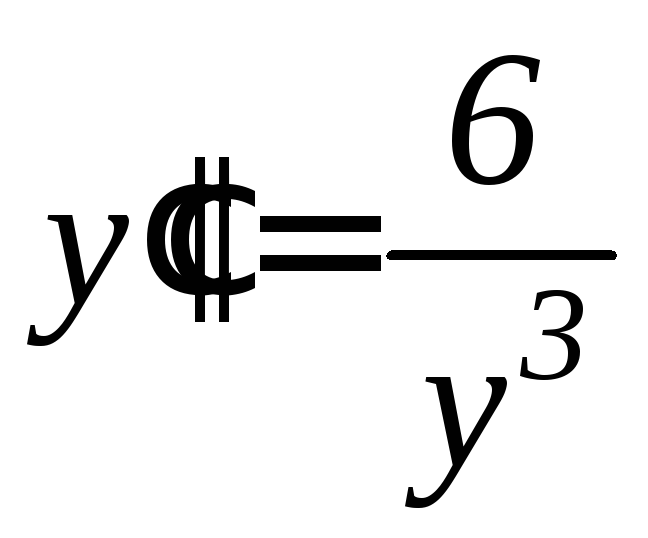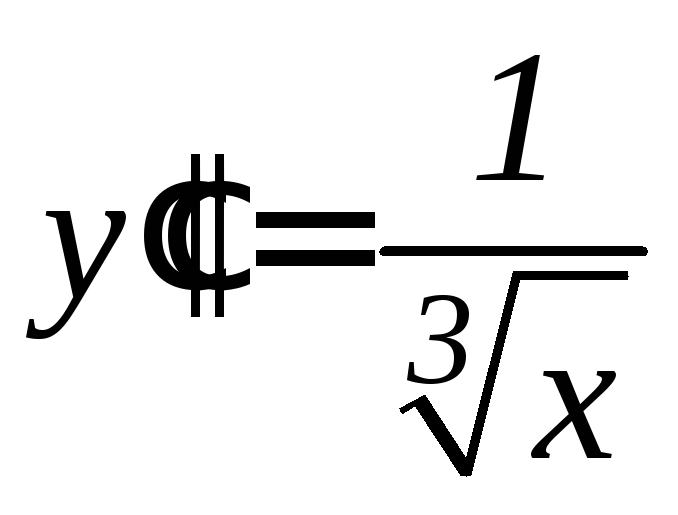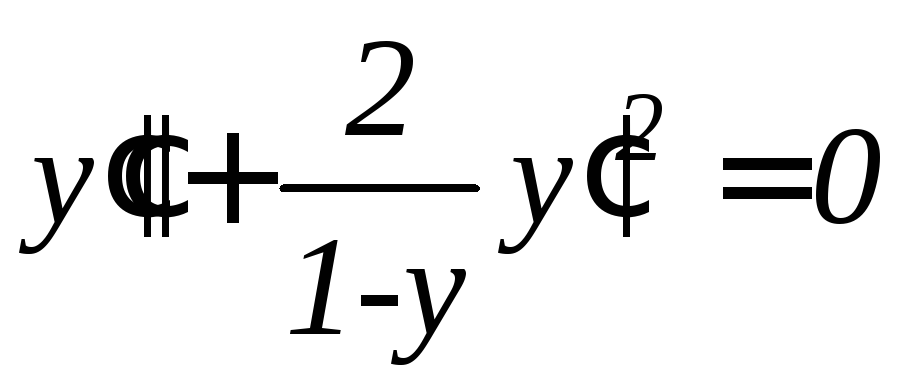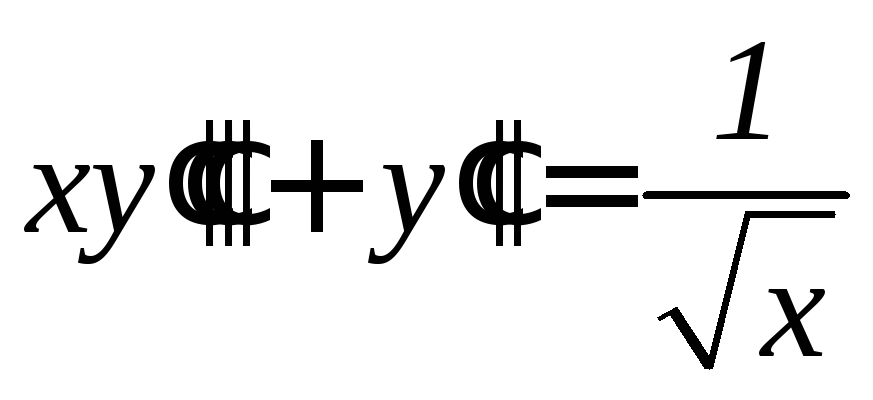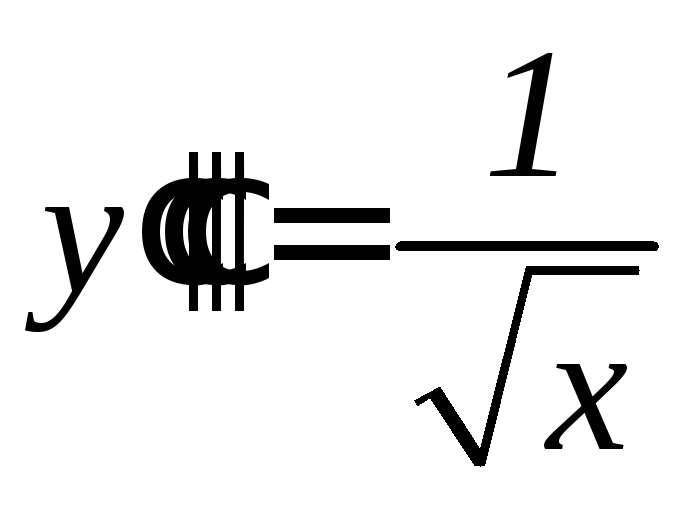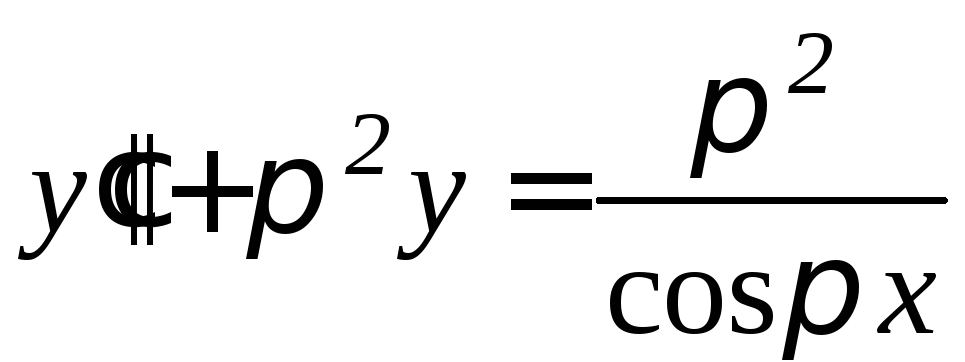
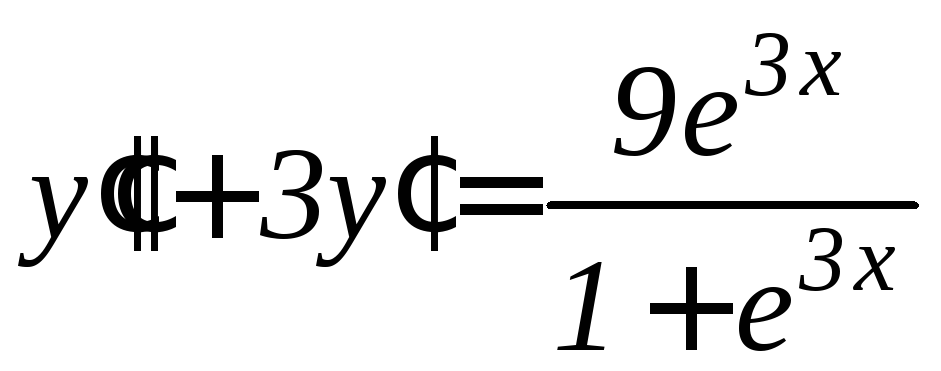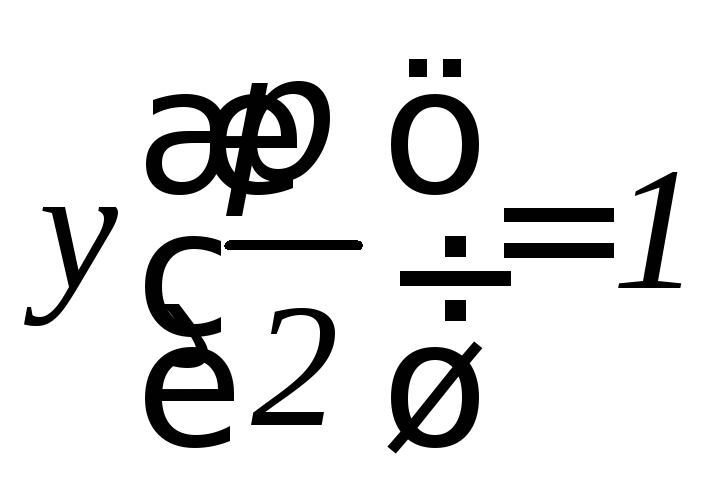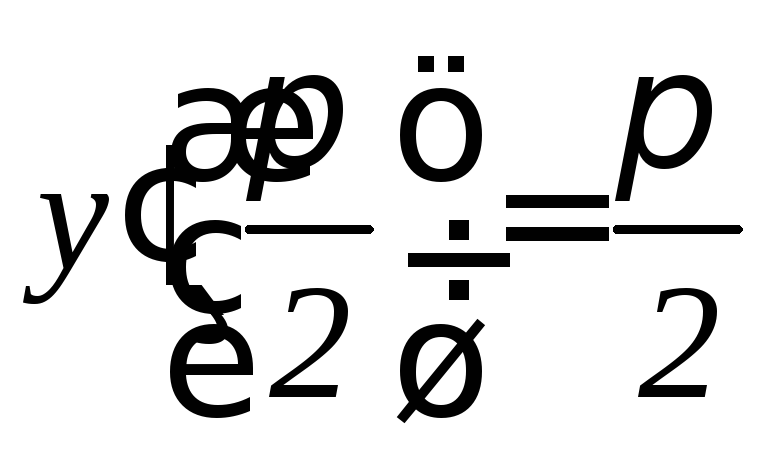
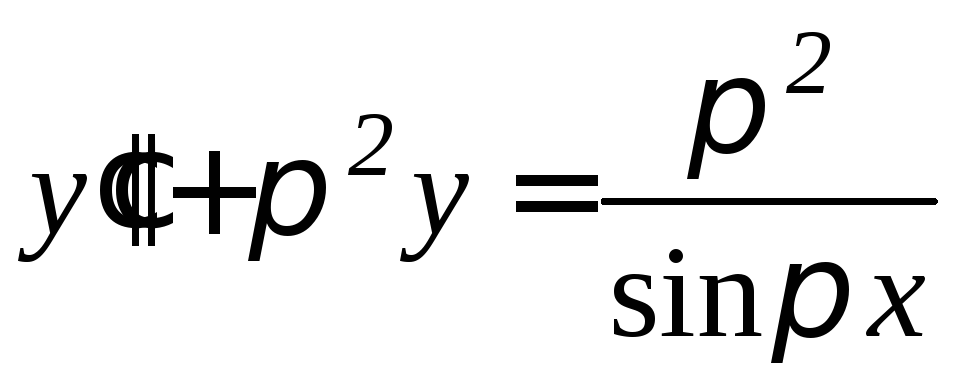
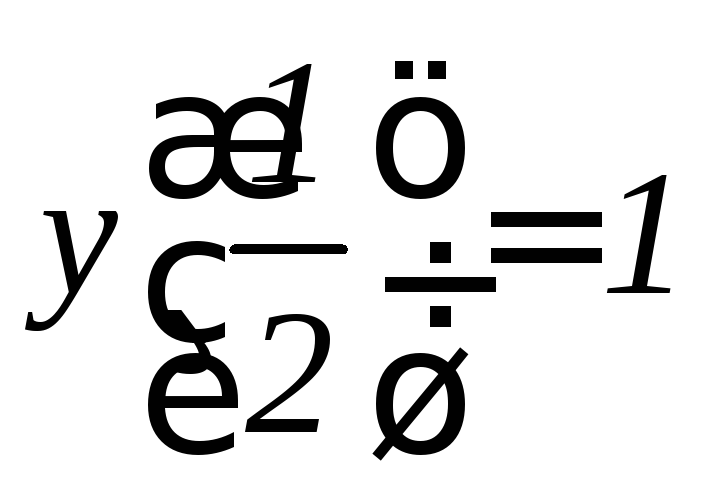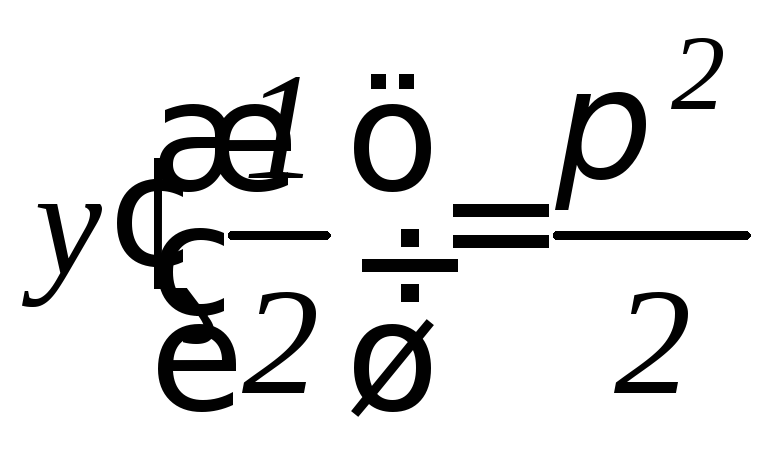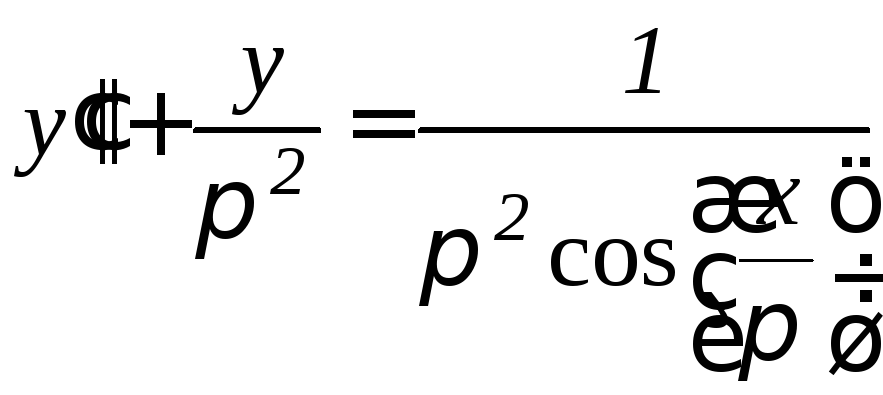
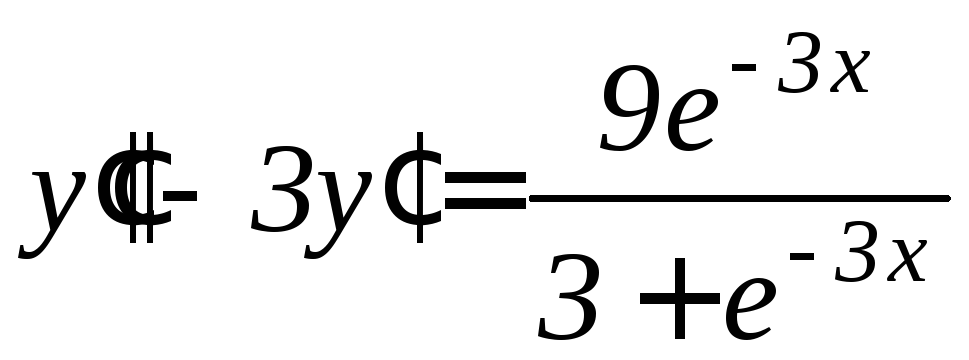
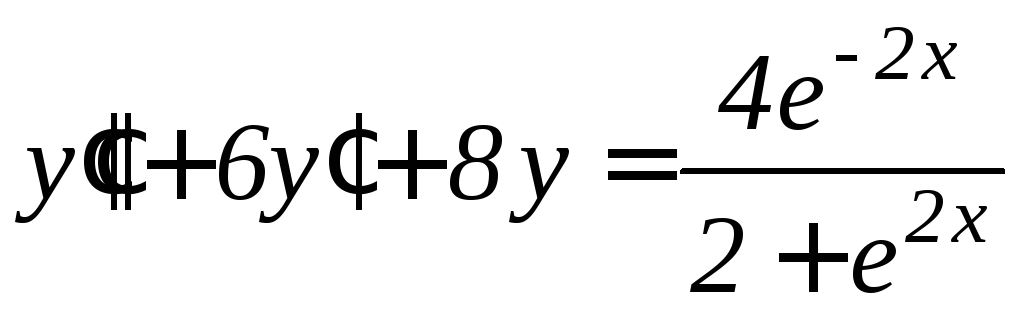
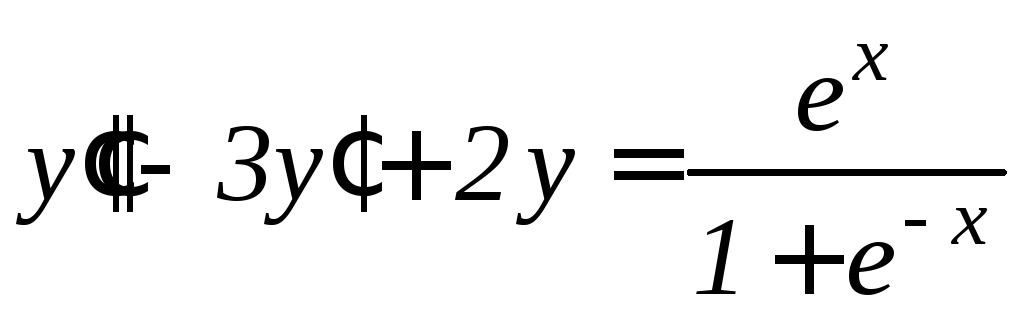
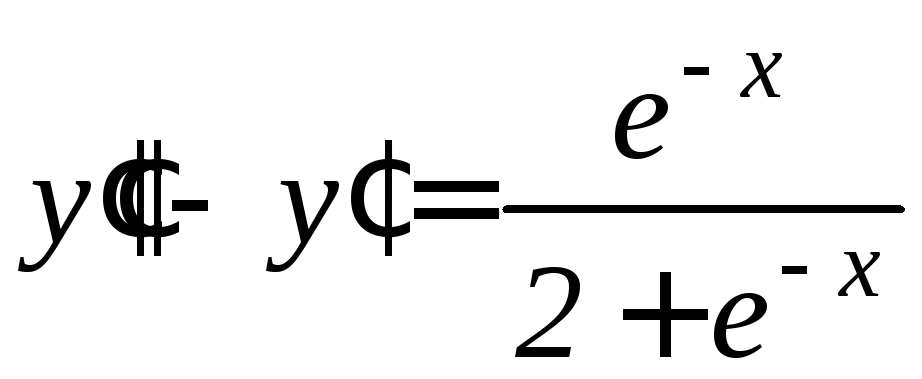
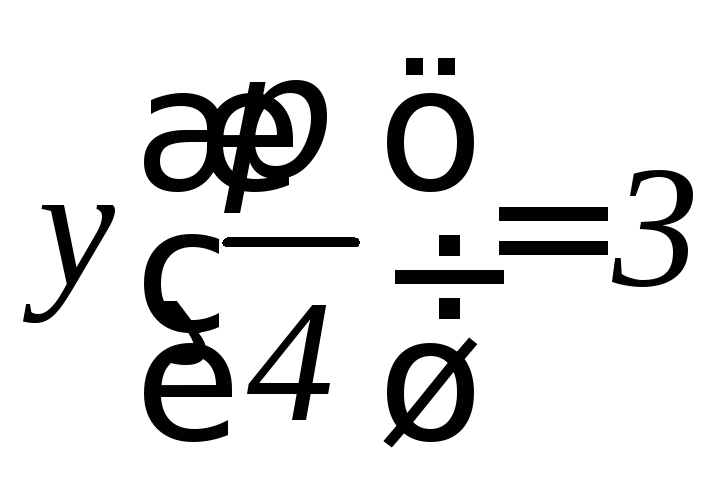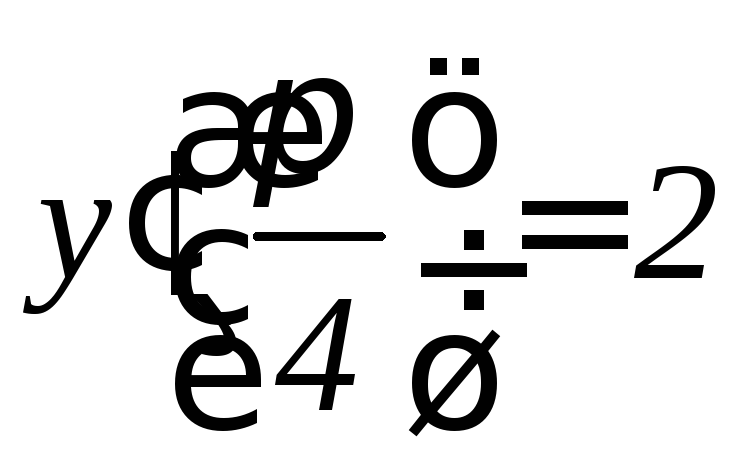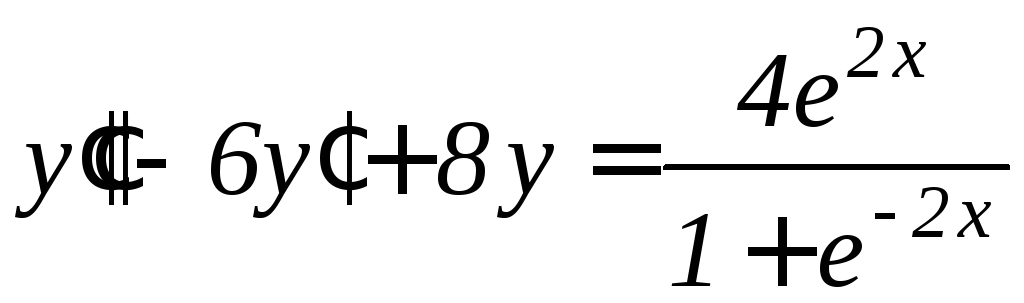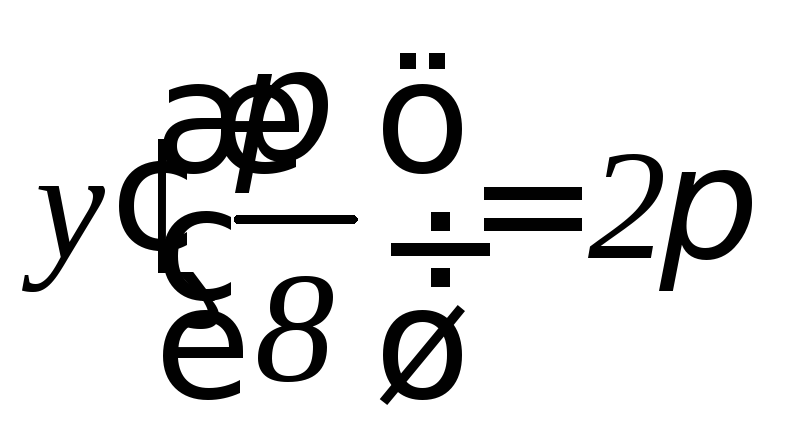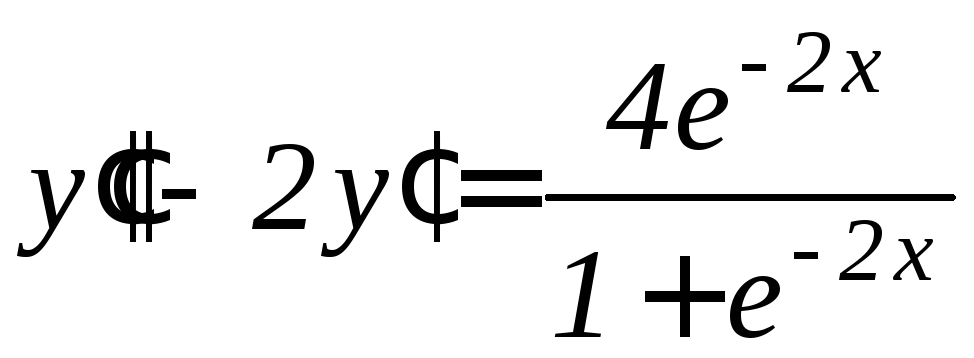
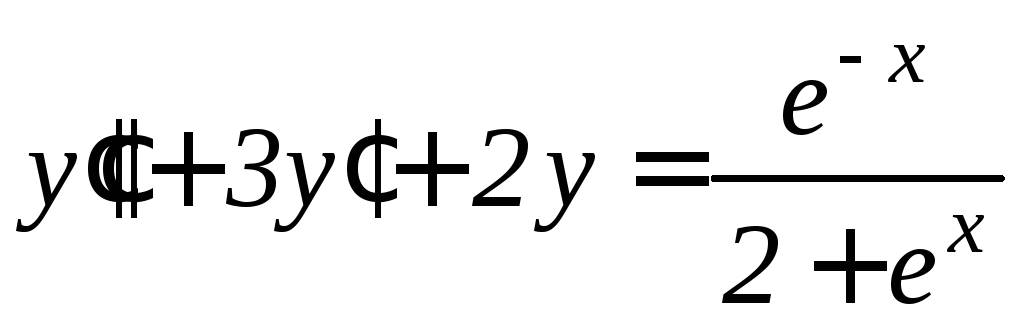
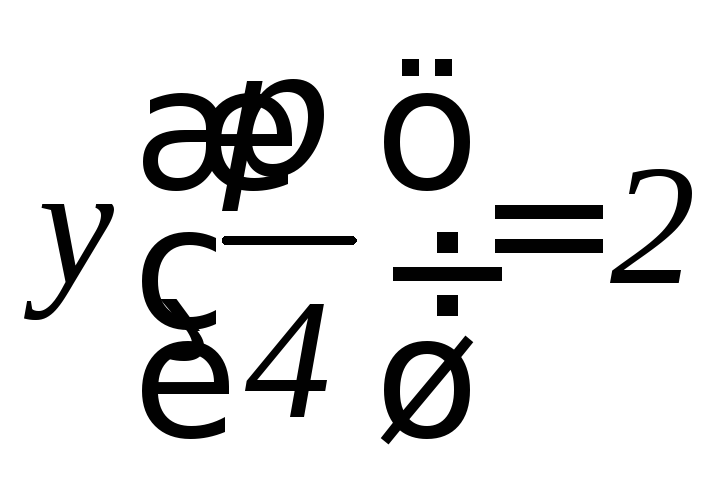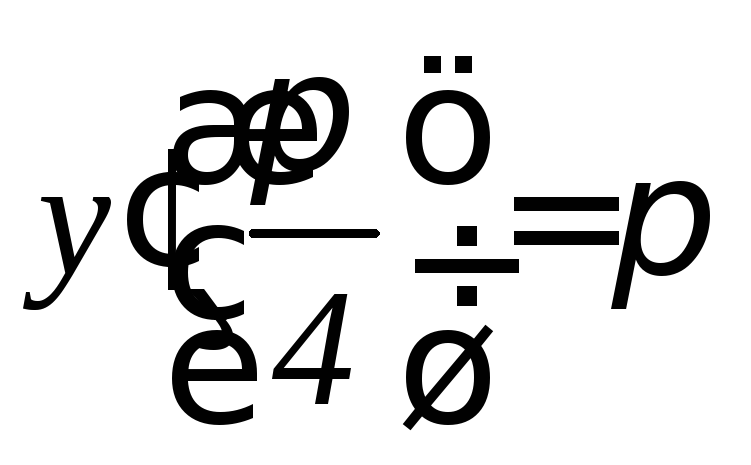