
11. Дифференциальные уравнения
11.1. Дифференциальные уравнения первого порядка
Уравнение вида
![]() ,
,
где
![]() - независимая переменная,
- независимая переменная,![]() - искомая функция,
- искомая функция,![]() - ее производная называется обыкновеннымдифференциальным
уравнением первого порядка.
- ее производная называется обыкновеннымдифференциальным
уравнением первого порядка.
Если это уравнение
можно разрешить относительно
![]() ,
то оно принимает вид
,
то оно принимает вид
![]() (11.1)
(11.1)
и называется уравнением первого порядка, разрешенным относительно производной.
Решением
дифференциального уравнения
называется дифференцируемая функция
![]() ,
,![]() ,
которая при подстановке в уравнение
вместо неизвестной функции обращает
его в тождество.
,
которая при подстановке в уравнение
вместо неизвестной функции обращает
его в тождество.
График решения дифференциального уравнения называется интегральной кривой.
Условия
![]() при
при
![]() ,
(11.2)
,
(11.2)
при которых функция
![]() принимает заданное значение
принимает заданное значение![]() в заданной точке
в заданной точке![]() ,
называютначальным
условием.
,
называютначальным
условием.
Общим решением
уравнения(11.1) в некоторой области![]() плоскости
плоскости![]() называется функция
называется функция![]() ,
зависящая от
,
зависящая от![]() и произвольной постоянной
и произвольной постоянной![]() и обладающая следующими свойствами:
и обладающая следующими свойствами:
она является решением уравнения (11.1) при любом значении постоянной
 ;
;при любых начальных условиях (11.2) таких, что
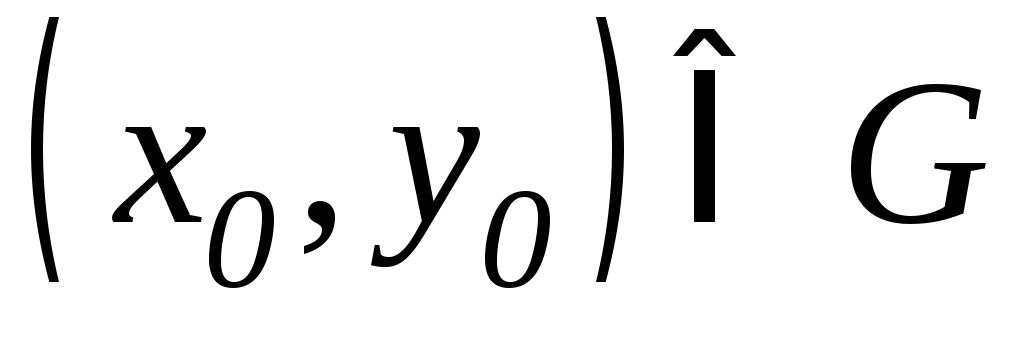 ,
существует единственное значение
постоянной
,
существует единственное значение
постоянной такое, что функция
такое, что функция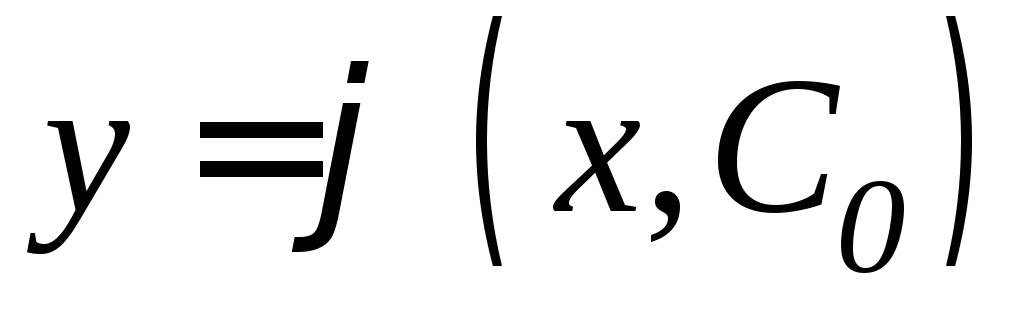 удовлетворяет данному начальному
условию
удовлетворяет данному начальному
условию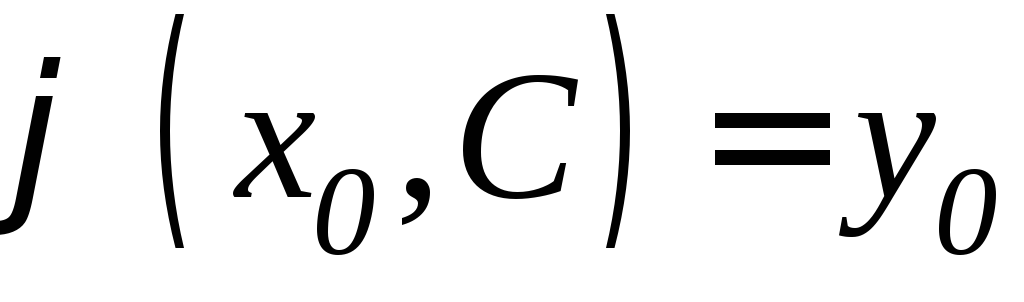 .
.
Частным решением
уравнения(11.1) в области![]() называется функция
называется функция![]() ,
которая получается из общего решения
,
которая получается из общего решения![]() при определенном значении постоянной
при определенном значении постоянной![]() .
.
Задача, в которой требуется найти частное решение уравнения (11.1), удовлетворяющее начальному условию (11.2), называется задачей Коши.
Пример 1.
Показать, что функция![]() удовлетворяет уравнению
удовлетворяет уравнению![]() .
.
Решение. Имеем
 .
.
Подставим
![]() и
и![]() в левую часть уравнения:
в левую часть уравнения:
 .
.
Получили тождество
![]() .
Следовательно, функция
.
Следовательно, функция![]() является решением данного уравнения.
является решением данного уравнения.
Пример 2.
Показать, что функция![]() служит решением дифференциального
уравнения второго порядка
служит решением дифференциального
уравнения второго порядка![]() .
.
Решение.
Находим![]() ,
,![]() .подставив
выражение для
.подставив
выражение для![]() и
и![]() в данное уравнение, получим
в данное уравнение, получим
![]() ,
,
т.е. функция
![]() действительно является решением данного
дифференциального уравнения.
действительно является решением данного
дифференциального уравнения.
Пример 3.
Проверить, что функция![]() ,
определяемая уравнением
,
определяемая уравнением![]() ,
является решением дифференциального
уравнения
,
является решением дифференциального
уравнения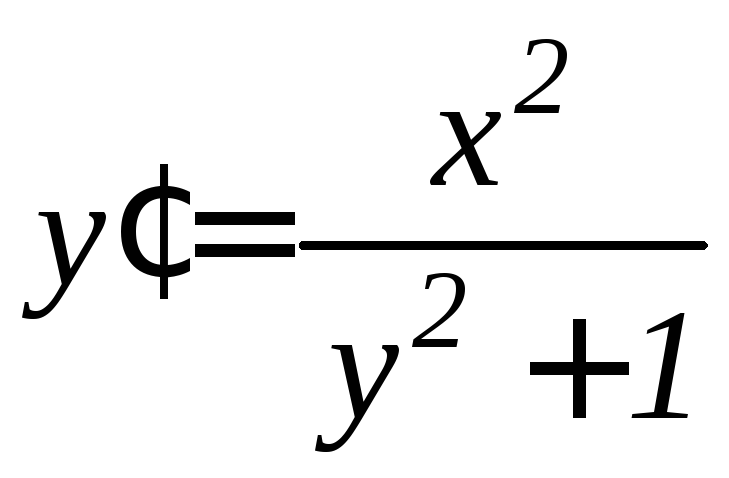 .
.
Решение.
Продифференцируем обе части
равенства![]() по переменной
по переменной![]() с учетом того, что
с учетом того, что![]() ;
тогда получим
;
тогда получим
![]() ,
или
,
или
![]() ,
откуда
,
откуда .
.
Пример 4.
Составить дифференциальное уравнение
семейства окружностей![]() .
.
Решение.
Дифференцируя данное выражение,
получаем![]() ,
откуда
,
откуда .
Исключаем теперь произвольную постоянную
.
Исключаем теперь произвольную постоянную![]() .
Для этого из последнего уравнения
находим
.
Для этого из последнего уравнения
находим![]() ,
подставляя его в данное уравнение,
получим
,
подставляя его в данное уравнение,
получим
![]() .
.
Это и есть дифференциальное уравнение данного семейства окружностей.
Дифференциальное уравнение вида
![]() ,
(11.3)
,
(11.3)
где
![]() ,
,![]() ,
,![]() ,
,![]() - непрерывные функции, называетсядифференциальным уравнением с
разделяющимися переменными.
- непрерывные функции, называетсядифференциальным уравнением с
разделяющимися переменными.
Если ни одна из
функций
![]() ,
,![]() ,
,![]() ,
,![]() тождественно не равна нулю, то в
результате деления уравнения (11.3) на
тождественно не равна нулю, то в
результате деления уравнения (11.3) на![]() оно приводится к виду
оно приводится к виду
 .
.
Почленное интегрирование этого уравнения приводит к соотношению
 ,
,
которое и определяет (в неявной форме) решение уравнения (11.3).
Пример 5. Найти общее решение уравнения

и выделить
интегральную кривую, проходящую через
точку
![]() .
.
Решение. Данное уравнение можно переписать в виде
 или
или
![]() .
.
Полученное уравнение
является уравнением с разделяющимися
переменными (коэффициент при
![]() - функция только от
- функция только от![]() ,
коэффициент при
,
коэффициент при![]() - функция только от
- функция только от![]() ).
).
Интегрируя, получим общее решение
 .
.
Полагая в нем
![]() ,
,![]() ,
находим
,
находим![]() .
Таким образом, частное решение, проходящее
через точку
.
Таким образом, частное решение, проходящее
через точку![]() -
-![]() .
.
Пример 6. Найти общее решение дифференциального уравнения
![]() .
.
Решение. Вынося общие множители за скобки, данное уравнение можно записать так:
![]() ,
,
откуда видно, что
это уравнение с разделяющимися
переменными. Разделив обе части последнего
уравнения на произведение
![]() ,
получим
,
получим
 .
.
Интегрируя это уравнение, находим
![]()
или
 ,
,
откуда получаем общее решение:
![]() .
.
Уравнение вида
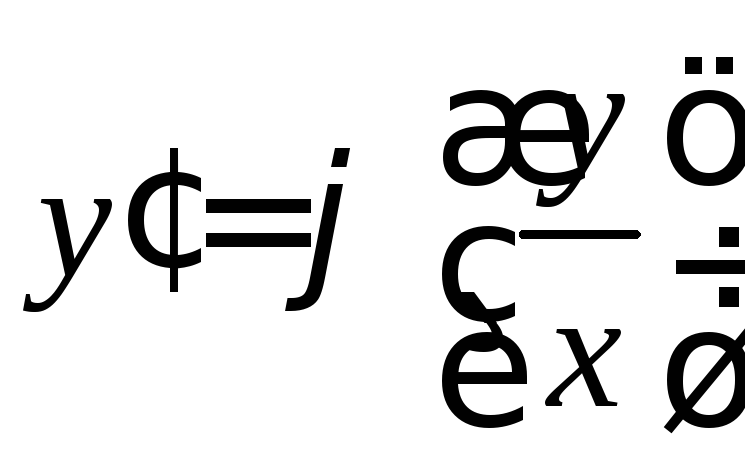 .
.
называется однородным.
С помощью подстановки
![]() ,
где
,
где![]() - новая неизвестная функция, оно
преобразуется к уравнению с разделяющимися
переменными.
- новая неизвестная функция, оно
преобразуется к уравнению с разделяющимися
переменными.
Уравнение
 ,
(11.4)
,
(11.4)
для которого
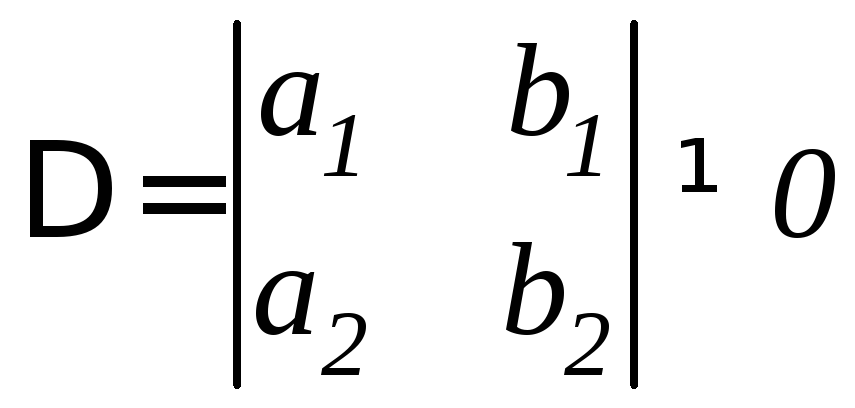
преобразованием

где постоянные
![]() и
и![]() находятся из системы уравнений
находятся из системы уравнений

сводится к однородному уравнению.
При
![]() преобразованием
преобразованием![]() уравнение (11.4) сводится к уравнению с
разделяющимися переменными.
уравнение (11.4) сводится к уравнению с
разделяющимися переменными.
Пример 7. Найти общее решение дифференциального уравнения
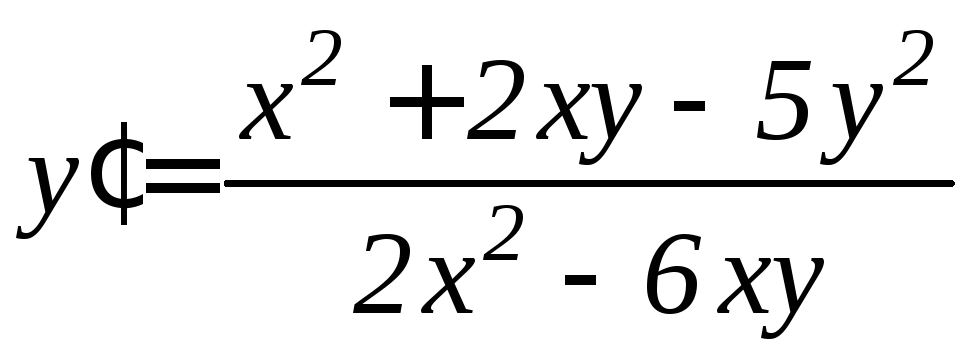 .
.
Решение.
Разделим числитель и знаменатель
правой части данного уравнения на![]() ,
получим:
,
получим:
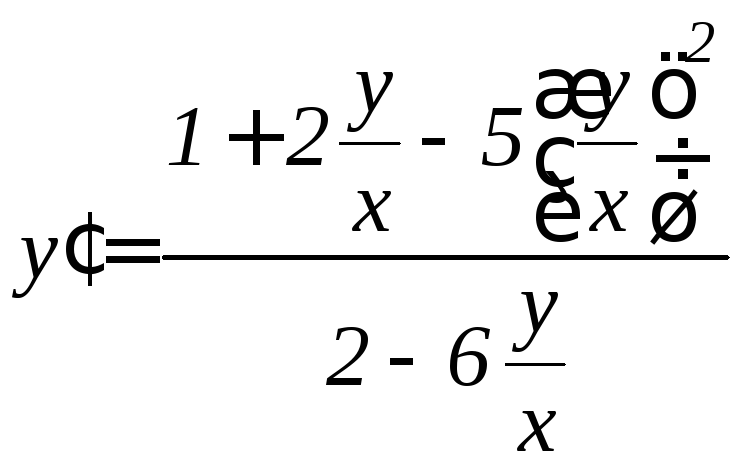 .
.
Делаем подстановку
![]() ,
где
,
где![]() - новая неизвестная функция. Тогда
- новая неизвестная функция. Тогда![]() и уравнение приводится к виду
и уравнение приводится к виду
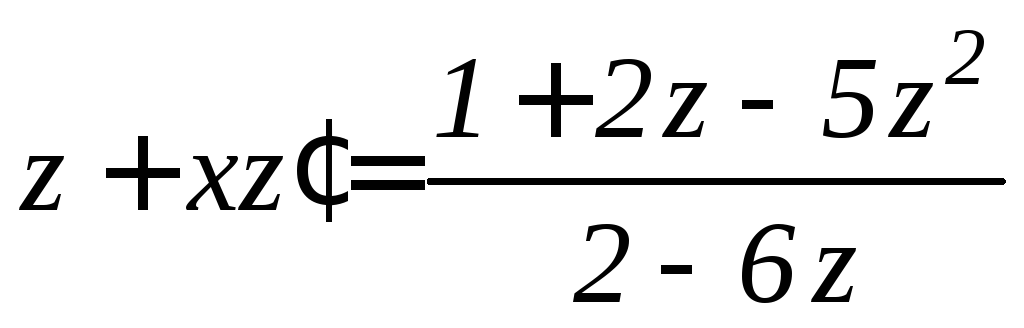 или
или
 .
.
Разделяем переменные:
![]() .
.
Интегрируя, получаем
2
arctg z - 3 ln(1+
z2)=
ln![]() +C.
+C.
Заменяя
![]() на
на![]() ,
получим общее решение данного уравнения:
,
получим общее решение данного уравнения:
 или
или
 .
.
Пример 8. Найти общее решение уравнения
![]() .
.
Решение. Это уравнение вида (11.4):
 ,
,
при этом
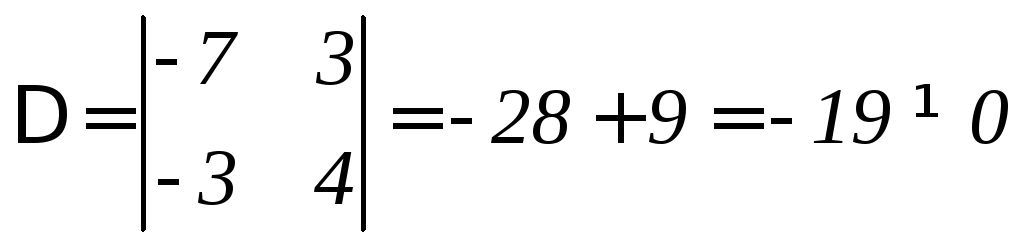 .
.
Вводим новые
переменные
![]() ,
,![]() ,
,
где
![]() и
и![]() должны удовлетворять системе уравнений
должны удовлетворять системе уравнений

Решая эти уравнения,
находим
![]() ,
,![]() .
.
Таким образом,
![]() ,
,![]() ;
;![]() ,
,![]() .
.
Исходное уравнение преобразуется к виду
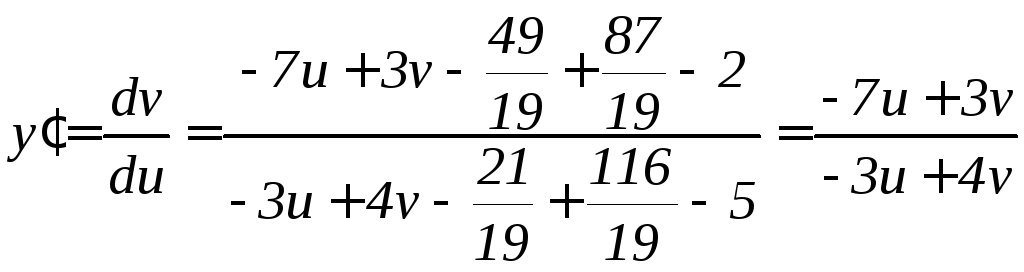
или
 .
.
В полученном
однородном уравнении положим
![]() ,
откуда
,
откуда![]() ;
приходим к уравнению с разделяющимися
переменными:
;
приходим к уравнению с разделяющимися
переменными:
![]() .
.
Преобразуем последнее уравнение:
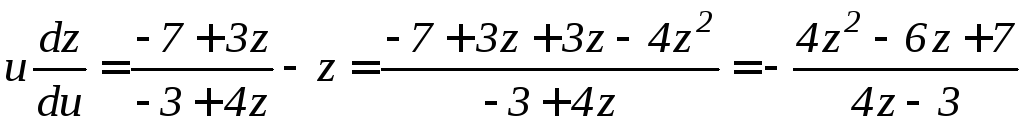 .
.
Разделяя переменные, получим
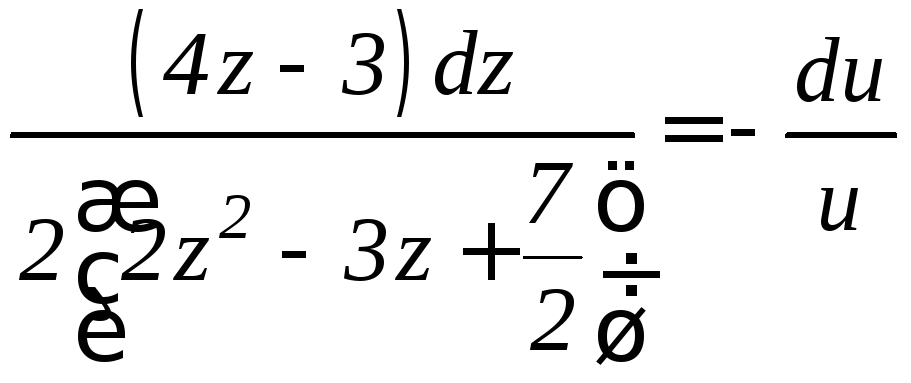 .
.
Пользуясь формулой
 ,
,
из последнего уравнения находим
 или
или
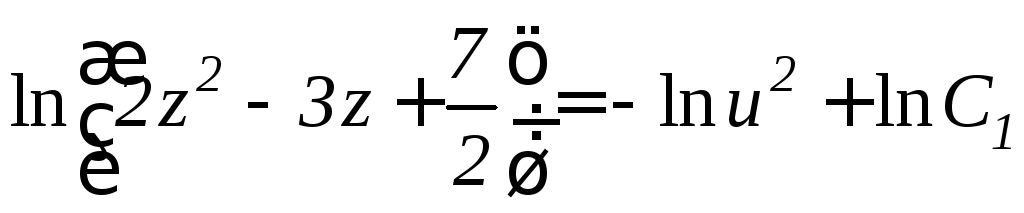 .
.
Отсюда
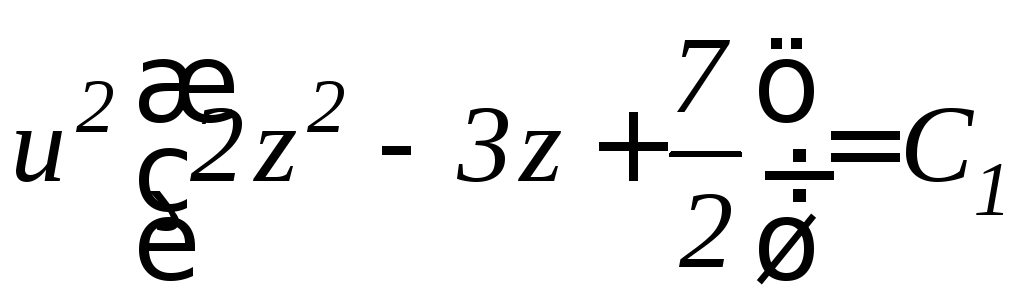 .
.
Подставляя сюда
![]() ,
получим
,
получим
 или
или
![]() .
.
Перейдем к переменным
![]() и
и![]() по формулам
по формулам![]() ,
,![]() :
:
 .
.
Раскрыв скобки и
заменив полученную в уравнении константу
на
![]() ,
получим общее решение исходного
уравнения:
,
получим общее решение исходного
уравнения:
![]() .
.
Уравнение вида
![]() ,
(11.5)
,
(11.5)
где
![]() и
и![]() - непрерывные функции, называетсялинейным дифференциальным уравнением
первого порядка(
- непрерывные функции, называетсялинейным дифференциальным уравнением
первого порядка(![]() и
и![]() входят в первых степенях, не перемножаясь
между собой).
входят в первых степенях, не перемножаясь
между собой).
Если
![]() ,
то уравнение (11.5) называется линейнымоднороднымуравнением. Если
,
то уравнение (11.5) называется линейнымоднороднымуравнением. Если![]() ,
то уравнение (11.5) называется линейнымнеоднороднымуравнением.
,
то уравнение (11.5) называется линейнымнеоднороднымуравнением.
Общее решение линейного однородного уравнения (11.4) легко получается разделением переменных:
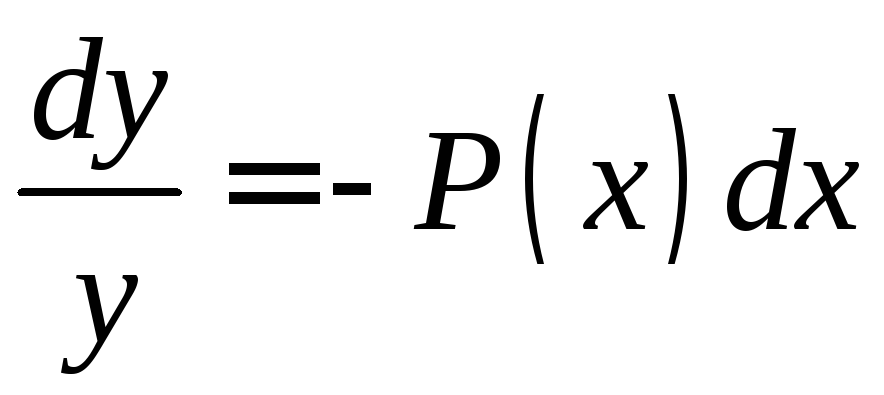 ;
;
 ;
;![]() ,
,
или, наконец,
![]() ,
,
где
![]() - произвольная постоянная.
- произвольная постоянная.
Решение линейного неоднородного уравнения ищется методом Бернуллив виде
![]() .
.
Подстановка
выражений для
![]() и
и![]() в уравнение (11.5) приводит его к виду
в уравнение (11.5) приводит его к виду
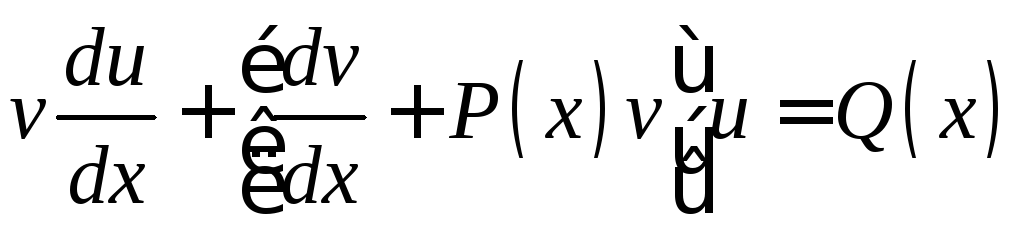 .
.
В качестве
![]() выбирают одну из функций, удовлетворяющих
уравнению
выбирают одну из функций, удовлетворяющих
уравнению
![]() ,
,
тогда функция
![]() определяется из уравнения
определяется из уравнения
![]() .
.
Общее решение линейного неоднородного уравнения можно найти исходя из общего решения соответствующего однородного уравнения методом Лагранжа или методом вариации постоянных, полагая
![]() ,
,
где
![]() - некоторая дифференцируемая функция
от
- некоторая дифференцируемая функция
от![]() .
.
Для нахождения
![]() нужно подставить
нужно подставить![]() в исходное уравнение (11.5), что приводит
к уравнению
в исходное уравнение (11.5), что приводит
к уравнению
![]() .
.
Отсюда
![]() ,
,
где
![]() - произвольная постоянная. Тогда искомое
общее решение линейного неоднородного
уравнения имеет вид
- произвольная постоянная. Тогда искомое
общее решение линейного неоднородного
уравнения имеет вид
![]() .
.
Уравнением Бернуллиназывается уравнение вида
![]() ,
(11.6)
,
(11.6)
где
![]() - действительное число. В случае
- действительное число. В случае![]() ,
,![]() уравнение (11.6) является линейным. Во
всех других случаях оно сводится к
линейному с помощью подстановки
уравнение (11.6) является линейным. Во
всех других случаях оно сводится к
линейному с помощью подстановки
![]() .
.
Пример 9. Найти общее решение уравнения
![]() .
.
Выделить решение,
удовлетворяющее условию
![]() .
.
Решение. Разделим переменные в данном уравнении:
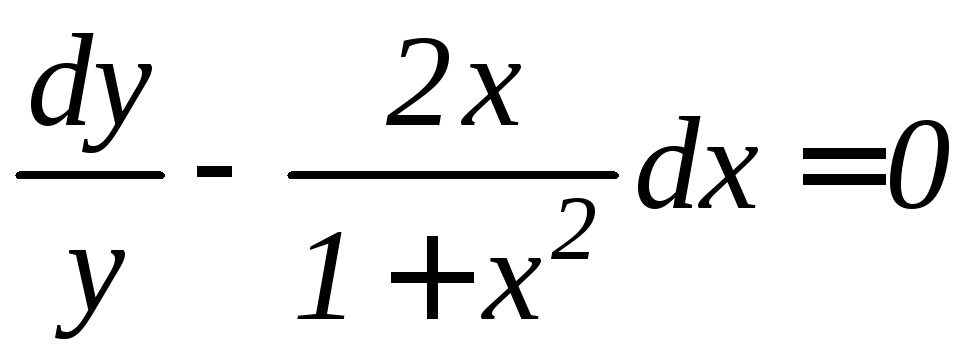 .
.
Интегрируя, получим
![]() или
или
![]() .
.
Решение, удовлетворяющее поставленному начальному условию, имеет вид
![]() ;
;
![]() ;
;![]() .
.
Пример 10. Решить уравнение
![]() .
.
Решение.
Разделив левую и правую части
данного уравнения на![]() ,
приходим к линейному неоднородному
уравнению:
,
приходим к линейному неоднородному
уравнению:
![]() .
.
Применим метод
Бернулли. Пусть
![]() ,
тогда
,
тогда![]() и уравнение примет вид
и уравнение примет вид
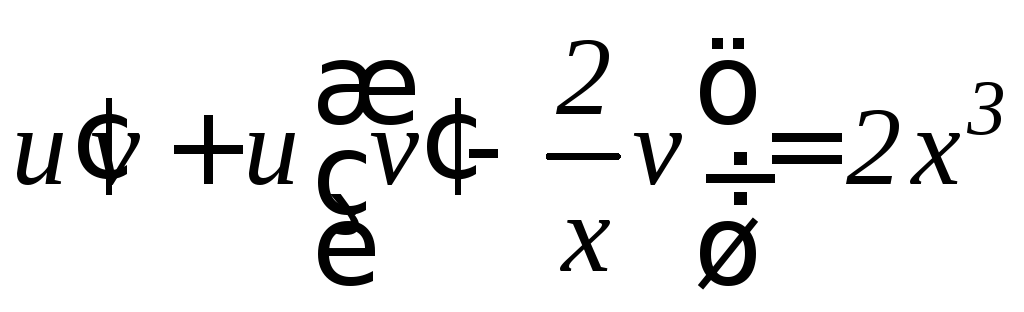 .
.
Положим
![]() или
или
![]() .
.
Проинтегрировав,
найдем какое-либо частное решение этого
уравнения, например, при
![]()
![]() и
и
![]() .
.
При этом данное уравнение обратится в уравнение
![]() или
или
![]() .
.
Решая это уравнение, получим
![]() .
.
Таким образом, окончательно имеем
![]() .
.
Пример 11. Решить уравнение
![]()
при начальном
условии
![]() .
.
Решение. Соответствующее однородное уравнение имеет вид
![]() .
.
Разделив переменные, получим
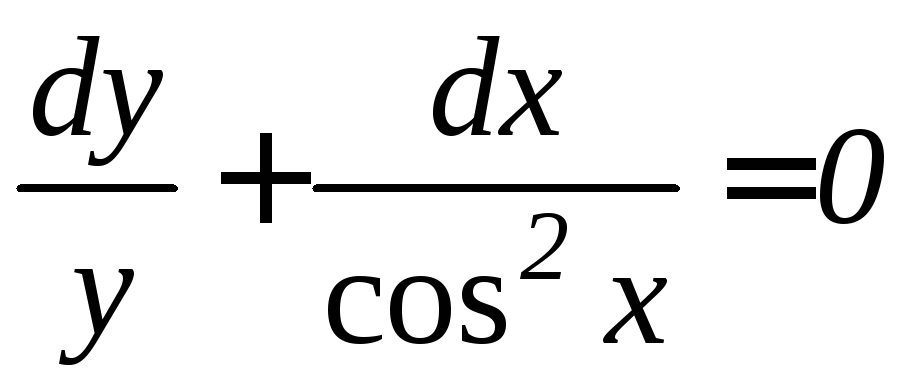 ,
,
![]() ,
,![]() .
.
Ищем решение исходного неоднородного уравнения в виде
![]() ,
,
где
![]() - неизвестная функция. Подставляя в
исходное уравнение
- неизвестная функция. Подставляя в
исходное уравнение![]() и
и![]() ,
придем к уравнению
,
придем к уравнению

или
![]()
откуда
 .
.
Интегрируя по
частям при
![]() ,
,![]() и
и![]() ,
,![]() ,
получим
,
получим
![]() .
.
Таким образом, получаем общее решение исходного уравнения
![]() .
.
Используя начальное
условие
![]() ,
получим
,
получим![]() ,
откуда
,
откуда![]() .
Следовательно, искомое решение задачи
Коши
.
Следовательно, искомое решение задачи
Коши![]() .
.
Пример 12. Найти общее решение уравнения
![]() .
.
Решение. Преобразовав уравнение к виду
![]() ,
,
убеждаемся, что
это уравнение Бернулли с
![]() .
С помощью подстановки
.
С помощью подстановки
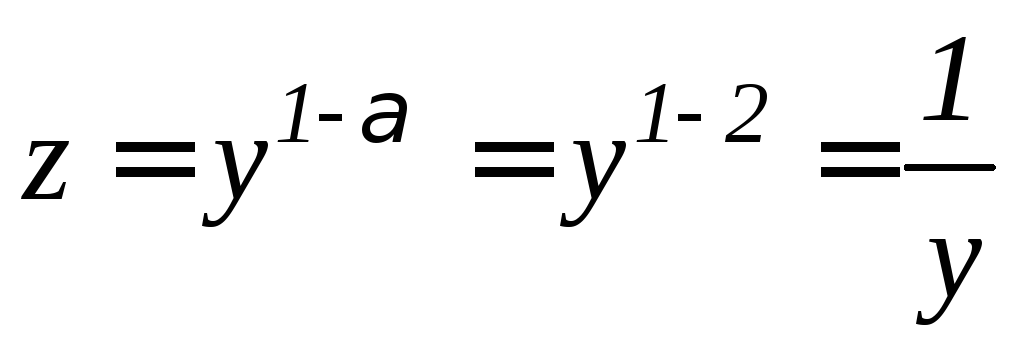 ,
,
![]() ,
,![]()
данное уравнение приводится к линейному
![]() .
.
Решая однородное уравнение
![]() ,
,
![]() ,
,![]() ,
,
получаем
![]() .
.
Ищем решение неоднородного уравнения в виде
![]() ,
,
![]() .
.
Подставляем в уравнение
![]() или
или
![]() .
.
Разделяя переменные и интегрируя, получаем
![]() ,
,
![]() .
.
Таким образом, общее решение неоднородного уравнения имеет вид
![]() ,
,
или, после замены
![]() ,
,
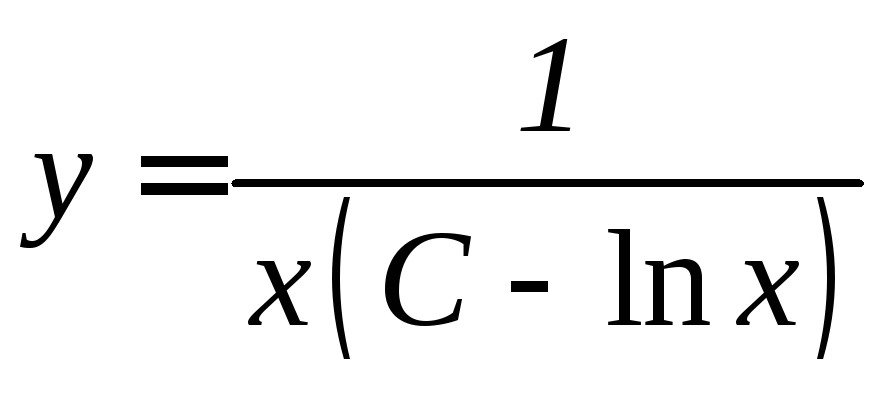 .
.
Уравнение вида
![]() ,
(11.7)
,
(11.7)
где левая часть
представляет полный дифференциал
некоторой функции
![]() в некоторой области
в некоторой области![]() ,
называетсяуравнением в полных
дифференциалах.
,
называетсяуравнением в полных
дифференциалах.
Его можно записать в виде
![]() ,
,
где
![]() - такая функция, что
- такая функция, что![]() .
Отсюда следует, что общее решение
уравнения (11.7) имеет вид
.
Отсюда следует, что общее решение
уравнения (11.7) имеет вид![]() .
Решение сводится к отысканию функции
.
Решение сводится к отысканию функции![]() .
.
Для того чтобы
уравнение (11.7) было уравнением в полных
дифференциалах, необходимо и достаточно,
чтобы во всех точках области
![]() ,
в которой функции
,
в которой функции![]() и
и![]() определены, непрерывны и имеют
непрерывные частные производные
определены, непрерывны и имеют
непрерывные частные производные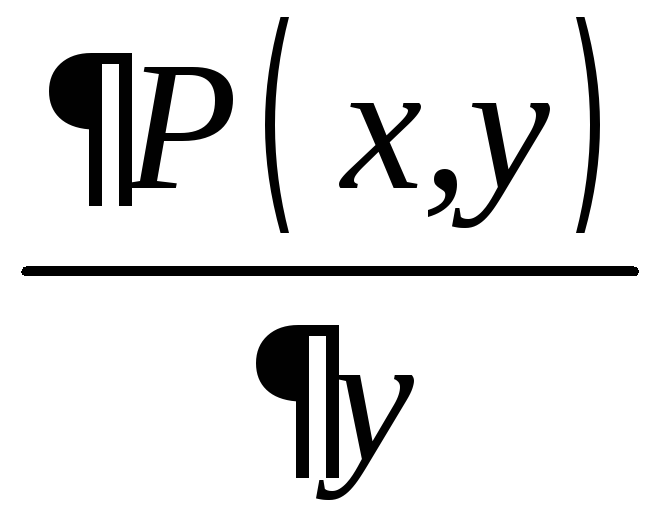 и
и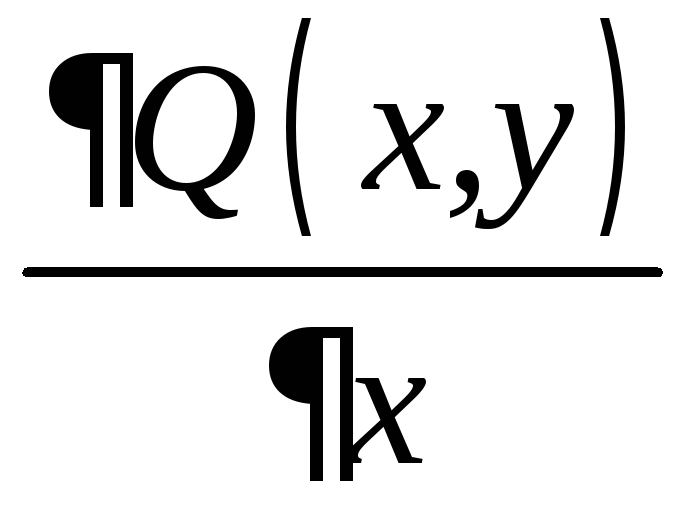 ,
было выполнено условие
,
было выполнено условие
 .
(11.8)
.
(11.8)
В том случае, когда условие (11.8) выполнено, общий интеграл уравнения (11.7) можно записать в виде
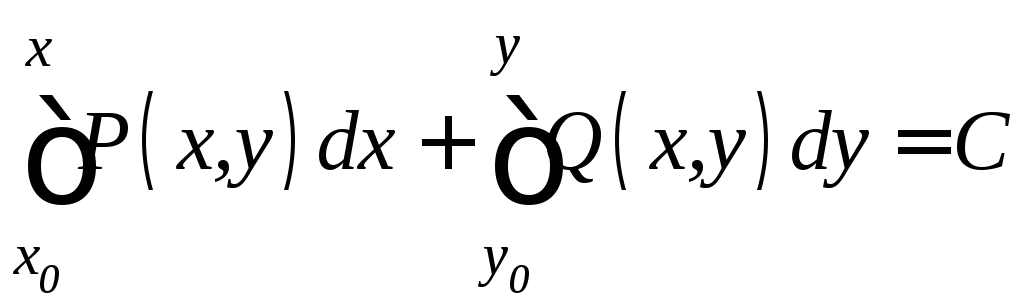
или
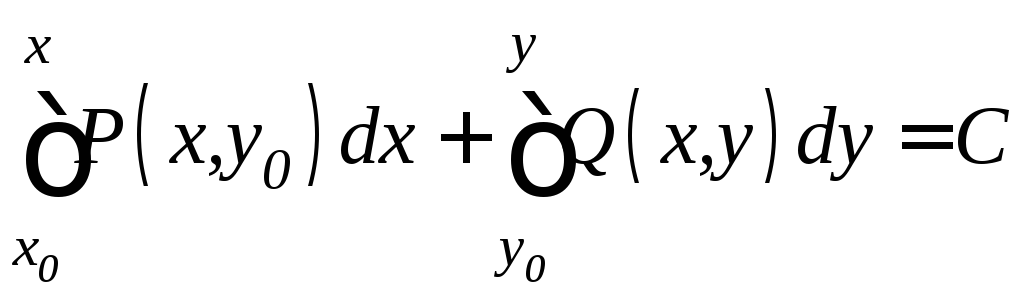 ,
(11.9)
,
(11.9)
где
![]() - произвольная фиксированная точка
области
- произвольная фиксированная точка
области![]() .
.
Если условие (11.8)
не выполнено, то уравнение (11.7) не является
уравнением в полных дифференциалах.
Однако в некоторых случаях его можно
привести к уравнению в полных дифференциалах
умножением на функцию
![]() ,
которая называетсяинтегрирующим
множителем.
,
которая называетсяинтегрирующим
множителем.
Интегрирующий
множитель легко находится, когда он
зависит только от
![]() ,
т.е.
,
т.е.![]() ,
или только от
,
или только от![]() ,
т.е.
,
т.е.![]() .
Первый из этих случаев имеет место,
если соотношение
.
Первый из этих случаев имеет место,
если соотношение

является функцией
только от
![]() ;
тогда интегрирующий множитель находится
по формуле
;
тогда интегрирующий множитель находится
по формуле
![]() (11.10)
(11.10)
Второй случай имеет место, если соотношение
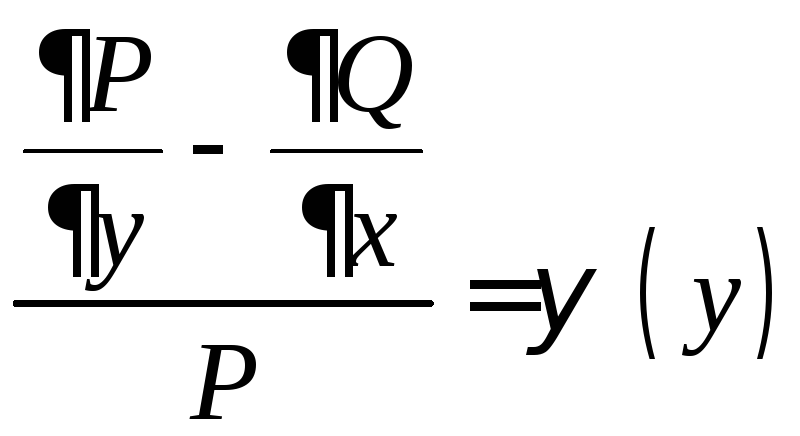
является функцией
только от
![]() ;
тогда интегрирующий множитель находится
по формуле
;
тогда интегрирующий множитель находится
по формуле
![]() .
(11.11)
.
(11.11)
Пример 13. Найти общее решение уравнения
![]() .
.
Решение. Здесь![]() ,
,![]() ,
, ,
,![]() ;
таким образом, условие (11.8) выполнено,
т.е. данное уравнение является уравнением
в полных дифференциалах.
;
таким образом, условие (11.8) выполнено,
т.е. данное уравнение является уравнением
в полных дифференциалах.
Найдем общее
решение по формуле (11.9), взяв
![]() ,
,![]() :
:
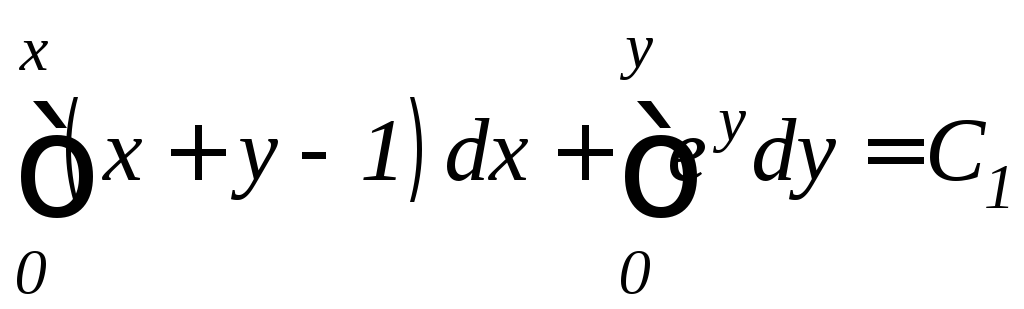 или
или
 .
.
Подставляя пределы, находим
 или
или
 ,
,
где
![]() .
.
Пример 14. Найти общее решение уравнения
![]() .
.
Решение. Здесь
![]() ,
,![]() ,
так что
,
так что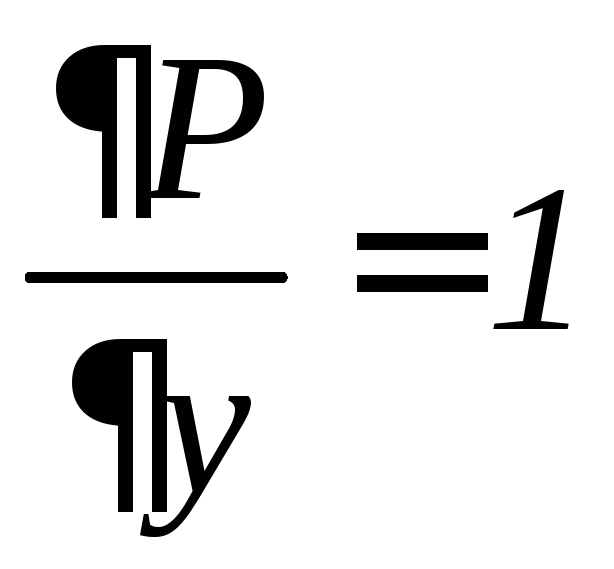 ,
,![]() ,
т.е. условие (11.8) не выполняется. Проверим,
существует ли дляданного
уравнения интегрирующий множитель.
Поскольку
,
т.е. условие (11.8) не выполняется. Проверим,
существует ли дляданного
уравнения интегрирующий множитель.
Поскольку
 ,
,
то интегрирующий множитель вычисляется по формуле (11.10):
 .
.
Умножив обе части
исходного уравнения на
![]() ,
получаем уравнение
,
получаем уравнение
![]() ,
,
которое, как нетрудно проверить, является уравнением в полных дифференциалах.
Решим это уравнение.
Полагая
![]() ,
,![]() и используя формулу (11.9), имеем
и используя формулу (11.9), имеем
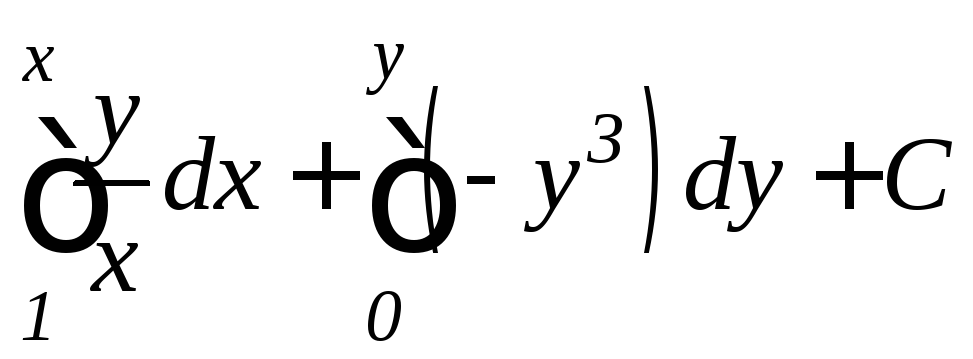 ,
,
т.е.
 или
или
 .
.
Это и есть общее решение данного уравнения.
