Как получить допуск к выполнению лабораторной работы

Чтобы приступить к выполнению лабораторной работы, предварительно нужно получить у преподавателя допуск, для чего необходимо во внеурочное время:

1. Внимательно прочитать методические указания к работе.

2. Изучить теоретический материал, необходимый для усвоения знаний по работе. При необходимости изучить дополнительную литературу (список литературных источников прилагается).

3. На листах формата А-4 аккуратно написать от руки (можно набрать на компьютере): цель и задачи работы; содержание; оборудование, технические и инструментальные средства; порядок выполнения работы; таблицу для записи результатов измерения; формулы для расчетов.

4. При подготовке к занятию ознакомиться с лабораторной установкой, выяснить для себя, что и как измерять.

5. Во время аудиторного лабораторного занятия получить допуск к работе у преподавателя.

Как оформить лабораторную работу

1. Титульный лист: Министерство образования и науки РК, ЮКГУ им. М.Ауезова, кафедра «Физика», название и номер лабораторной работы, ФИО студента, группа, ФИО преподавателя, город, год.

2. Начиная со второго листа, аккуратно, без грамматических ошибок, пишутся от руки (можно набрать на компьютере): цель и задачи работы; содержание; оборудование, технические и инструментальные средства; порядок выполнения работы; таблица с результатами измерения; формулы; расчеты; контрольные вопросы и ответы на них.

3. Ксерокс, сканирование текста методических указаний не допускаются.

4. Если в работе нужно строить графики, то их необходимо чертить на миллиметровой бумаге.

Защита и оценка выполненной лабораторной работы

Чтобы защитить выполненную лабораторную работу, нужно представить преподавателю письменный и устный отчет по работе. Максимальный балл (см. силлабус) за лабораторную работу выставляется студенту, если:

1. Студент выполнил работу в полном объеме.

2. Студент знает название, цель и задачи, содержание, порядок выполнения работы.

3. Студент знает оборудование, технические и инструментальные средства, используемые в работе, а также на лабораторной установке может показать, как он выполнял работу, что и как измерял.

4. Студент может написать и объяснить используемые в работе формулы и прокомментировать свои расчеты.

5. Студент дает полные и правильные ответы на контрольные вопросы.

Минимальный балл (см. силлабус) за лабораторную работу выставляется студенту, если он выполнил работу в полном объеме, правильно ее оформил, но во время защиты предоставил только письменный отчет.

Лабораторная работа № 1. Математическая обработка результатов прямых измерений

Цели и задачи работы: ознакомление с методикой обработки результатов многократных прямых измерениий на примере обработки данных измерениий периода колебаний математического маятника, определение наиболее вероятного значения измеряемой величины, стандартного отклонения, доверительного интервала при заданной надежности

Содержание работы: Измерения делятся на прямые и косвенные Прямые измерения производятся с помощью приборов, которые измеряют саму исследуемую величину Так, массу тел можно найти с помощью весов, длину – измерить линейкой, а время – секундомером Измерения плотности тела по их массе и объему, скорости поезда – по величине пути, пройденного за известное время, принадлежат к косвенным измерениям

Любое измерение из-за несовершенства органов чувств человека и измерительных приборов сопряжно с погрешностями. При любых измерениях допускаются некоторые ошибки, поэтому результаты измерений дают нам не истинное, а лишь приближенное значение измеряемой величины Установление допускаемой погрешности измерения, интервала, в котором лежит истинное значение измеряемой величины, является необходимым условием надежности эксперимента Погрешности измерений делят на промахи, а также систематические и случайные погрешности

Промахи возникают вследствие неисправности прибора или невнимательности наблюдателя, при нарушении методики эксперимента или условий его проведения В большенстве случаев промахи хорошо заметны, так как соответствущие им отсчеты резко отличаются от подобных отсчетов Результат измерения, содержащего промах, не должен учитываться при обработке данных – его следует просто отбросить

Систематические погрешности возникают вследствие неисправности или неточности градуировки измерительных приборов, при использовании для расчетов неточных данных, а также вследствие несовершенства самого метода измерения Эти ошибки влияют на результаты измерения всегда односторонне Очевидно, что влияние систематических ошибок нельзя снизить увеличением числа измерений Однако, если природа и характер систематических ошибок известны, влияние их на результат измерения можно учесть введением поправок и исключить.

Случайные ошибки обусловлены флуктуациями измеряемой величины, появление их не может быть предупреждено, поэтому они могут оказать определенное влияние на отдельные измерения, изменяя результат в обе стороны, то есть и увеличивать и уменьшать их Они подчиняются статистическим законам, поэтому влияние случайных ошибок на результат измерений можно учесть или значительно уменьшить Применяя законы теории вероятности, определяются наиболее вероятные значения измеряемых величин и возможные отклонения от этих значений.

Пусть при многократном измерении некоторой физической величины было полученоее значений:Тогда среднее арифметическое из всех полученных значений, которое является наиболее достоверным, равно:

(1.1.1.)

Каждое отдельное измерение отличаются от среднего арифметического на величину, равную

(1.1.2.)

Отклонение называется абслютной погрешностьюі–того измерения Абсолютные погрешности принимают как положительные, так и отрицательные значения

Из опыта известно: чем больше ошибка, тем вероятность ее проявления меньше Кроме того, если число измерений очень велико, то ошибки, одинаковые по величине, но разные по знаку, встречаются одинаково часто Быстрота уменьшения вероятности появления погрешности с ее увеличением характеризуется дисперсией:

(1.1.3)

Чем меньше дисперсия, тем меньше вероятность появления большей по величине случайной ошибки и меньше разброс отдельных значений

(1.1.4)

Следовательно,

(1.1.5)

Корень квадратный из дисперсии измеренний называется средней квадратичной ошибкой

(1.1.6)

Если вместо в выражении (1.1.6) подставитьего значение из (1.1.2), то

(1.1.7)

В выражение (1.1.7) входит величина , которая определена с какой-то ошибкой Средней квадратичной ошибкой среднего арифметического ряда измерений называется величина, равная средней квадратной из числа измерений

(1.1.8)

или

(1.1.9)

Оценки дисперсии иявляются предельными, справедливыми лишь при больших При малых значения эти оценки, сами являющиеся случайными, в лучшем случае определяют лишь порядок величины дисперсии

Задача обработки измерений заключается в определений интервала от до+, в котором с вероятностьюзаключено истинное значение измеряемой величины Интервал от доназывается доверительным интервалом, аназывается доверительной вероятностью (илинадежностью)

Если число измерений достаточно велико, то доверительная вероятность выражает долю из общего числа измерений, в которых измеряемая величина оказывается в пределах доверительного интервала Например, если сделано 100 измерений, то при доверительной вероятности в 95 измерениях были получены значения, не выходящие за его пределы Чем большая надежность требуется, тем больше получается соответствующий доверительный интервал.

Из теории ошибок следует, что при большом числе измерений (больше ста опытов) доверительная вероятность интервала от доравна 68%, а интервала отдоравна 95%. При представлении любого измеренного значения главное – это привести интервал и доверительную вероятность, соответствующей этому интервалу.

В тех случаях, когда число измерений невелико, отсутствуют условия для строгого проявления статистических закономерностей, которые лежат в основе определения случайных погрешностей Это приводит к тому, что значение среднеквадратичного отклонения от среднего S_a , вычисленное по формуле (1.1.9), неточно, и неточность тем больше, чем меньше число измерений.

Следовательно, чтобы гаранатировать, что истинное значение измеряемой величины с заданной вероятностью находится в пределах доверительного интервала, последний приходится увеличивать При ограниченном числе измерений за границу доверительного интервала принимается не S_a, а следующее значение:

(1.1.10)

Численное значение зависит от величины доверительной вероятности и числа измерений. Оно называется коэффициентом Стьюдента Результат измерения

(1.1.11)

Результаты измеренияй разнородных величин нельзя сравнивать друг с другом по их абсолютным ошибкам Для сравнения точности измерений таких величин вводится относительная ошибка – отношение абсолютной ошибки к среднему значению измеряемой величины

(1.1.12)

По относительной погрешности удобно сравнивать результаты измерений однородных величин

Оборудование: математический маятник, секундомер.

Порядок выполнения работы:

1. Измерить время 20-30 колебаний маятника (количество колебаний маятника N задается преподавателем) Измерения повторить n раз (количество опытов n задается преподавателем)

2. Для каждого опыта найти период колебаний маятника по формуле:

3. Определить среднее арифметическое значение периода колебаний маятника по формуле:

4. Найти для каждого опыта величину

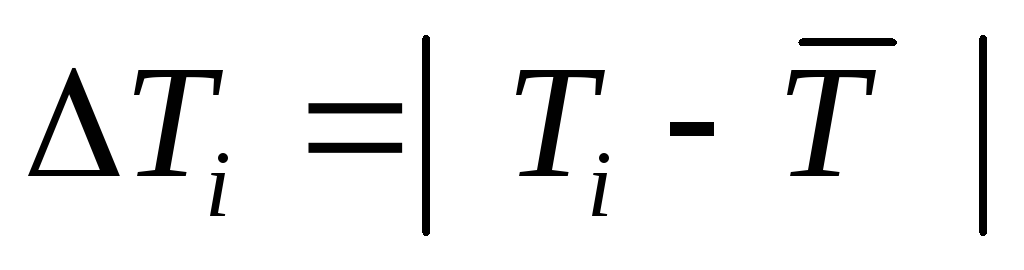
5. Возвести в квадрат, сложить полученные значения.

6. Найти стандартное отклонение периода колебаний по формуле:

7. По таблице, имеющейся в лаборатории, найти значение коэффициента Стьюдента, соответствующее надежности, указанной преподавателем, и числу опытов.

8. Вчислить абсолютную ошибку измерений по формуле:

9. Рассчитать относительную ошибку по формуле

10. Результаты измерений и вычислений занести в таблицу:

N	n	ti , с	Тi, с	, с	, с2	,с2	, с		, с	, %
	1
	2
	…

Контрольные вопросы:

1. На какие виды делятся измерения?

2. На какие виды делятся погрешности

3. Как определяется абсолютная ошибка измерений

4. Что такое коэффициент Стьюдента

5. Как влияет коэффициент Стьюдента на результат измерений?

6. Что такое доверительный интервал?

7. Что такое доверительная вероятность

8. Что такое относительная погрешность

9. Почему необходимо вычислять относительную погрешность?

10. Что называется математическим маятником и периодом его колебаний

Литература:

1. Исатаев С.И., Аскарова А.С., Бердибаев М.С. и др. Лабораторный практикум по механике. – Алматы: РИК, 2000.

2. Сулеева Л.Б., Полякова Л.М., Спицын А.А., Бегимов Т.Б., Джумабаев Р.Н. Механика и молекулярная физика. Физический практикум. – Алматы: Мектеп, 2003.

3. Трофимова Т.И. Курс физики: Учебное пособие для инженеров технических специальностей ВУЗов. Изд. 6-е/7-е. - М.: Высшая школа, 1999.