Системы нулевого порядка

Дифференциальное уравнение, описывающее систему нулевого порядка, является лишь простым алгебраическим уравнением. Система является ста­тической или, говоря другими словами, частотно-независимой. Примером системы нулевого порядка служит потенциометрический преобразователь смещения, изображенный на рис. 2.38(а). В этом датчике смещение х преоб­разуется в пропорциональное ему выходное напряжение V. Предположим, что сопротивление между нижним концом потенциометра и движком равно

R₀ при x = 0, а максимальное сопротивление при х = х_тax равно R_тax; тогда связь между выходным напряжением V и смещением х можно представить в виде

Это частный случаи уравнения вида:

y=ax+b

Здесь b либо имеет нулевое значение, либо играет роль начального сме­щения, аа — чувствительность. Время установленияt_s равно нулю, а шири­на полосы f0 равна бесконечности. В действительности, конечно, на очень высоких частотах чувствительность уменьшается, и у этого много причин (упругость, масса, паразитная емкость и т. д ); поэтому часто говорят, что такие системы являютсясистемами квази-нулевого порядка.Это означает, что реакция таких систем является мгновенной в том диапазоне частот, который существенен при измерении данной величины. Систему, изобра­женную на рис. 2.38(b), также можно считать системой нулевого порядка. Выходное напряжение датчика ХоллаV_H пропорционально токуI_H, проте­кающему по пластине Холла и индукцииВ магнитного поля, образуемого центральным проводником.

Кроме того, будет иметь место начальное сме­щение V₀. В разделе 3.2.3 будет показано, что

Рис 2 38 Системы нулевого порядка (а) потенциометрический преобразова­тель смещения и (b) датчик тока.

Здесь R_H — постоянная Холла для данной пластины, аt— ее толщинаПоскольку значение В пропорционально току, текущему по центральному проводнику, такой датчик исключительно удобен для измерения больших токов. Он позволяет осуществить такое измерение, не разрывая проводник для подключения пробника, который внес бы дополнительное сопротивле­ние.

Системы первого порядка

Улинейных систем первого порядка соотношение между входным сигналомх(t) и выходным сигналомy(t) выражается линейным дифференциальнымуравнением первого порядка. Простой пример такой системы — ртутный термометр. Изменение длины столбика ртути, определяемое по откалиброванной шкале, служит выходным сигналом, а входным сигналом является измеряемая температура окружающей среды Тi. Мы будем предполагать, что изменение длины столбика ртути прямо пропорционально изменению тем­пературы ртути в резервуаре термометра. Поэтому для описания динамичес­кого поведения термометра вполне можно принять температуру Т₀ ртути в резервуаре за выходную величину (см рис. 2.39(а)). Теплообмен между ртутью в резервуаре и окружающим воздухом должен происходить через стеклян­ную стенку с тепловым сопротивлениемR. Тепловую емкость (теплоемкость)ртути в резервуаре обозначим С. Для малого приращения тепла ΔQ получим:

Кроме того,

Поэтому

Другой пример системы первого порядка — это RС-цепь, приведенная на рис. 2.39(b). Пусть Vi и V₀ — входное и выходное напряжения. С учетом того, что

и

Рис. 2.39. Два примера систем первого порядка: (а) ртутный термометр и (b) RC – цепь.

Находим:

Полагая в обоих случаях RC =τ, мы можем представить эти линейные дифференциальные уравнения первого порядка в следующем общем виде:

где х = х(t), а у = y(t) Таким образом, мы можем придти к выводу, что ртутный термометр и R С- цепь эквивалентны с точки зрения их динамичес­кого поведения. Это дифференциальное уравнение решается просто. При скачкообразном входном сигнале

x(t)=x₀

при t > О

и x(t)=0

при t <0

а выходной сигнал у(t), или переходную характеристику, находим из

В операторной форме уравнение имеет вид:

Откуда

Общее решение таково: у = С.

Частным решением при t → ∞ является функция y(t) = у₀ (конечноеили установившееся значение):

Полагая, что у(t) = 0 при t = 0, найдем:

Таким образом,переходная характеристика измерительной системы пер­вого порядка имеет вид

где у₀ - конечное или установившееся значение, а τ =RC- постояннаявремени. Эта переходная характеристика изображена на рис.2.40.

Если относительная погрешность измерительной системы не может пре­восходить  = Δy_о /y_о, то время установления t_s равно

t_s = -τ lпе

Это легко получить из выражения для переходной характеристики с по­мощью графика на рис. 2.40. Когда требуется очень малая относительнаяошибка Δy_о /y_о в конечном отсчете на выходе такой системы первого поряд­ка,ее время установленияt_s становится чрезмерно большим. В примере с термометром на рис. 2.39(а) столбик ртути все медленнее ползет вверх к конечной отметке, которая достигается только при наступлении тепловогоравновесия между системой и ее окружением. Это является нежелательным свойством отклика первого порядка, когда речь идет о точных измерениях; время установления будет слишком большим.

Частотная характеристика — это, по существу, отклик системы на си­нусоидальный входной сигналx(t)= xsin(wt)вустановившемся режиме, тоесть отклик, спустя длительное время после включения сигнала и подачи его на вход, когда все переходные явления затухнут. Частотную характерис­тику находят как частное решение дифференциального уравнения, описы­вающего систему первого порядка, приt → ∞ .

Частотную характеристику легко получить, применяя комплексные пе­ременные в электрическом аналоге системы первого порядка, приведенном на рис.2.39.(b). Это даёт:

(при  =RC )

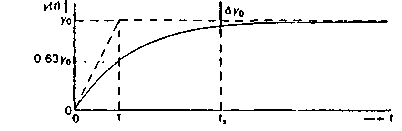
Рис 2 40. Переходная характеристика системы первого порядка.

Модуль S(w) равен

a аргумент S(w) имеет вид:

Arg S(w) = -arctg w .

Амплитудно-частотная характеристика S(w) и фазо-частотная характе­ристикаArg S(w) системы первого порядка представлены на рис241. Ширина полосы f₀ системы первого порядка определяется из равенстпа w= 1, так чтоf₀ = 1 / 2π. На этой частоте сдвиг по фазе уже достигает значения -.π/4 или -45˚. На более высоких частотах сдвиг по фазе стремит­ся к -90°, тогда как амплитуда выходного сигнала уменьшается почти до нуля.

Рис. 2.41. Частотная характеристика системы первого порядка.

Системы второго порядка

В качестве примера системы второго порядка мы воспользуемся конструк­цией стрелочного прибора (в частности, измерителя с подвижной катуш­кой), которая представляет собой вращающуюся механическую систему Каждая из следующих четырех механических пар сил оказывает воздействие на вращающуюся часть измерителя, создавая вращающий момент рис 2.42(а):

• Отклоняющее воздействие. Это воздействие вызывает отклонение стрел­ ки на уголθ. Момент этого воздействия пропорционален измеряемой вели­ чине (току). Мы обозначим этот моментM_d

Рис 2 42 Системы второго порядка: (а) механическое вращение; (b) механи­ческое поступательное движение; (с) параллельный электрический контур.

- Возвращающее воздействие. Это воздействие оказывает противодействие отклонению стрелки. В данном примере оно создается спиральной пружи­ной; вращающий момент этого воздействия обозначается М_r. Когда достига­ется установившееся состояние, отклоняющий момент и возвращающий момент равны:М_d=М_r Обычно бывает так, что возвращающий моментпропорционален углу отклонения θ, то есть М_r = К_r θ, где К_r — коэффициент упругости (жесткость пружины).

- Демпфирующее воздействие. Это воздействие также противодействует отклоняющему моменту. Демпфирующий момент пропорционален угловой скорости стрелки, так чтоМ_da=D_r dθ / dt. ЗдесьD_r — постоянная затуханиявращающейся конструкции. Затухание линейно зависит от угловой скорости dθ / dt.

Демпфирование применяют для того, чтобы предотвратить проскакивание стрелки за конечное значение и колебания стрелки вокруг него. Для этого используют те или иные крыльчатые приспособления и поршни (воз­душное демпфирование), а также индукцию вихревых токов в металличес­кой пластине в случае движущихся систем (демпфирование за счет токов Фуко).

Инерционность. Инерция вращающейся конструкции измерителя при­водит к возникновению еще одного противодействующего момента, кото­рый пропорционален угловому ускорению стрелки, так что

где J — момент инерции вращающейся конструкции относительно оси вращения.

Динамическое поведение измерителя определяется его уравнением дви­жения; в любой момент времени отклоняющий момент уравновешивается суммой всех других моментов:

М_i + M_da + M_r = M_d,

Или

В результате, как и следовало ожидать, мы пришли к линейному диффе­ренциальному уравнению второго порядка.

Чтобы сделать более ясной аналогию с другими системами, указанными на рис. 2.42, перепишем полученное уравнение, введя новую переменную w = d /dt:

Отклоняющий момент M_d является I-величиной (см приложение А 4), а угловая скоростьw — V-величиной. Вращающаяся механическая системааналогична системе с поступательным движением, изображенной на рис 2.42(b). Эта последняя состоит из груза массы т, пружины с коэффициен­том упругостиK_t и демпфера с постоянной затуханияD_t Если на систему действует силаF_d то скоростьvгруза по отношению к земле удовлетворяет равенству

Поскольку v=dx/dt , мы снова приходим к тому же самому линейномудифференциальному уравнению второго порядка, что и полученное ранее. Наконец, обе механические системы — с вращательным и с поступатель­ным движениями — аналогичны электрической системе, показанной на рис. 2.42(с). На этот параллельный электрический контур действуетI-величина:по нему течет ток I_d Мы хотим определить V-величину, являющуюся реше­нием уравнения:

Это уравнение эквивалентно обоим уравнениям, полученным выше Все различие может состоять в том, что I-величины и V-величины поменяются местами. Структура системы остается одной и той же, когда мы переходим от J кт илиС, одновременно заменяяD_r наD_t или 1 /R, а такжеК_r - наК_t, или 1 / L (см. приложение А. 4). Принимая во внимание, что

последнее уравнение можно переписать в виде:

где Iпредставляет собой ток, текущий по катушкеL

Мы видим теперь, что дифференциальное уравнение, описывающее ли­нейную систему второго порядка, в общем случае содержит две постоянные а и b:

Здесь х — это величина входного воздействия х(t), а у — выходная вели­чинау(t), нормализованная по отношению к чувствительности по постоян­ному токуS(0), так чтоу=y(t)./S(0). Благодаря нормализации третья посто­янная в дифференциальном уравнении отсутствует. Чтобы сделать запись более наглядной, введем две другие постоянные: относительное затухание z и угловую частоту w₀ свободных незатухающих колебаний в системе, и пере­пишем общее уравнение с использованием этих констант:

В случае системы с вращением переменные и параметры, входящие в это уравнение, имеют вид:

а в случае системы с поступательным движением —

Для электрической цепи имеем

Соответствующее уравнение в операторной форме выглядит так:

И корни его равны

Необходимо различать следующие три характерных случая z< 1,z= 1 иz> 1.

Недостаточное демпфирование (z < 1)

Можно показать, что отклик системы y(t) на входной сигнал, имеющий форму скачка величины x₀, происходящего в момент t = 0, равен

где ;при выводе этого выражения предполагается, чтона­чальные значенияу(0) и (dy/dt)_t=oравны нулю. Конечное значение, достигаемое в установившемся режиме, равно

.

Непосредственно вслед за входным скачком возникают затухающие ко­ лебания с частотой w_i, наложенные на конечное значение (см рис. 2 43) Мы видим, что с ростомz затухание колебаний происходит все быстрее Поэто­му z называют относительной скоростью затухания. Если z = 0, то колебания в системе продолжаются и их частота равна w₀; система находится в режиме свободных колебаний. Таким образом, w₀ — это резонансная частота системы, в которой затухание отсутствует полностью

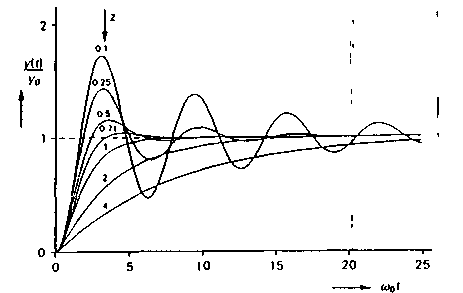
Рис.2.43. Переходные характеристики системы второго порядка при различных значениях относительного коэффициента z.

Критическое демпфирование (z = 1)

Предполагая снова, что начальные условия являются нулевыми, то есть у(0) = 0 и (dy/dt)_t=o= 0, а величина скачка на входе в моментt = 0 равна х₀, получаем следующее выражение для переходной характеристики системы второго порядка приz=1:

Как и ранее,конечное значение у₀ равно х₀, но теперь на выходе нет затухающих колебаний (см. рис 2 43).

Обычно измерители с подвижной катушкой бывают сконструированы таким образом, чтобы демпфирование у них было кг точно критическим, а слегка недостаточным (z= 1/) Из-за этого происходит небольшое проскакивание стрелки (4%) Достоинство такого подхода состоит в том, что наблюдатель яснее видит, когда стрелка устанавливается на конечном зна­чении.У такого значения коэффициента затухания z применительно к изме­рительным системам есть и другое достоинство: приz 0,7 амплитудно-частотная характеристика оказывается горизонтальной в возможно более широком диапазоне частот (этот вопрос рассмотрен ниже; см рис 2.45).

Избыточное демпфирование (z > 1)

При тех же начальных условиях, что и выше, но с коэффициентом зату­ханияz больше единицы, переходная характеристикаy(t) как реакция навходной скачок величины х₀ в момент t = 0 имеет вид:

где .В данном случае выходная величина будет постепенно приближаться («ползти») к конечному значению у₀ = х₀ (см. рис 2 43)

Постоянная времени прибора или его время установления (готовности) t_s зависит от коэффициента затухания z, периода T₀, соответствующего час­тоте свободных колебаний (T₀= 2/w₀), и, естественно, от допустимой относительной ошибки в конечной величинеу₀/у₀(см. рис. 2.44) У кривых на этом графике имеются разрывы приz< 1, обусловленные тем, что призаданных значениях T₀ и относительной погрешности (скажем 0,1%) время готовности t_s увеличивается скачками при непрерывном уменьшении коэф­фициента затухания z. Причина скачков заключается в том, что время готов­ности каждый раз увеличивается на один период затухающих колебаний

Частотную характеристику системы второго порядка легко найти, рас­сматриваяRLC -аналог такой системы, показанный; на рис 2 42(с):

Амплитудно-частотная характеристика имеет вид:

Рис. 2. 44. Время установления (готовности) t_s системы второго порядка при различных значениях допустимой относительной ошибки у₀ / у₀ в конечном результате у_а Т_а — период свободных колебаний, а z — относительный коэффициент затухания системы.

а для фазовой характеристики справедливо соотношение:

Подставляя z² =L/4R²C иw= 1/LC , можно написать эти выражения вобщей форме. Дифференцируя по w, находим, что максимум достигается прии значение в максимуме равно

(при z≤)

Частотная характеристика оказывается плоской в возможно более широ­ком диапазоне частот, если,то естьв случае, когдаz=. При этом ширина полосы системы равнаf₀=w₀/2π, гдеtw₀—частота свободных колебаний. В точке w = w₀ фазовый сдвиг равен —90°. На очень высоких частотах сдвиг по фазе стремится к —180°, но никогда непревышает этого значения, а величина сигнала на выходе системы приэтом почти равна нулю Если z < , то амплитудно-частотная характеристика имеет пик на частоте затухающих колебании (см рис.2 45 (а) и (b)).

Рис. 2.45. (а) Амплитудно-частотная и (b) фазо-частотная характеристики си­стемы второго порядка при различных значениях коэффициента затухания z.

Нелинейные системы

До сих пор мы рассматривали отклик систем, предполагая, что они являют­ся линейными. Но что произойдет, если эти системы нелинейны? На рис. 2.32 уже было показано, что по мере того, как входные величины становятся достаточно большими, всякая реальная система, в конце концов, становит­ся нелинейной из-за насыщения, перегрузки или ограничения. Сейчас на простом механическом примере мы проиллюстрируем, что происходит при этом с откликом.

Рассмотрим классический метод определения механической силы с по­мощью пружинного измерителя, в котором сила F_d приложенная к внут­ренней пружине, преобразуется в пропорциональное изменениеlдлиныпружины. Пусть штифт или кольцо, с помощью которых усилие передается пружине, обладают определенной массой, а о пружине предполагается, чтоу нее есть некоторое затухание Тогда при малом входном воздействии, когда сила мала, и малом соответствующем изменении длины, можно воспользо­ваться аналогом, изображенным на рис. 2.42(b). Когда l мало, статическое поведение пружинного измерителя силы определяется законом Гука: F_d=K_tl,

K_tl, где K_t — жесткость пружины (ее коэффициент упругости) Динамическое поведение этой линейной системы уже рассмотрено: при малых нагрузкахпружинный измеритель силы является линейной системой второго порядка «пружина с грузом» с демпфированием.

Однако в случае, когда прикладываемая сила велика, сказанное переста­ет быть справедливым: система становится нелинейной. Нелинейность воз­никает из-за того, что с увеличением растяжения или сжатия внутренняя пружина измерителя постепенно становится более, жёсткой или мягкой. Жесткость пружины больше не является постоянной. На рис. 2.46(а) показаны зависимости, иллюстрирующие статическое поведение такой нелинейной пружины.

Чтобы описать поведение пружинного измерители силы более реалис­тично с учетом нелинейности, сделаем в линейном дифференциальном урав­нении второго порядка, относящемся к механической системе с поступа­тельным движением, подстановку:v=dl/dt. В результате получим:

и l = l(t).

Нелинейность возникает из-за четвертого слагаемого в левой части пер­вого из приведенных равенств. Предполагается, что нелинейность пружины симметрична (одинакова для растяжения и сжатия). Наличие нелинейности обусловлено тем, что степеньlотлична от 1. Если β > 0, то пружина стано­вится все более жесткой, по мере того, как она растягивается или сжимает­ся. Если β = 0, то пружина линейна, а если β < 0, то она становится всеменее упругой с ростом l. При очень малых значениях l система ведет себя как линейная система второго порядка, так как в этом случае βl³ < K_tl ипоэтому членом βl³, ответственным за нелинейность, можно пренебречь,

Рис.2.46. Нелинейная система «пружина с грузом». (а) Пружина, становящяася более жёсткой, β > 0; линейная пружина, становящаяся более мягкой β < 0; F_d – сила, необходимая для растяжения/сжатия пружины на величину l основной гармоники свободных колебаний нелинейной системы и нормированной резонансной частотой w/w_0.

Чтобы составить верное представление о динамическом поведении, рас­смотрим сначала свободные колебания системы:F_d(t) = 0 приt≥0.Крометого, предположим, что демпфирование отсутствует: D_t = 0. Однажды под­вергнутая воздействию, система будет продолжать колебаться, порождаяпериодическийсигналl = l(l) = l(t ±пТ), п — целое.Теперьпериод Т = 1/f=2π/w зависит отамплитуды колебаний! Это показано на рис. 2.46(b).При малых отклонениях частота w оказывается равной угловой частоте w₀ линейной системы второго порядка. По мере того, как амплитуда отклонений растет, период укорачивается или удлиняется в зависимости от того, стано­вится пружина более жесткой или менее жесткой (β > 0 или β < 0). Следует заметить, что теперь колебаниеl=l(t) уже не является чисто синусоидаль­ным, а помимо основной гармоники содержит гармоники высших порядков. Форма колебания также меняется с ростом амплитуды отклонений. Колеба­ние является синусоидальным только при очень малых отклонениях.

Из нашего рассмотрения следует, что в случае нелинейных систем нельзя говорить о частотной характеристике, так как поведение системы теперь зависит от амплитуды! Принцип суперпозиции более не действует, и, какмы увидим дальше, динамическое поведение таких систем может быть са­мым удивительным.

Предположим теперь, что затухание уже не равно нулю (D_t≠ 0) и на систему действует синусоидальная внешняя возбуждающая силаF_d = F_d (t) с постоянной амплитудойF_d. На рис. 2.47 показано, что случится с такойсистемой, если пружина постепенно становится более жесткой (β > 0). На этом графике приведена зависимость амплитуды l = l (t) основной гармо­ники от частоты возбуждения w.

Чтобы построить эту зависимость, необходимо отфильтровать частоту основной гармоники, совпадающую с частотой прилагаемого извне сило­вого воздействия, из (искаженного) сигнала l(t). Здесь мы приводим только амплитуду этой основной гармоники (линеаризированное поведение). Как видим, резонансная кривая больше не имеет того привычного вида, который

Рис 2 47. Зависимость амплитуды основной гармоники вынужденных колеба­ний нелинейной системы «пружина с грузом» от частоты синусоидального воздействия постоянной амплитуды при наличии демпфирования (в случае, когда жесткость пружины увеличивается).

характерен для линейной системы второго порядка и показан на рис. 2.45(а). Она теперь наклонена в сторону более высоких частот; другими сло­вами, она теперь перекошена. Если амплитуда F_d синусоидального воздей­ствия меняется, то пик резонансной кривой будет перемещаться по штри­ховой линии, которая является характеристикой свободных колебаний (какна рис. 2.46(b), β > 0).

Если частота возбуждающей силы увеличивается, но амплитуда F_d оста­ется постоянной, то выходная величина в системе «пружина с грузом» вне­запно падает до много меньшего уровня(явление перескока) после того, как на частотеw= bw₀достигается пик резонансной кривой. Когда частота умень­шается (опять же при неизменной амплитуде входного воздействия), амп­литуда основной гармоники в сигналеl(t)вдруг скачком переходит к боль­шему значению на частоте w = aw_0. Следовательно, в интервале частот bw₀ ≤ w ≤ bw₀ система неустойчива. Установившийся режим никогда не может принадлежать кривой, изображенной точками внутри этого интервала. Мы видим, что резонансные кривые такого рода нелинейных механических си­стем обладают гистерезисом.

Если мы теперь вдобавок станем изменять амплитуду возбуждающей силы f_d(t), то получим резонансные кривые, представленные на рис. 2.48. На рис.2.48(а) показаны характеристики системы «пружина с грузом» в случае, когда жесткость пружины постепенно увеличивается, а на рис. 2.48(b) — для случая, когда жесткость пружины уменьшается.

1. (b)

Рис. 2 48 Влияние амплитуды входного воздействия на резонансные кривые (см рис 2 47) нелинейной системы «пружина с грузом» при наличии демпфи­рования. На рис. (а) представлен случай, когда жесткость пружины увеличива­ется (b > 0), а на рис. (b) показаны амплитудно-частотные характеристики для случая, когда пружина постепенно становится мягче (b < 0).

Наконец, обратим внимание на тот факт, что у систем такого рода при возбуждении их синусоидальным воздействием, помимовысших гармоник на частотах kw, могут наблюдаться субгармоники на частотах w / п (здесь k и п — целые числа). Обычно это происходит при малом, но не равном нулю затуханииD_t.

Приведенный иллюстративный пример поведения нелинейной динами­ческой системы ясно показывает, насколько сложными могут быть эти сис­темы. Это обстоятельство является одной из причин, по которым в измери­тельных системах стараются избежать сколько-нибудь существенной (дина­мической) нелинейности: система становится слишком сложной.