3.5.3 Электронная регистрация

У рассмотренных методов регистрации скорость записи сильно ограничена, поскольку для реализации каждого из них требуются движущиеся механи­ческие части. Часто, однако, бывает желательно зарегистрировать процесс, протекающий с высокой скоростью, для последующего изучения и анализа. Это можно сделать с помощью быстрой твердотельной памяти. Если из вход­ного сигнала с очень высокой частотой берутся выборки и заносятся в полу­проводниковую память, то позднее их можно будет считать оттуда со значи­тельно меньшей скоростью и представить их для наблюдения с помощью осциллографа, например, или с использованием перьевого самописца. В ре­зультате мы получим реальное растяжение временной шкалы. Таким путем можно осуществить изменение временного масштаба в 10⁹ раз (так что на­носекунда становится секундой). Это эквивалентно тому, как если бы на­блюдаемое явление происходило в 10⁹ раз медленнее. Приборы, с помощью которых это можно сделать, называют устройствами для регистрации быст­ропротекающих процессов. Необходимо отметить, что хотя в стробоскопи­ческом осциллографе также берутся выборки входного сигнала (см. пара­граф 4.4), с его помощью можно осуществлять индикацию только периоди­ческих сигналов, поскольку принцип его действия основан на взятии коге­рентных выборок (см. параграф 2.2). В осциллографе такого типа сигналы не запоминаются, а непосредственно индицируются на экране.

Рис. 3.84 поясняет принцип действия устройства для регистрации пере­ходных (быстропротекающих) процессов. Этот прибор иногда называют оциф­ровывающим осциллографом, в котором осуществляется дискретизация, хотя это название включает в себя уже упомянутый стробоскопический осцил­лограф. Существенной функцией устройства для регистрации переходных процессов является то, что с его помощью можно регистрировать как пери­одические, так и апериодические (переходные) сигналы, которые можно выводить для наблюдения позднее со значительно меньшей скоростью и в периодическом режиме.

Электронное устройство для регистрации переходных процессов работа­ет следующим образом. Сначала из входного сигнала в расположенные на равном расстоянии друг от друга моменты времени берутся выборочные значения, которые с помощью аналого-цифрового преобразователя (АЦП) переводятся в форму цифровых данных. Эти данные записываются в цикли­ческую полупроводниковую память. В отсутствие сигнала запуска этот про­цесс происходит непрерывно и новые данные постоянно записываются по­верх старых данных. Памятью (длиной слова и числом сохраняемых слов) определяется разрешающая способность по амплитуде и длительность запи­си. По сигналу запуска сравнивающее устройство пeреводит счетчик в активный режим.

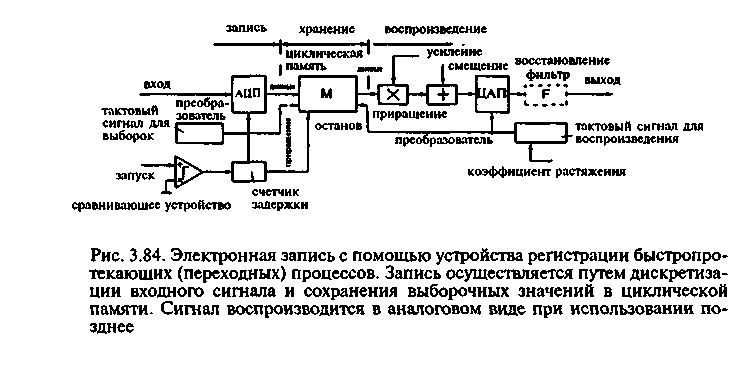
Этим счетчиком, в который извне заносится определенное начальное значение, определяется число выборок, которое будет занесено в полупроводниковую память до того, как процесс циклического запомина­ния будет остановлен. Если, например, объем памяти составляет 4000 слов, а в счетчик задержки в качестве начального значения заносится число 2000, то к моменту, когда содержимое счетчика станет равным нулю, в памяти окажутся заполненными 2000 выборок до момента действия сигнала запуска и 2000 выборок после этого момента. Поскольку частота тактового сигнала, с которой берутся выборки, точно известна заранее, восстанавливаемый сиг­нал содержит информацию не только о величине, но также и о форме сиг­нала как функции времени. Если, например, частота тактового сигнала ус­тановлена равной 500 МГц, то мы сможем зарегистрировать сигнал в преде­лах интервала длительностью ±4 мкс по обе стороны от момента запуска; выборки берутся каждые 2 не. Процедура непрерывной записи поверх старых данных, прерываемая в момент времени, задержанный на определенную величину по отношению к моменту запуска, позволяет нам наблюдать со­бытия, происходившие перед тем, как произошел пуск. После того, как ус­тройство для регистрации переходных процессов остановлено, сигнал в форме цифровых данных сразу же становится доступным для обработки на компь­ютере. Эти данные можно также вновь преобразовать в аналоговый сигнал, как указано на рис. 3.84. Восстанавливаемый сигнал можно воспроизводить в любом (регулируемом) темпе, который определяется частотой генератора тактового сигнала для воспроизведения. Продолжая начатый пример, пред­положим, что восстановление сигнала происходит со скоростью 5 выборок в секунду; тогда 10 нc входного сигнала будут соответствовать 1 секунде выходного сигнала (коэффициент растяжения равен 10⁸). В этом случае сиг­нал можно было бы изобразить на перьевом самописце, и это заняло бы в целом 13,3 минуты. Если генератор тактового сигнала, используемого при воспроизведении, поставлен в такой режим работы, что осуществляется сканирование только части памяти, можно реализовать «лупу времени» и наблюдать только самую интересную часть сигнала. При обратном преобра­зовании сигнала в аналоговое напряжение совсем легко изменить величину сигнала (усилить его или ослабить) путем умножения в цифровом виде; можно также ввести смещение (добавляя двоичное число).

Для того, чтобы при аналоговом восстановлении получалась верная копия входного сигна­ла, необходимо сгладить скачкообразные приращения выходного сигнала цифро-аналогового преобразователя (ЦАП), пропустив этот сигнал через фильтр нижних частот. Мы еще вернемся к так называемым восстанавлива­ющим фильтрам в параграфе 4.5. Для правильного восстановления частота (первичных) выборок должна по крайней мере вдвое превышать частоту наиболее высокочастотной составляющей входного сигнала. С этим мы так­же встретимся в параграфе 4.5. При скорости взятия выборок 500 МГц, как мы предположили в нашем примере, ширина спектра входного сигнала дол­жна быть меньше 250 МГц. Правда, на практике, чтобы сделать ошибки малыми (5%-ными), полосу частот, занимаемую входным сигналом, следу­ет ограничить 50 МГц.

Очевидно, что частотный диапазон устройства для регистрации переход­ных процессов определяется частотой, с которой берутся первичные выбор­ки (темп извлечения из памяти вторичных выборок определяется частотой тактового генератора, используемого при восстановлении сигнала). Время, необходимое для взятия каждой первичной выборки, зависит от быстродей­ствия схемы фиксации выборок, процедуры преобразования и записи в па­мять. Поэтому взамен непосредственному эквидистантному взятию выборок изобретен ряд других способов (рис. 3.85). На рис. 3.85(а) выборки из сигнала берутся быстро (в том темпе, в каком изменяется сам сигнал) при равных интервалах времени между выборками. Это как раз тот случай, который мы рассматривали до сих пор. Его называют взятием выборок «в реальном мас­штабе времени» и для него необходимы чрезвычайно быстрые схемы взятия выборок и АЦП.

На рис. 3.85(b) показано, что выборки из того же самого сигнала можно сделать поочередно, по принципу стробоскопа. Однако теперь сигнал обязан быть периодическим!. В первом периоде сигнала выборка берется в точке «1». В следующем периоде выборка берется в точке «2». (На самом деле, схема взятия выборок может пропускать целое число периодов перед тем, как взять следующую выборку.) Ясно, что при таком методе преобразование и запись в память могут выполняться тогда, когда это возможно; имеется масса вре­мени. Трудность заключается в той точности, с какой надо поддерживать временные соотношения между моментами взятия выборок и периодом вход­ного сигнала. Если в результате пропускания периодов время между выбор­ками растет, то становится все труднее соблюдать когерентность выборок по отношению к измеряемому сигналу. С другой стороны, чем меньше перио­дов входного сигнала заключено между соседними выборками, тем быстрее должны срабатывать соответствующие схемы.

На рис. 3.85(с) представлен гибридный способ взятия выборок, называ­емый дискретизацией со случайным повторением. В течение первого перио­да сигнала выборки берутся с крупным шагом в точках, помеченных циф­рой «1» на равном расстоянии друг от друга. Во втором периоде (снова возможно, после того как пропущено несколько периодов) выборки берут­ся с тем же самым шагом между моментами взятия выборок.,

Однако эти моменты, помеченные цифрой «2», расположены совершенно случайно по отношению к моментам взятия выборок в первом периоде. В данном случае больше нет необходимости в когерентности выборок с входным сигналом. Необходимо только, чтобы удовлетворялись два требования: расстояние между выборками должно оставаться постоянным, а сигнал должен быть периоди­ческим. Для того, чтобы можно было восстановить входной сигнал, нужно просто измерить расстояние между моментом запуска и моментом времени, задаваемым тактовым сигналом, используемым при взятии выборок.

4

Электронные измерительные системы

Некоторые комбинации устройства обработки сигнала и индикации в изме­рительных системах применяются так часто, что они стали самостоятельны­ми приборами. В частности, они используются в оборудовании, созданном для измерения таких основных величин, как частота, амплитуда тока или напряжения, сопротивления и т. д. Приборы, предназначенные для наблю­дения периодически повторяющихся сигналов, такие как осциллограф для анализа во временной области или анализаторы спектра для анализа в час­тотной области, также попадают в эту категорию. Фактически упомянутые величины измеряются исключительно с помощью электронных приборов. В этой главе мы рассмотрим некоторые из таких электронных измерительных систем.

4.1 Измерение частоты

Частота повторения явления определяется как число, показывающее, сколько раз это явление происходит за единицу времени. Интервал времени между двумя повторениями называется периодом Т. Следовательно, частота и пе­риод связаны соотношением f = 1 / Т. Поэтому измерение частоты часто можно заменить измерением временного интервала и наоборот.

Существует много методов измерения частоты электрического сигнала. Один из них — резонансный метод, который применялся раньше в частото­мерах, содержавших набор стержней, вибрирующих под воздействием вход­ного сигнала. Стержни имеют слегка различающиеся резонансные частоты. Частота входного сигнала принимается приблизительно равной резонанс­ной частоте стержня с наибольшей амплитудой вибраций. (Этот метод изме­рения применялся для определения линейной частоты вспомогательных си­ловых генераторов переменного напряжения.)

Другой метод измерения частоты основан на преобразовании частоты в напряжение (см. рис. 4.1). Здесь входной сигнал сначала преобразуют в сигнал

прямоугольной формы. Нарастающий фронт прямоугольного колебания за­пускает ждущий мультивибратор, который вырабатывает синхронизован­ный с входным сигналом узкий импульс с фиксированными амплитудой V и длительностью Т. Затем эти импульсы пропускаются через фильтр нижних частот и их среднее значение (постоянная составляющая) индицируется стрелочным прибором. Диапазон преобразователя частоты в напряжение та­кого типа составляет приблизительно две декады. На высоких частотах он ограничен временем нарастания прямоугольных колебаний, а также време­нем нарастания и спада импульсов ждущего мультивибратора. На низких частотах ограничение обусловлено фильтром нижних частот. Частота среза этого фильтра должна быть достаточно низкой, чтобы минимизировать пуль­сации выходного сигнала, поступающего на стрелочный прибор. Эти пуль­сации являются следствием неполной фильтрации импульсного напряже­ния V_B. Чтобы иметь возможность измерять низкие частоты, частота среза фильтра должна быть уменьшена, а это делает отклик системы очень инер­ционным.

Преобразователь временного интервала в напряжение не имеет последнего недостатка. Этот преобразователь создает напряжение, пропорциональное времени между двумя последовательными прохождениями входного сигна­ла через нуль. То есть здесь, в отличие от измерения частоты, фактически измеряется период. Первый шаг преобразования аналогичен указанному на рис. 4.1. Импульсами V_B синхронизируется генератор пилообразного напря­жения (см. рис. 4.2). Напряжение Vs создаваемое этим генератором, имеет строго определенный наклон и сбрасывается положительным фронтом им­пульсов V_B. В момент появления импульса, напряжение V_s достигает значе­ния, которое запоминается схемой хранения точно на один период. Полу­ченное таким образом выходное напряжение V₀ пропорционально измерен­ной длительности предыдущего периода. Для больших периодов диапазон измерения ограничен максимально достижимой амплитудой пилообразного напряжения. Для малых периодов ограничение обусловлено временем об­ратного хода пилообразного напряжения. Диапазон измерения также состав­ляет приблизительно две декады.

Чаще всего для измерения частоты и периода используется метод счета, применяемый в частотомерах и измерителях периода. Строго говоря, это название неправильно, поскольку считать можно только числа, а не вели­чины, имеющие физическую размерность, такие как частота или времен­ной интервал. В частотомере подсчитывается число колебаний измеряемого сигнала, попадающих в один период опорного сигнала точно заданной час­тоты. В измерителе периода процедура обратна описанной, то есть подсчи­тывается число периодов опорного сигнала, попадающих в один период измеряемого сигнала. Следовательно, с помощью одного и того же счетчика можно выполнять оба измерения, меняя местами два сигнала. Большая по­пулярность этого метода измерения, в основном, связана со стремительным развитием быстрых цифровых схем и наличием сверхстабильных и точных кварцевых управляемых генераторов.

Частотомер с помощью сравнивающего устройства преобразует входнойсигнал в сигнал прямоугольной формы той же самой частоты (см. рис. 4.3(а)). Пока вентиль открыт (пропускает сигнал), десятичный счетчик считает пе­риоды входного сигнала V_i .После того, как вентиль закроется, результат счета индицируется алфавитно-цифровым дисплеем. Длина временного ин­тервала, в течение которого вентиль открыт (время счета), определяется частотой f₀ опорного генератора. Эта частота f₀ делится перестраиваемым делителем частоты с коэффициентом деления кратным 10 (декадным счет­чиком). Время счета при этом устанавливается равным половине одного пе­риода колебания, полученного делением частоты опорного колебания. Сле­довательно, частоту сигнала, управляющего вентилем, следует еще раз по­делить на 2 на пути от выхода декадного счетчика до вентиля, учитывая, что вентиль открыт при низком управляющем напряжении и закрыт при высо­ком. Тогда время счета равно 10ⁿ / f₀, где п — установленное число разрядов декадного счетчика (который делит на 10"). Таким образом, число подсчи­танных периодов входного сигнала в конце времени счета равно:

где f _i частота входного сигнала. Видно, что метод счета используется,

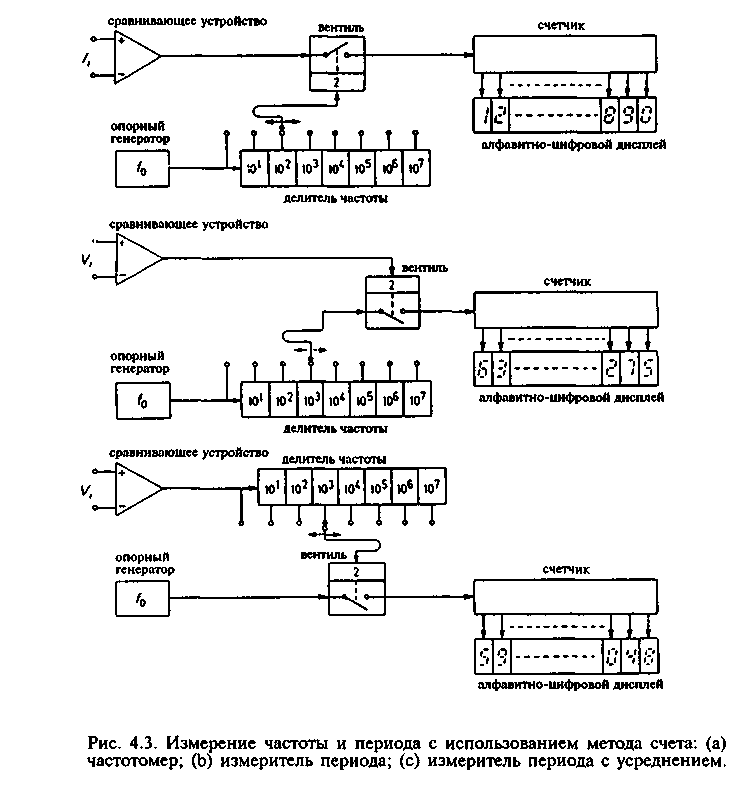
чтобы найти отношение; мы определяем величину f_i по отношению кf_i По­этому опорная частота f₀ должна быть задана точно.

Опорный сигнал генерируется кварцевым генератором. Хороший срез кристалла кварца можно использовать как механический резонатор с очень высокой добротностью (10⁶—10⁷). Пьезоэлектрический кристалл применяет­ся для стабилизации частоты генерируемых колебаний. Часто всю схему ге­нератора помещают в термостат с целью поддержания постоянной темпера­туры, даже в то время, когда генератор не используется. Таким образом достигается кратковременная стабильность 5x10^-11 в час и уход частоты — из-за старения — менее чем 5x10^-10 в день.

Максимальная частота, которую можно измерить таким способом, опре­деляется быстродействием цифровых счетчиков. Этим способом можно еще измерять частоту до 150 — 200 МГц. Нижний предел частоты определяется длительностью времени счета, необходимого для подсчета достаточного числа периодов

Накопление достаточно большого числа периодов необходимо для получения малой ошибки квантования, которая всегда имеет место при сче­те в пределах строба. Поскольку момент переключения вентиля не связан с моментом пересечения нуля входным сигналом, ошибка квантования равна плюс или минус одному периоду входного сигнала.

Особенно это проявляется на низких частотах, когда счетчик и дисплей заполнены не полностью и ошибка квантования приводит к относительно большой погрешности измерения частоты.

Пусть, например, частота f₀ равна 1 МГц, а максимальный коэффици­ент деления частоты п = 10⁷. Тогда наибольшее время счета, которое можно выбрать, составляет 10 с. Частота, точно равная 900 кГц, будет индициро­ваться как 9000000  1, в то время как результатом измерения частоты 9 Гц будет 901. Следовательно, ошибка квантования в частотомере обратно пропорциональна измеряемой частоте. Очевидно, что она изменяется также обратно пропорционально времени счета.

На низких частотах предпочтительнее заменить измерение частоты на измерение периода. Это легко достигается перестановкой входного сигнала и сигнала опорного генератора (см. рис. 4.3(b)). Время счета теперь равно периоду1 /f_i входного сигнала V_i и в течение этого интервала теперь подсчиты­ваются периоды опорного колебания. Таким образом, результат счета в кон­це времени счета равен:

Вотличие от предыдущего случая число, накопленное в счетчике, будет тем больше, чем ниже частота f _i .Следовательно, по мере понижения часто­ты влияние ошибки квантования (член ±1 в выражении для с) становится меньше. Относительная ошибка квантования при измерении периода про­порциональна частоте входного сигнала. (Противоположный результат на­блюдается в случае измерения частоты: ошибка уменьшается с повышением частоты.) При измерении периода относительная ошибка квантования об­ратно пропорциональна поделенной частоте 10ⁿ / f₀ опорного колебания.

При измерении периода в дополнение к ошибке квантования возникает еще одна ошибка из-за погрешности в задании времени счета. Как можно видеть из рис. 4.4, входной сигнал У содержит шум, искажения и помехи. Поэтому момент прохождения входного сигнала через нуль не будет точно совпадать с моментом пересечения нуля чистым сигналом. В примере, пока­занном на рис. 4.4, время счета больше не равно Т, а составляет величину Т + T₁ + T₂ . Относительная ошибка времени счета определяется соотноше­нием (T₁+T₂)/T. По мере увеличения наклона dV_i/dt при прохождении входного сигнала V_i через нуль, ошибка времени счета будет уменьшаться, если искажения сохраняются прежними. Очевидно, что идеальным является входной сигнал прямоугольной формы.

Вклад ошибок времени измерения и ошибок квантования в результиру­ющую ошибку можно уменьшить используя метод усреднения периода, (см. рис. 4.3(с)). Здесь частота f_i входного сигнала делится декадным счетчиком на 10ⁿ. Это фактически соответствует умножению числа подсчитанных перио­дов входного сигнала на 10ⁿ Теперь та же самая ошибка времени счета при­ходится на много большее время счета. Относительная погрешность времени счета обратно пропорциональна числу периодов, по которым проведено усреднение. Это применимо также к ошибке квантования, поскольку число, накопленное в счетчике дисплея, увеличивается с числом усредняемых пе­риодов.

На рис. 4.5 изображено порознь влияние ошибки квантования, ошибок времени измерения и ошибок опорной частоты f₀ при различных значениях измеряемой частоты f_i входного сигнала. Вклад погрешности частоты опор­ного колебания f₀ в относительную ошибку измерения £ не зависит от из­меряемой частоты f_i Реалистическая оценка ошибки такого типа дает вели­чину ЗхЮ-⁷. Вклад ошибки квантования зависит от частоты. При измерении частоты ошибка квантования обратно пропорциональна значению измеряе­мой частоты f_i. При измерении периода она пропорциональна частоте f_i .Это определяет наклоны прямых на рис. 4.5. Погрешность квантования обратно пропорциональна времени счета, а также обратно пропорциональна числу периодов, по которым проводится усреднение. Таким образом, возникает семейство прямых. Абсолютное положение каждой из этих линий можно определить следующим образом. Если измеряемая частота f_i равна 1 МГц, а время счета точно равно 1 с, то на индикаторе получим значение 1000000. Относительная ошибка квантования при этом равна £ = 10^-6. Этот случай отмечен на рис. 4.5 точкой A. Если измерение периода выполняется только по одному периоду и при частоте входного сигнала 10 кГц индицируется число 100, то относительная ошибка квантования составляет 10^-2 .

На рис. 4.5 это соответствует точке В. На низких частотах погрешность измерения периода определяется ошибкой времени счета. Предположение о том, что отноше­ние сигнал/шум на входе не зависит от частоты, приводит к постоянной относительной ошибке времени счета. Реальная величина этой ошибки рав­на Зх10^-4. Если выполнено усреднение по 10ⁿ периодам, то ошибка времени счета уменьшится в 10ⁿ раз. Ошибка времени измерения приводит к вырав­ниванию графиков ошибки в левой части рис. 4.5.