
ПСИИ / skobcov_yu_a_osnovy_evolyucionnyh_vychislenii
.pdf211
меньше значение фитнесс-функции. Данная фитнесс-функция является также стандартизованной, так как случае для идеального решения дает нулевое значение.
Часто в качестве фитнесс-функции также используют квадратичную
ошибку f s = ∑n (yi −di )2 . Таблица 7.8 показывает различие для этих двух
i=1
фитнесс-функций в том случае, если на некотором (промежуточном) этапе в качестве особи оценивается (плохо обученная) программа, реализующая функцию f (x) = x 2 .
|
|
|
|
|
Таблица 7.8. |
|
|
|
|
|
|
|
|
№ |
Вход x |
Выход d |
Выход y |
Ошибка f a |
Ошибка fs |
|
|
|
|
|
|
|
|
1 |
1 |
2 |
1 |
1 |
2 |
|
|
|
|
|
|
|
|
2 |
2 |
6 |
4 |
2 |
4 |
|
|
|
|
|
|
|
|
3 |
4 |
20 |
16 |
4 |
16 |
|
|
|
|
|
|
|
|
4 |
7 |
56 |
49 |
7 |
49 |
|
|
|
|
|
|
|
|
5 |
9 |
90 |
81 |
9 |
81 |
|
|
|
|
|
|
|
|
|
|
Общая ошибка |
|
23 |
151 |
|
|
|
|
|
|
|
|
Мы рассмотрели использование в качестве фитнесс-функции ошибки в двух метриках, которые характерны для применения ГП в качестве символьной регрессии, что будет детальнее рассмотрено в разделе 7.8. Подобный подход применяется также во многих других задачах, где используются следующие фитнесс-функции:
1)число правильно отображаемых пикселов в задачах обработки изображений;
2)число столкновений робота со стенами при обучении обхода препятствия;
3)число правильно классифицируемых примеров в задачах классификации;
212
4)ошибка между реальными и ожидаемыми значениями в задачах прогнозирования;
5)приз победителя в игровых задачах;
6)количество «пищи», найденной агентом, в многоагентных системах («искусственная жизнь» и т.п.)
Естественно разработано множество фитнесс-функций других типов, их вид существенно зависит от исследуемой проблемы, а применение ГП не ограничивается задачами символьной регрессии. Кроме приведенных стандартных разработано много других методов определения фитнесс-функции, в частности теоретико-игровых и основанных на идее коэволюции, где особи соревнуются между собой без явного вычисления значений. В некоторых случаях, кроме близости решений учитываются и другие критерии, например, длина или время выполнения программы. В этом случае говорят о многокритериальных фитнесс-функциях.
7.7. Интроны
Программы, построенные с помощью методов ГП, имеют тенденцию к накоплению интронов – ненужных и непригодных участков кода.
Например:
(NOT (NOT x)),
(AND (ORXX)), (+… (-XX)), (+X0),
(*X1), (*(DIV XX)),
(MOVE_LEFT MOVE_RIGHT), (IF (2=1) . . . ),
A:=A.
213
Таких фрагментов в программе возникает достаточно много (их количество может достигать 60%), и обнаружение и удаление интронов представляет серьезную проблему в ГП. Разработаны специальные методы для их устранения. Интересно отметить, что в живой природе интронов также достаточно много (в частности, на генном уровне существуют "лишние" участки ДНК).
7.8. Общий алгоритм генетического программирования
Таким образом, для решения задачи с помощью ГП необходимо выполнить описанные выше предварительные этапы:
1)Определить терминальное множество;
2)Определить функциональное множество;
3)Определить фитнесс-функцию;
4)Определить значения параметров, такие как мощность популяции, максимальный размер особи, вероятности кроссинговера и мутации, способ отбора родителей, критерий окончания эволюции (например,
максимальное число поколений) и т.п.
После этого можно разрабатывать непосредственно сам эволюционный алгоритм, реализующий ГП для конкретной задачи. Как и в случае ГА здесь также возможны различные подходы, которые рассмотрены в разделах 4-5.
Например, решение задачи на основе ГП можно представить следующей последовательностью действий.
1)установка параметров эволюции;
2)инициализация начальной популяции;
3)t:=0;
4)оценка особей, входящих в популяцию;
5)t:=t+1;
214
6)отбор родителей;
7)создание потомков выбранных пар родителей – выполнение оператора кроссинговера;
8)мутация новых особей;
9)расширение популяции новыми порожденными особями;
10)сокращение расширенной популяции до исходного размера;
11)если критерий останова алгоритма выполнен, то выбор лучшей особи в конечной популяции – результат работы алгоритма. Иначе переход на шаг 4.
Следует отметить, что в ГП достаточно часто применяется асинхронный ГА, рассмотренный в 4.6.
7.9. Символьная регрессия
Этот раздел является одним из важнейших приложений ГП. Данный термин подчеркивает то, что здесь объектом поиска является символьное описание модели, в отличие от множества коэффициентов в стандартних методах. Этот поход существенно отличается от других методов регрессии и использования нейросетей прямого распространения, где структура (и сложность) модели предполагается известной и фактически необходимо найти только ее коэффициенты. В случае символьной регресии вид и сложность функции заранее неизвестны и могут изменяться в процессе поиска.
Задача регрессии может быть определена на основе множества значений входных независимых переменных x и зависимой выходной
переменной |
y. Целью поиска является апроксимация |
y с помощью |
переменных |
x и коэффициентов w следующим образом y = f (x, w) +ε , где ε |
|
представляет шум (ошибку). |
|
|
215
В стандартних методах регресии вид функции f предполагается известным, например, в линейной регресии f (x, w) = w0 + w1x1 +... + wn xn . Здесь коэффициенты wi обычно находятся методом наименьших квадратов. В нелинейных методах, например, с использованием нейронных сетей прямого распространения функция имеет вид f (x, w) = w0 • g(wh x) . Здесь коэффициенты w0 и wh представляют синаптические веса нейронной сети выходного и скрытых слоев соответственно.
Как уже отмечалось, символьная регрессия на основе ГП не использует некоторую заранее предопределенную форму функции Здесь функция f (x, w) представляется древовидной структурой и строится эволюционным методом с использованием определенного функционального и терминального множеств. В качестве фитнесс-функции обычно используется квадратичная ошибка, которая оценивает качество решения и обеспечивает обратную связь при поиске решения. Для определенности обозначим функции множества, зависящие от одной переменной через h1,…, hk и функции от двух переменных как g1,…, gl. В этой нотации функция f (x, w) представляется в виде суперпозиции функций hi , gj, и например, может иметь следующий вид
Заметим, что в символьной регрессии при поиске решения не используются численные методы, например, градиентные или стохастические.
Далее рассмотрим детально пример использования символьной регрессии из [27] для апроксимации данных, представленных в табл.7.9. Необходимо найти функцию f(x), которая апроксимирует с заданной точностью эти «экспериментальные» данные.
Для решения задачи определим в соответствии с вышесказанным:
1.Терминальное множество: переменная x и константы в диапазоне [- 5,5];
216
2.Функциональное множество: арифметические функции +, - , * , % (защищенное деление).
3.Фитнесс-функция – стандартизованная на основе корня квадратного средней квадратичной ошибки.
4.Параметры: мощность популяции, методы инициализации популяции и отбора родителей, значения вероятностей кроссинговера и мутации.
|
|
Таблица 7.9 |
|
|
|
№ |
Вход x |
Выход y |
|
|
|
1 |
0.000 |
0.000 |
|
|
|
2 |
0.100 |
0.005 |
|
|
|
3 |
0.200 |
0.020 |
|
|
|
4 |
0.300 |
0.045 |
|
|
|
5 |
0.400 |
0.080 |
|
|
|
6 |
0.500 |
0.125 |
|
|
|
7 |
0.600 |
0.180 |
|
|
|
8 |
0.700 |
0.245 |
|
|
|
9 |
0.800 |
0.320 |
|
|
|
10 |
0.900 |
0.405 |
|
|
|
Koza [5] ввел следующую удобную и «прозрачную» форму для перечисления параметров , которая представлена в табл.7.10.
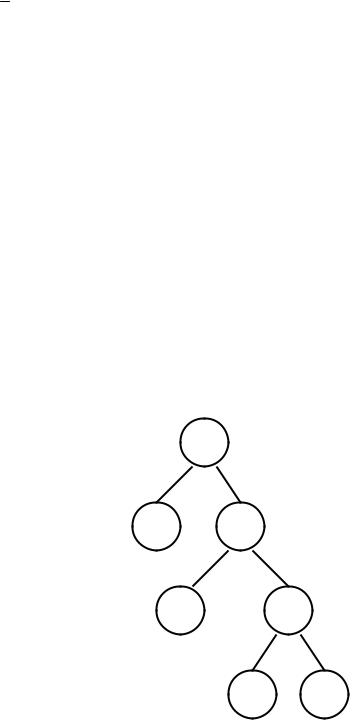
217
Далее приведем некоторые полученные экспериментальные данные результатов эволюции для различных запусков программ из [27]. В начальной популяции после инициализации лучшая особь представлена деревом рис.7.15, которая реализует (не минимальным образом !) функцию
f0 (x) = 3x .
Впоследующих рисунках рис.7.16 –7.20 представлены лучшие особи
последующих поколений. Здесь в первом поколении лучшая особь
реализует |
f1 (x) = |
|
x |
|
и соответствующее дерево |
рис.7.16 сильно |
|||||||||
6 |
−3x |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||
избыточно. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||
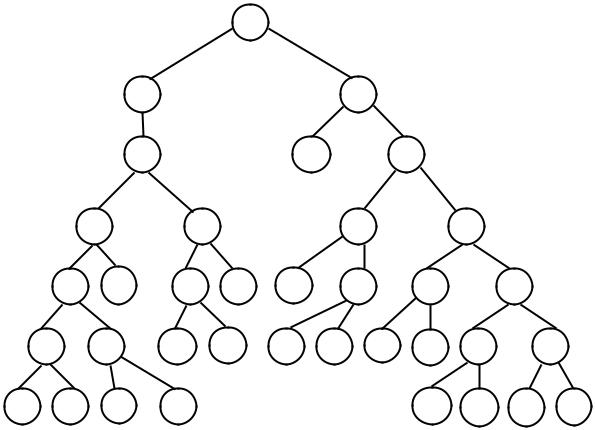
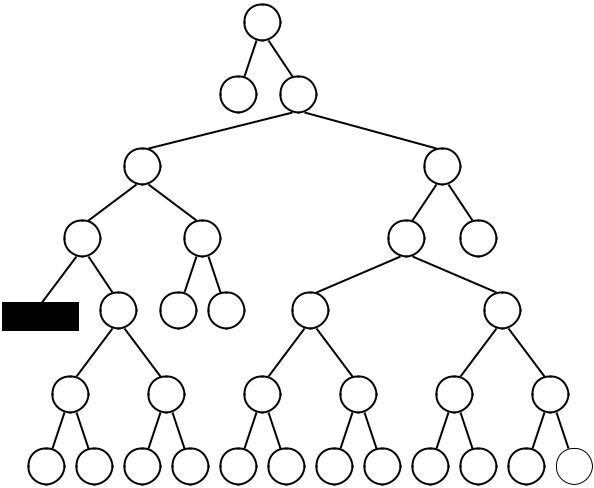
Аналогично во втором поколении лучшая особь реализует функцию |
|||||||||||||||
f 2 (x) = |
|
|
x |
|
|
|
|
|
|
|
|
и дерево тоже сильно избыточно. Наконец в |
|||
|
|
|
|
|
|
|
9(x +1) |
|
|
||||||
|
|
|
4 |
|
|
|
|
+ x |
|
|
|||||
|
x(x −4) |
−1+ |
|
− |
|
|
5x |
|
|||||||
x |
|
|
6 −3x |
|
|||||||||||
|
|
|
|
|
|
|
|
||||||||
третьем поколении получена лучшая особь f3 |
(x) = |
x 2 |
, которая дает |
|
|||
|
2 |
|
|
оптимальное решение в простейшей форме. |
|
|
|
% |
|
|
|
Х-
4,0 |
% |
ХХ
Рис.7.15. Лучшая особь в поколении 0.
|
218 |
|
Таблица 7.10 |
|
|
Параметры |
Значения |
|
|
Цель: |
Эволюция функции, |
|
апроксимируюшей данные |
|
Табл.7.6 |
|
|
Терминальное множество |
Переменная x, |
|
Целые от –5 до +5 |
|
|
Функциональное |
ADD, SUB, MUL, DIV |
множество |
|
|
|
Мощность популяции: |
600 |
Вероятность кросинговера: |
0.90 |
Вероятность мутации: |
0.05 |
Отбор родителей: |
турнирный с мощностью тура 4 |
Максимальное число |
100 |
поколений: |
|
Максимальная глубина |
|
после кроссинговера: |
200 |
Максимальная глубина |
4 |
мутации: |
|
Метод инициализации: |
Растущая |
|
|
|
|
219
%
|
|
|
- |
|
|
* |
|
|
|
|
|
|
|
% |
|
|
-1.0 |
|
* |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
% |
|
* |
|
% |
|
|
- |
|
|
- |
5.0 |
- |
x |
4.0 |
- |
|
* |
|
* |
|
|
|
|
|
||||||
|
+ |
% |
-1.0 |
-1.0 |
x |
x |
-3.0 |
x |
+ |
* |
|
|
|
|
|||||||
x |
1.0 |
0.0 |
x |
|
|
|
|
4.0 |
-1.0 |
1.0 -2.0 |
Рис.7.16. Лучшая особь поколения 1.
220
%
Х-
+ |
_ |
_ |
+ |
* |
2.0 |
Sub 1 |
+ |
1.0 |
y |
+ |
% |
|
|
|
|
% |
+ |
_ |
* |
+ |
_ |
-4.0 |
X |
-4.0 |
3.0 |
0 |
0 |
X |
X |
-4.0 |
X |
1.0 |
X |
Рис.7.17. Лучшая особь поколения 2.
