ТОТ (лекции) / ТД(лекц_я 4)

9

Л е к ц і я 1.4. Аналіз термодинамічних процесів з ідеальним газом.

Задачі аналізу термодинамічних процесів ідеального газу і загальні аналітичні залежності. Ізохорний процес. Ізобарний процес. Ізотермічний процес. Адіабатний процес. Політропний процес та його узагальнююче значення. Якісний аналіз процесів за допомогою p-v і T-s діаграм.

Джерела інформації: [1], с.80-96; [2], с.44-56; [8], с.98-118;

Задачі аналізу та порядок його виконання. Задачею аналізу будь-якого термодинамічного процесу є установлення закономірностей зміни параметрів стану робочого тіла та виявлення особливостей перетворення енергії. Порядок виконання аналізу наступний: виводиться рівняння процесу у і координатах; установлюється залежність між основними параметрами робочого тіла на початку і в кінці процесу; визначаються зміни питомої внутрішньої енергії, питомої ентальпії та питомої ентропії процесу (процеси вважаються оборотними); розраховуються питомі робота і теплота процесу. До основних процесів, які мають велике значення як у практичному, так і теоретичному відношеннях, належать: ізохорний – при постійному об'ємі; ізобарний – при постійному тиску; ізотермічний – при постійній температурі; адіабатний – без зовнішнього теплообміну.

Ізохорний процес. Процес при постійному об'ємі зветься ізохорним (v=const і dv=0). У p – v координатах графік процесу (ізохора) – пряма лінія, яка паралельна осі ординат (рис. 4.1, а). З рівняння стану ідеального газу маємо рівняння ізохорного процесу:

. (4.1)

Таким чином при v=const тиск газу змінюється прямо пропорційно його абсолютній температурі: , а термодинамічна робота газу дорівнює нулю .

Питома корисна (наявна) робота, яка може бути передана зовнішньому об'єкту, дорівнює:

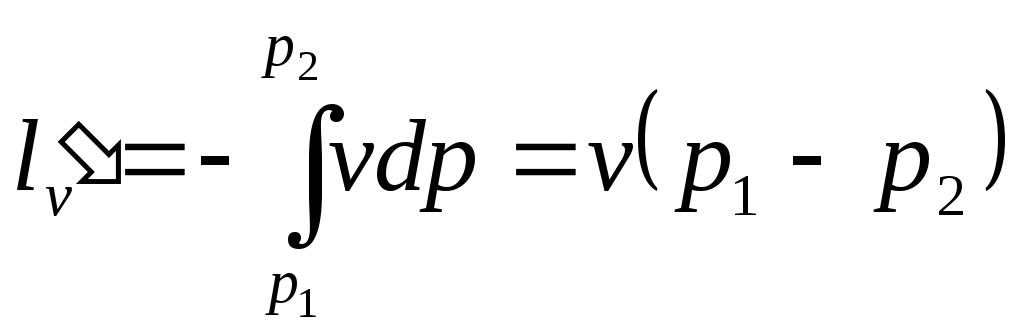. (4.2)

Рівняння першого закону термодинаміки для ізохорного процесу прийме вид , а питома теплота процесу при постійній теплоємності дорівнює:

. (4.3)

Вся зовнішня теплота у ізохорному процесі витрачається тільки на зміну внутрішньої енергії тіла. При змінній теплоємності у процесі

, (4.4)

де – середня питома ізохорна теплоємність у інтервалі температур .

Якщо процес здійснюється зі збільшенням тиску, теплота підводиться, при цьому збільшуються внутрішня енергія і температура газу. Навпаки, якщо тиск у процесі знижується, теплота відводиться , а внутрішня енергія і температура газу зменшуються.

Зміна питомої ентальпії ():

, (4.5)

де – середня питома ізобарна теплоємність у інтервалі температур .

Зміну питомої ентропії у оборотному процесі можна знайти з рівняння

. (4.6)

Для ізохорного процесу і , тому

. (4.7)

З цього рівняння виходить, що залежність ентропії від температури у ізохорному процесі має логарифмічний характер (рис. 4.2, б). Піддотична до ізохори 1-2 на рис. 4.2 у будь-якій точці дає значення істинної теплоємності . Ізохори різних об'ємів є еквідистантними кривими (процеси 1-2 і 1_а-2_а), які мають при однакових температурах однакові кутові коефіцієнти і обернені випуклістю донизу. Чим більше об'єм газу, тим далі знаходиться ізохора від осі ординат.

а б

Рис. 4.1. Графіки ізохорного процесу у p-v координатах (а) і T-s координатах (б)

Схема енергетичного балансу для ізохорного процесу показана на рис. 4.2. Частка питомої теплоти, яка витрачається на зміну внутрішньої енергії ідеального газу у ізохорному процесі

. Рис.4.3

Рис. 4.2

Ізобарний процес. Процес при постійному тиску зветься ізобарним (p=const і dp=0). У p-v координатах графік процесу (ізобара) – горизонтальна пряма (рис. 4.3, а). З рівняння стану ідеального газу маємо рівняння ізобарного процесу:

. (4.8)

Таким чином при p = const об'єм газу змінюється прямо пропорційно його абсолютній температурі: , а наявна робота газу () дорівнює нулю. При розширенні газу його температура зростає, а при стисненні – зменшується.

Питома термодинамічна робота процесу

. (4.9)

Рівняння першого закону термодинаміки для ізобарного процесу прийме вид , а питома теплота процесу при постійній теплоємності дорівнює:

. (4.10)

Вся зовнішня теплота у ізобарному процесі витрачається на зміну ентальпії тіла. При змінній теплоємності у процесі

, (4.11)

де – середня питома ізобарна теплоємність у інтервалі температур .

Зміна питомої внутрішньої енергії ():

,

де – середня питома ізохорна теплоємність у інтервалі температур .

Для оборотного процесу зміна питомої ентропії

, (4.12)

але при , тому

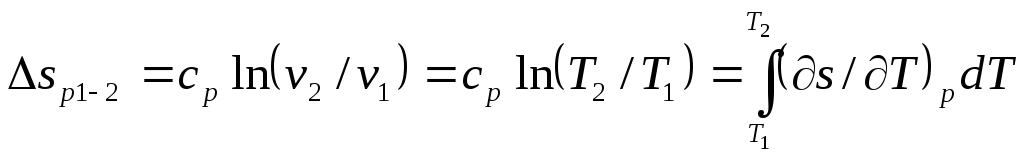. (4.13)

Ізобара на T – s діаграмі зображається логарифмічною кривою, яка обернена випуклістю донизу (рис. 4.3, б). Піддотична до кривої 1-2 у будь-якій її точці дає значення істинної теплоємності с_р. Усі ізобари є еквідистантними кривими, які мають при однакових температурах однакові кутові коефіцієнти. Чим більше тиск, тим ближче ізобара до осі ординат . Ізобара йде більш полого, ніж ізохора .

а б

Рис. 4.3. Графіки ізобарного процесу у p-v координатах (а) і T-s координатах (б)

Схема енергетичного балансу для ізобарного процесу показана на рис. 4.4. Частина теплоти , переходить у роботу розширення, а інша частина йде на збільшення внутрішньої енергії.

Частка теплоти, яка витрачається на зміну внутрішньої енергії ідеального газу у ізобарному процесі:

Рис. 4.4

Ізотермічний процес. Процес, який протікає при постійній температурі (T = const і dT = 0), називається ізотермічним, а графік процесу – ізотермою. Рівняння процесу витікає з рівняння стану ідеального газу

(4.14)

або

і . (4.15)

При постійній температурі об'єм газу змінюється обернено пропорційно його тиску. Термодинамічна робота процесу (робота зміни об'єму):

. (4.16)

У зв'язку з тим, що температура ізотермічного процесу T = const, внутрішня енергія і ентальпія ідеального газу також не змінюються (, ). Отже, відповідно до першого закону термодинаміки уся підведена до газу теплота повністю перетворюється у роботу розширення і розраховується за формулою (4.16) або

. (4.17)

Таким чином у ізотермічному процесі ідеального газу робота зміни об'єму, наявна робота і теплота, отримана тілом, рівні між собою: . При ізотермічному стисненні від газу відводиться теплота у кількості, яка дорівнює витраченій на стиснення роботі. Теплоємність ізотермічного процесу . Зміна ентропії у ізотермічному процесі:

. (4.18)

Графіком ізотермічного процесу у p – v координатах є рівнобічна гіпербола (рис. 4.5, а), а у T – s координатах – пряма, яка паралельна вісі абсцис (рис. 4.5, б).

а б

Рис. 4.5. Графіки ізотермічного процесу у p-v координатах (а) і T-s координатах (б)

Частка теплоти, яка витрачається на зміну внутрішньої енергії ідеального газу у ізотермічному процесі,

.

Схема енергетичного балансу для ізотермічного процесу показана на рис. 4.6.

Рис. 4.6

Адіабатний процес. Процес, при якому робоче тіла не обмінюється теплотою з навколишнім середовищем (), називається адіабатним, а графік процесу – адіабатою. Щоб здійснити такий процес, необхідно або теплоізолювати газ, тобто розмістити його у адіабатній оболонці, або здійснити процес настільки швидко, щоб зміна температури газу, зумовлена його теплообміном з навколишнім середовищем, була знехтувано малою у порівнянні зі зміною температури, викликаною розширенням або стисненням газу. Як правило, це можливо, бо теплообмін відбувається значно повільніше, чим стиснення або розширення газу. Оборотний адіабатний процес можна здійснити у циліндрі з абсолютно нетеплопровідними стінками при нескінченно повільному переміщенні поршня.

Для отримання рівняння адіабати, запишемо перший закон термодинамікм у двох формах з урахуванням того, що , , а :

,

.

Якщо поділити перше рівняння на друге і підставити , отримаємо

. (4.19)

Інтегруючи останнє рівняння при умові, що показник адіабати ,

знаходимо

.

Після потенціювання отримаємо рівняння адіабати

, (4.20)

або

. (4.21)

При адіабатному процесі добуток тиску на об'єм газу у степені k є величина постійна. З рівняння адіабати витікає, що

і . (4.22)

Якщо ці співвідношення підставити у рівняння для крайніх точок процесу, після перетворень знайдемо:

. (4.23)

Термодинамічна робота при адіабатному процесі згідно з першим законом термодинаміки здійснюється за рахунок зменшення внутрішньої енергії ідеального газу і може бути обчислена при за формулою:

,

а з урахуванням того, що ( і ),

або

. (4.24)

З урахуванням з останнього рівняння (4.24) отримаємо:

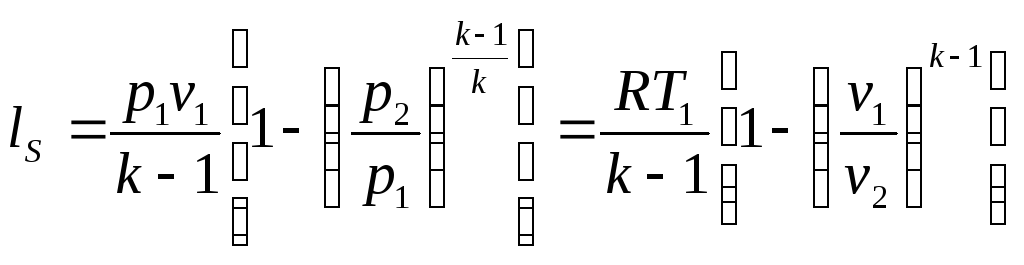
. (4.25)

При адіабатному процесі наявна робота у k разів більше термодинамічної роботи , що виходить з рівняння (4.19), отже

. (4.26)

Для оборотного адіабатного процесу , тому і , отже адіабатний процес є одночасно ізоентропійним . Теплоємність адіабатного процесу дорівнює нулю: = 0. У координатах адіабата зображається нерівнобічною гіперболою (рис. 4.7, а), яка йде крутіше за ізотерму, оскільки : при адіабатному розширенні тиск знижується швидше, ніж при ізотермному, тому що у процесі розширення зменшується температура газу. У координатах адіабата зображується вертикальною прямою (рис. 4.7, б). Необоротний адіабатний процес не є ізоентропійним і незалежно від його спрямованості як при розширенні , так і при стисненні супроводжується зростанням ентропії.

а б

Рис. 4.7. Графіки адіабатного процесу у p-v координатах (а) і T-s координатах (б)

Схема енергетичного балансу адіабатного процесу показана на рис. 4.8.

Доля теплоти, яка витрачається на зміну внутрішньої енергії ідеального газу у цьому процесі, не має смислу.

Рис. 4.8

Політропний процес і його узагальнююче значення. Кожний процес зміни стану робочого тіла, який відбувається при постійній теплоємності, зветься політропним, а графік процесу – політропою. Рівняння цього процесу можна отримати на основі першого закону термодинаміки, який, з урахуванням того що , і , можна записати

,

.

Поділивши друге рівняння на перше, отримаємо

.

Позначивши ліву частину останнього рівняння , отримаємо

. (4.27)

Після інтегрування рівняння (4.27) отримаємо рівняння політронного процесу:

_(4.28)

або

. (4.29)

Величина , яка залежить від теплоємност політропного процесу, зветься показником політропи. Показник політропи сталий для конкретного процесу. Значення його змінюється від до в залежності від теплоємності і визначає характер процесу. Політропний процес є узагальнюючим. Усі розглянуті вище процеси – його окремі випадки. Рівняння чотирьох основних термодинамічних процесів витікають з рівняння політропного процесу при таких значеннях показника політропи:

– ізобарний процес;

– ізохорний прпоцес;

– ізотермічний процес;

– адіабатний процес.

Оскільки рівняння політропи відрізняється від рівняння адіабати тільки значенням показника , усі співвідношення між основними параметрами для політропного процесу можуть бути представлені формулами адіабатного процесу, якщо показник адіабати замінити на показник політропи :

; ; . (4.30)

Рівняння термодинамічної роботи політропного процесу має аналогічний вид з рівнянням термодинамічної роботи адіабатного процесу

. (4.31)

Наявна робота політропного процесу по аналогії з адіабатним процесом дорівнює

. (4.32)

Теплоємність політропного процесу отримаємо з формули :

. (4.33)

Зміна питомої внутрішньої енергії і ентальпії газу у політропному процесі визначаються за формулами (4.4) і (4.5).

Кількість теплоти політропного процесу, виходячи з першого закону термодинаміки, дорівнює

, (4.34)

або

. (4.35)

Теплоємності основних процесів отримаємо з рівняння (4.33) при різних значеннях:

ізохорний процес ;

ізобарний процес ;

ізотермічний процес ;

адіабатний процес .

Значення у будь-якому політропному процесі можна знайти з рівняння (4.28), якщо маємо координати двох точок процесу:

отже . (4.36)

Зміна ентропії газу у політропному процесі

або для скінченного процесу

(4.37)

Характеристикою політропного процесу може бути частка питомої теплоти, яка витрачається на зміну внутрішньої енергії ідеального газу і визначається виразом

.

Якісний аналіз процесів за допомогою p-v і T-s діаграм. Політропний процес у і координатах зображується деякою кривою, положення якої залежить від показника політропи . Для того, щоб простежити за графіками політропних процесів при різних значеннях у і координатах, у тих самих координатах зображують графіки основних процесів: ізохорного, ізобарного, ізотермічного і адіабатного, за допомогою яких можна визначити положення політроп, а також знаки , , , і у цих процесах. Наприклад, графік політропного процесу з проходить між графіками ізотермічного і адіабатного процесів. Усі процеси починаються в одній точці (рис. 4.9).

Рис. 4.9. Графіки політропних процесів у p-v координатах (а) і T-s координатах (б)

Ізохора поділяє поле діаграми на дві області: процеси, які знаходяться правіше ізохори, характеризуються додатною роботою, бо супроводжуються розширенням робочого тіла; для процесів, які знаходяться лівіше ізохори, робота від’ємна.

Процеси, які розташовані правіше і вище адіабати, протікають з підведенням теплоти до робочого тіла, а лівіше і нижче адіабати – з відведенням теплоти.

Для процесів, розміщених над ізотермою, характерно збільшення внутрішньої енергії газу і підвищення температури; процеси, розташовані під ізотермою, супроводжуються зменшенням внутрішньої енергії і температури.