ТОТ (лекции) / ТМО (лекц_я 14) нестац. тепл

14

Л е к ц і я 2.4. Теплопровідність при нестаціонарному режимі.

Нестаціонарні процеси теплообміну. Нагрівання (охолодження) тіл у середовищі з постійною температурою. Постановка задачі. Безрозмірна форма розв’язання задачі. Критерії Біо та Фур’є. Аналітичне розв’язання задачі нестаціонарної теплопровідності для плоскої стінки. Графічне розв’язання задачі. Аналіз рішення. Кількість теплоти процесу нагрівання (охолодження). Визначення температури тіл кінцевих розмірів.

Регулярний тепловий режим та його математичний опис. Темп охолодження та його визначення. Теореми Г.М. Кондрат’єва. Коефіцієнт нерівномірності розподілу температури. Коефіцієнт форми. Практичне застосування теорії регулярного режиму.

Методи розв’язання задач теплопровідності.

Джерела інформації: [1], с.339-347; [2], с.177-195; [8], с.220-244.

Нестаціонарні процеси теплообміну. Нагрівання (охолодження) тіл у середовищі з постійною температурою. Постановка задачі. Безрозмірна форма розв’язання задачі. Критерії Біо та Фур’є. В природі і техніці найчастіше мають місце нестаціонарні процеси теплообміну. Теплопровідність при нестаціонарному режимі зустрічаються при нагріванні або охолодженні різних об'єктів, при переходах з одного теплового режиму на інший режим. Нестаціонарні режими теплопровідності можуть бути перехідними або періодичними. Перехідні процеси характеризуються переходом від одного стаціонарного режиму до іншого стаціонарного режиму. Прикладом перехідних процесів може служити нагрівання (охолодження) тіл у газовому чи рідинному середовищі з постійною температурою. До перехідного процесу відноситься і розігрів опалювальних приладів до стаціонарного режиму. Періодичними режимами називають такі, при яких температура тіла коливається в часі за визначеним законом. Як приклад можна розглядати добову зміну температури зовнішнього повітря, що впливає на температуру конструкцій будинків. В інженерній практиці перехідні процеси зустрічаються частіше і тому ці процеси будуть вивчатися надалі. Формулювання задачі нестаціонарної теплопровідності здійснюють на основі математичної моделі. Математичні моделі явищ теплопровідності включають диференціальні рівняння основних досліджуваних процесів і рівняння для крайових (граничних і початкових) умов.

Методом рішення називають сукупність прийомів, які дозволяють одержати, виходячи з заданої математичної моделі, чисельні дані, що описують шукане температурне поле. Розв'язанням називають процес, заснований на відповідному методі, у результаті якого від математичної моделі можна перейти до шуканих значень температур.

Математичні моделі можуть бути лінійними і нелінійними. Лінійним називають рівняння, яке лінійне щодо невідомої функції (у даному випадку – температури) і її частинних похідних. Так, у лінійних рівняннях фізичні параметри, характерні для процесу теплопровідності (теплопровідність, теплоємність, температуропровідність) приймаються постійними, незалежними від шуканої функції (температури). Математична модель стає нелінійною, коли одне з її рівнянь нелінійне. Таким може бути рівняння теплопровідності, або рівняння, що входять у граничні умови. Одне з часто використовуваних способів розв'язання нелінійних рівнянь зводиться до зведення їх частково або цілком до лінійних, тобто до використання методу лінеаризації.

При розв'язанні математичної моделі в залежності від того, які величини приймаються заданими і які шуканими, досліджувані задачі можуть бути наступними. Мається математична модель і відомі значення фізичних величин, що входять у вихідне рівняння й у крайові умови. Визначення температурного поля ґрунтується на розв'язанні прямої задачі. Відома математична модель, а також температурне поле і коефіцієнти, що входять в основне рівняння. Необхідно визначити граничні умови. У такому випадку використовують методи рішення зворотних задач. Мається математична модель досліджуваного процесу теплопровідності, а також відомо температурне поле. Коефіцієнти, що входять в основне рівняння, визначаються розв'язанням інверсної задачі. У літературі зворотні й інверсні задачі найчастіше називають одним терміном – зворотними задачами.

На рис. 5.1 показані криві зміни температури тіла на його поверхні t_ст та в центрі t_ц при охолодженні у рідині з температурою t_р . Спочатку знижується температура на поверхні тіла, тоді як температура в його центрі якийсь час залишається незмінною. Наприкінці процесу температура в усіх точках тіла наближається до температури навколишнього середовища.

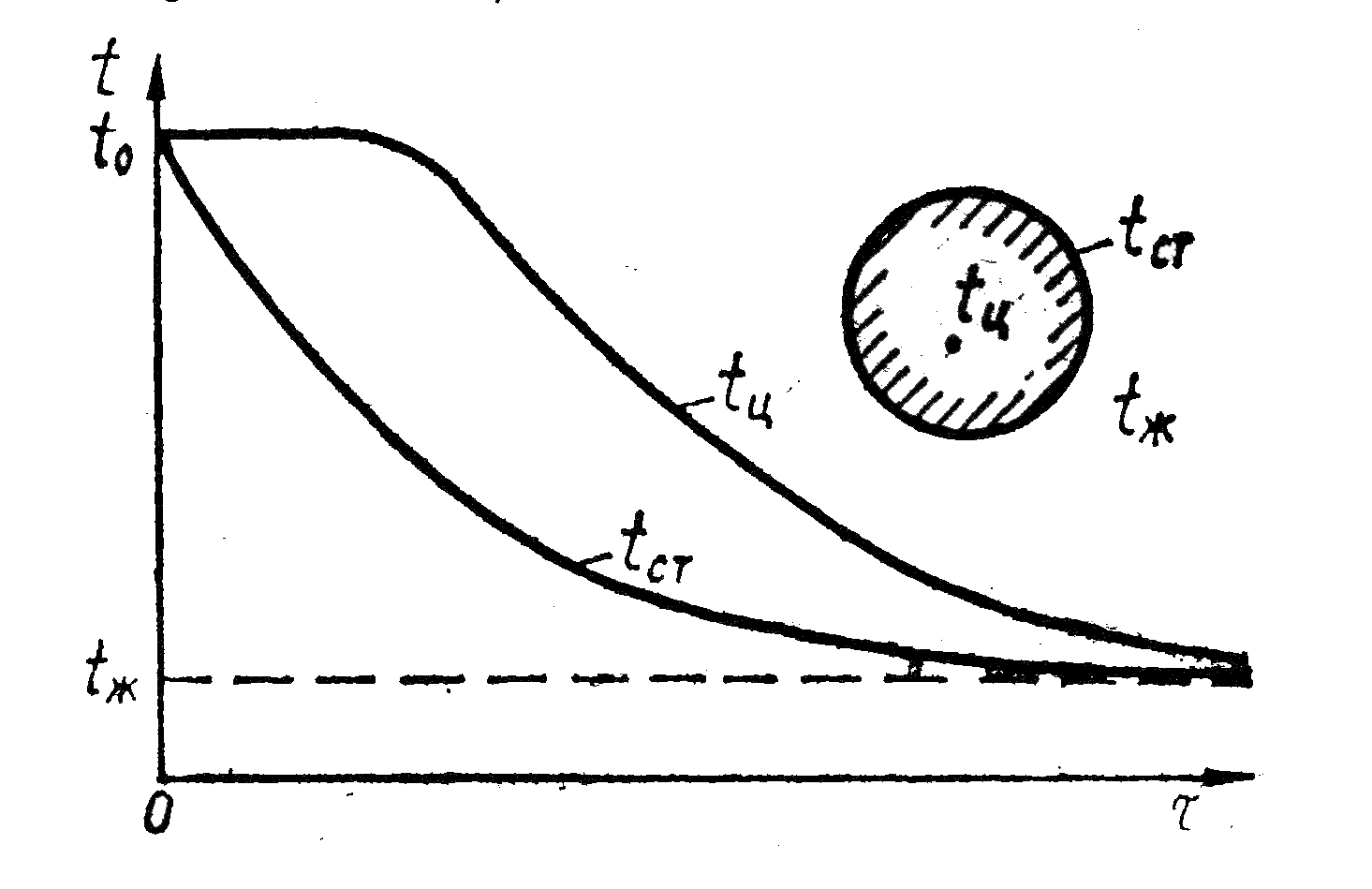
Рис. 5.1. Зміна температури тіла при охолодженні

Більшість задач нестаціонарної теплопровідності пов‘язана з визначенням температурного поля тіла і повної кількості теплоти, відданої або одержаної тілом за певний проміжок часу. В інших задачах необхідно знайти тривалість процесу, після закінчення якого температура тіла прийме наперед задане значення. Вирішення цих задач можна одержати аналітичним шляхом, тобто шляхом розв’язання диференціального рівняння теплопровідності з урахуванням крайових умов. Але таким шляхом можна розв’язати порівняно прості задачі. Для вирішення складніших задач застосовуються наближені методи.

Розглянемо умови подібності температурних полів при нестаціонарній теплопровідності. Диференціальне рівняння теплопровідності (4.1) в твердому тілі у випадку відсутності внутрішніх джерел теплоти має вид

. (5.1)

Виходячи з граничних умов третього роду, запишемо

, (5.2)

де – коефіцієнт теплопровідності тіла; – температурний градієнт на поверхні тіла.

У разі рівномірного температурного поля початкові умови такі: при . Позначимо надлишкову температуру в будь-якій точці тіла через . Тоді для точок, розташованих на поверхні і в центрі тіла, запишемо відповідно і . У початковий момент часу . Безрозмірна надлишкова температура . Безрозмірні координати точок: , де – характерний розмір тіла.

Приведемо рівняння (5.1) до безрозмірного виду. Записавши , , , і врахувавши, що , отримаємо

. (5.3)

Аналогічно попередньому

; ; . (5.4)

Підставивши вирази (5.3) і (5.4) в рівняння (5.1), отримаємо

. (5.5)

Отже для схожих точок тіла, у яких = idem, = idem і = idem, безрозмірна температура залежить від критерію (числа) Фур’є . Критерій Фур’є називають критерієм теплової гомохронності, що характеризує зв'язок між швидкістю зміни температурного поля, фізичними параметрами і розмірами тіла. Приведене до безрозмірного виду рівняння (5.2) дозволяє одержати критерій (число) Біо , яке визначає подібність процесів теплообміну на поверхні тіла. Він представляє собою відношення внутрішнього термічного опору теплопровідності до зовнішнього термічного опору тепловіддачі: .

В результаті спільного розв’язання рівнянь (5.1) і (5.2) з урахуванням умов однозначності, записаних у безрозмірному виді, отримаємо узагальнене рівняння для температурного поля

, (5.6)

вид якого залежить від форми тіла.

Аналітичне розв’язання задачі нестаціонарної теплопровідності для плоскої стінки. Графічне розв’язання задачі. Аналіз рішення. Розглянемо аналітичне розв’язання задачі нестаціонарної теплопровідності на прикладі охолодження (нагрівання) необмеженій стінки (пластини) за граничних умов третього роду (рис. 5.2).

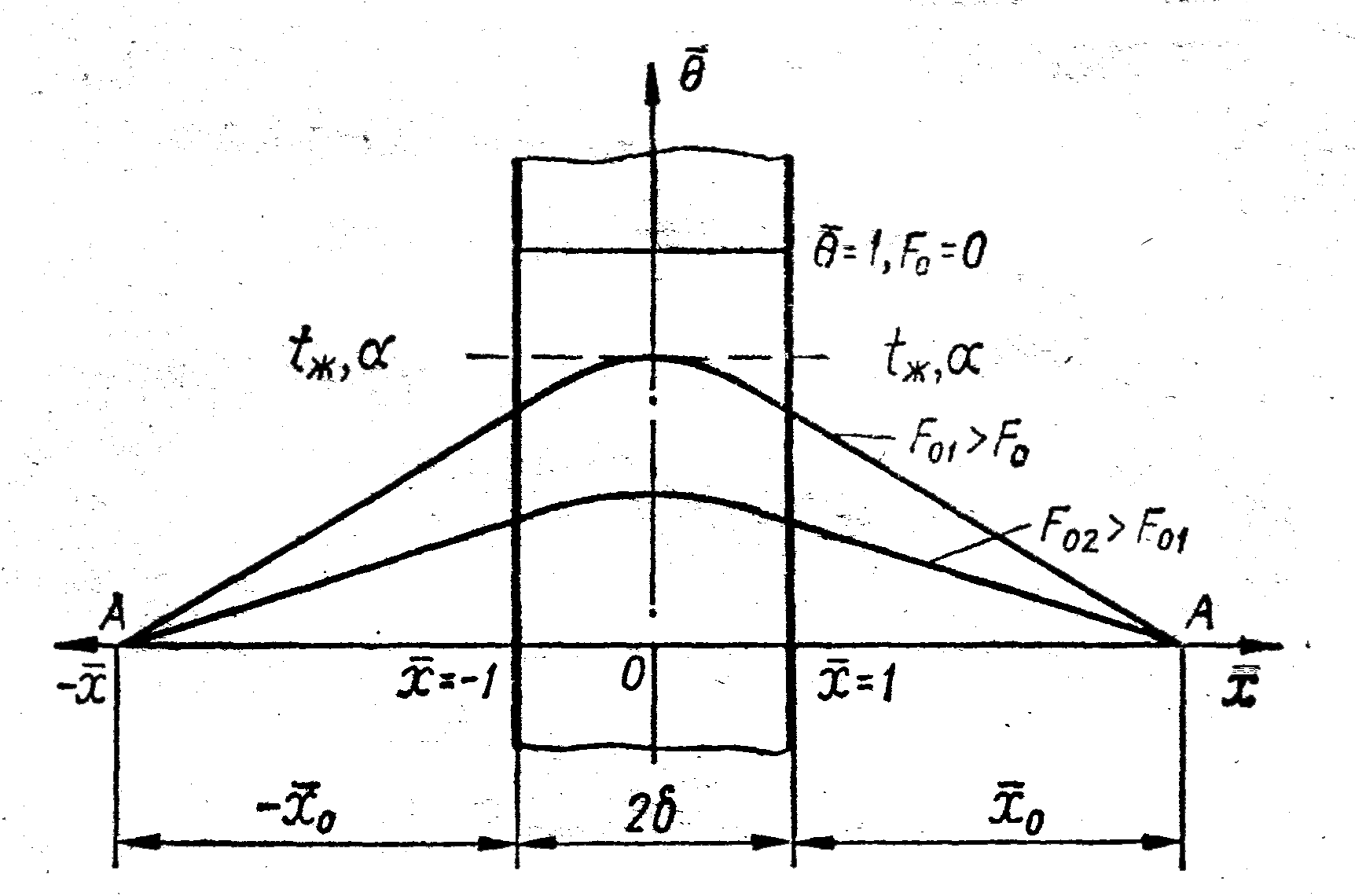
Рис. 5.2. Охолодження необмеженої пластини

У початковий момент часу () температура в пластині розподілена рівномірно і дорівнює . Задана температура навколишнього середовища < . Теплообмін з обох сторін пластини відбувається при постійному заданому коефіцієнті тепловіддачі . Задані також постійні фізичні параметри пластини . Вважаємо, що розміри пластини уздовж осей Оу і Оz настільки великі, що теплообміном з торців можна знехтувати. За таких умов температурне поле в пластині буде симетричним, тому її товщину зручно позначити 2. Диференціальне рівняння теплопровідності (5.1) для одновимірної задачі з урахуванням прийнятого раніше позначення надлишкової температури запишемо у виді

. (5.7)

Умови однозначності наступні. Початкові умови: при

; (5.8)

граничні умови: при

, (5.9)

де ;

умови симетрії температурного поля: при

. (5.10)

Для знаходження функції розподілу температури в пластині скористаємося методом розділення змінних, відповідно до якого рішення рівняння (6.7) відшукується у вигляді добутку двох функцій, одна з яких залежить тільки від просторової координати, а інша – від часу:

. (5.11)

Підставивши останній вираз в диференціальне рівняння (5.7) і розділивши змінні, одержимо

. (5.12)

Ліва частина цього рівняння залежить тільки від , права – від . Рівність (5.12) можлива у випадку, якщо обидві його частини дорівнюють постійній величині, яку позначимо . Тоді ця рівність прийме вид

. (5.13)

На підставі останньої рівності складемо два диференціальні рівняння:

; ,

рішення яких відомі:

Знак «мінус» при постійній вибраний з наступних міркувань: при температурна функція , а отже, також прямує до нуля, тобто забезпечується загасання процесу. Підставивши вирази і в (5.11), запишемо частинний розв’язок

. (5.14)

Вираз (5.14) задовольняє початковому диференціальному рівнянню (5.7) при будь-яких значеннях постійних , , і . Щоб вираз (5.14) був рішенням даної задачі, його слід підпорядкувати початковим і граничним умовам. З урахуванням умов симетрії (5.10) знаходимо

або

звідки = 0. Позначивши , вираз (5.14) перепишемо у вигляді

. (5.15)

Цей вираз задовольняє початковому рівнянню (5.7) і умовам симетрії при .

Підставивши вираз (5.15) в рівняння (5.9), отримаємо наступне рівняння:

,

після нескладних перетворень якого прийдемо до тригонометричного рівняння

. (5.16)

Розв’язання рівняння (5.16) дають точки перетину прямої і котангенсоїди (рис. 5.3), де і . З рисунка витікає, що рівняння (5.16) має безліч коренів , які залежать від порядкового номера n і числа Bi.

Кожному значенню відповідає частинне рішення, що задовольняє диференціальному рівнянню (5.7). Сума цих частинних рішень дає загальний розв’язок

,

де постійна , може бути знайдена з урахуванням початкових умов (5.8).

Рис. 5.3. До розв’язання рівняння для визначення

Остаточне рівняння для температурного поля в безрозмірній формі запишемо у вигляді [1]

(5.17)

де ; ; ;

. (5.18)

Аналіз рівняння (5.17) показує, що при достатньо великому проміжку часу, коли , ряд швидко збігається і може бути залишений тільки його перший член. В цьому випадку

. (5.19)

Використання рівняння (5.17) на практиці пов’язане з необхідністю виконання трудомістких розрахунків. Оскільки величина є функцією числа , з рівнянь (5.17) і (5.18) витікає, що при заданих координатах шукана безрозмірна температура залежить тільки від чисел і , тобто

. (5.20)

Для практичних розрахунків побудовані графіки цієї функції при і за допомогою яких можна визначити температури у середині і на зовнішній поверхні пластини (рис. 5.4) після закінчення заданого часу .

З метою приблизної побудови кривих розподілу температур в пластині розглянемо їх властивості. Проведемо дотичні до температурної кривої в точках (див. рис. 5.2). Вони проходять через дві направляючі точки А, які розташовані на відстані від поверхні пластини. Знайдемо значення . Для цього помножимо (5.9) на і отримаємо

.

З іншого боку,

,

звідки

. (5.21)

З останньої рівності витікає, що відстань точки А від поверхні визначається заданими умовами однозначності і не залежить від часу. Отже, дотичні до всіх температурних кривих в точках за незмінних граничних умов для будь-якого проміжку часу завжди проходитимуть через направляючі точки А. Це дозволяє побудувати графіки температурних кривих в пластині за знайденими значеннями температур в точках і . Чим менше число Bi, тим далі відстоїть точка А від поверхні пластини і тим менше відмінність між температурою поверхні і внутрішніх точок тіла.

Рис. 5.4. Графіки до визначення температури на поверхні пластини

Розглянемо три випадки:

1. При (практично ) направляюча точка А знаходиться на поверхні тіла, температура якої стає рівній температурі навколишнього середовища. Це означає, що точка перехрещення дотичних до температурних кривих знаходиться на поверхні пластини (рис. 5.5, б). З виразу для числа виходить: при заданих фізичних параметрах і товщині пластини, коли , тобто коли має місце велика інтенсивність відведення теплоти від поверхні. Інтенсивність процесу при цьому визначається тільки процесом теплопровідності в тілі і залежить як від фізичних властивостей, так і від розмірів тіла (внутрішня задача). При цьому (див. рис. 5.3). Як було зазначено, при ≥ 0,3 ряд (5.17) швидко збігається і помилка не перевищує 1 %, якщо відкинути всі члени, за винятком першого. При цих умовах , і для точки на осі пластини () рівняння (5.19) прийме вид

. (5.22)