Экономико-математические модели и методы проектного менеджмента

Лабораторная работа №5. Оптимізаційні задачі. Традиційні економічні задачі.

Лабораторна робота № 5 Тема. Оптимізаційні задачі. Традиційні економічні задачі.

1. Теоретичні відомості

Транспортна задача

Одну з традиційних задач економіки, транспортну задачу, можна вирішити за допомогою засобу Excel Поиск решения. Розглянемо приклад вирішення цієї задачі.

Нехай фірма має 4 фабрики і 5 центрів розподілу її товарів. Фабрики фірми розташовані в Полтаві, Чернігові, Миколаєві і Херсоні з обсягами виробництва 200, 150, 225 і 175 одиниць продукції щодня. Центри розподілу товарів фірми розташовані в Києві, Харкові, Донецьку, Одесі і Львові з обсягами споживання в 100, 200, 50, 250 і 150 одиниць продукції щодня. Збереження на фабриці одиниці продукції обходиться в 0,75 грн. у день. Штраф за прострочення постачання одиниці продукції складає 2,5 грн. у день. Вартість перевезення одиниці продукції наведено в табл.2.1.

Таблиця 1. Вартість перевезення одиниці продукції

Пункти виробництва	Центри розподілу					Обсяг виробництва
	Київ, b1	Харків, b2	Донецьк, b3	Одеса, b4	Львів, b5
	1	2	3	4	5
1. Полтава, a1	1,5	2	1,75	2,25	2,25	200
2. Чернігів, a2	2,5	2	1,75	1	1,5	150
3. Миколаїв, а3	2	1,5	1,5	1,75	1,75	225
4. Херсон, a4	2	0,5	1,75	1,75	1,75	175
Обсяг споживання	100	200	50	250	150	–

Необхідно так спланувати перевезення, щоб мінімізувати сумарні транспортні витрати.

Дана модель є збалансованою: сумарний обсяг зробленої продукції дорівнює сумарному обсягу споживання. Проте на практиці зустрічаються більш складні задачі, коли можливі як надвиробництво, так і дефіцит. У цих випадках необхідно було б увести:

– у випадку надвиробництва – фіктивний пункт розподілу, вартість перевезень одиниці продукції якого дорівнює вартості складування, а обсяги перевезень – обсягам складування надлишків продукції на фабриках;

– у випадку дефіциту – фіктивну фабрику, вартість перевезень одиниці продукції якої дорівнює вартості штрафів за недопостачання продукції, а обсяги перевезень – обсягам недопостачання продукції в пункти розподілу.

Невідомими в даній задачі є обсяги перевезень. Нехай xij – обсяг перевезень із i-ї фабрики в j-й центр розподілу. Сумарні транспортні витрати можна знайти з виразу

,

де сij – вартість перевезення одиниці продукції з i-ї фабрики в j-й центр споживання.

Невідомі в даній задачі повинні задовольняти таким обмеженням:

– обсяги перевезень не можуть бути негативними, тобто xij0;

– так як модель збалансована, то вся продукція повинна бути вивезена з фабрик, а потреби всіх центрів розподілу повинні бути цілком задоволені, тобто

Для вирішення цієї задачі за допомогою засобу Поиск решениявведемо дані, як показано на рис.1.

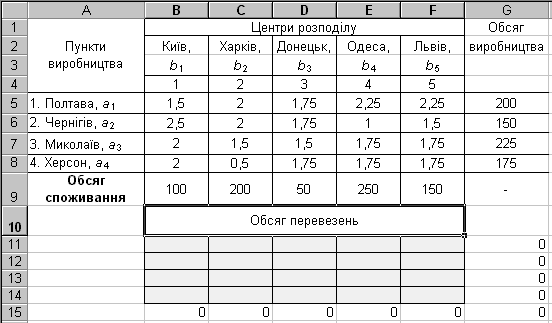
Рисунок 1. Вихідні дані транспортної задачі

У комірки B5:F8 введені вартості перевезень. Комірки B11:F14 відведені під значення невідомих обсягів перевезень. У комірки G5:G8 введені обсяги виробництва на фабриках, а в комірки B9:F9 введена потреба в продукції в пунктах розподілу. В комірку G15 введена цільова функція {=СУММПРОИЗВ (B5:F8;B11:F14)}.

У комірку B15 необхідно увести формулу {=СУМ(B11:B14)} і скопіювати її до комірки F15. Тоді в комірках B15:F15 будуть подані обсяги продукції, ввезеної в центри розподілу.

Аналогічно в комірку G11 необхідно ввести формулу {=СУМ(B11:F11)} і скопіювати її до комірки G14. Тоді в комірках G11:G14 буде знаходитися обсяг продукції, який вивозиться з фабрик.

Потім необхідно вибрати команду Сервис /Поиск решенияі заповнити діалогове вікно, що відкрилося, як показано на рис.2.

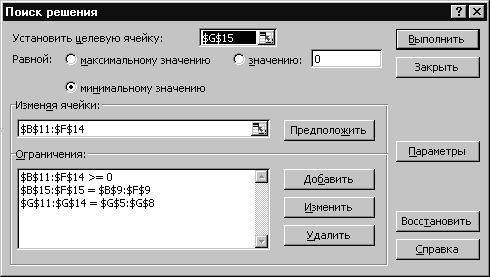
Рисунок2. Діалогове вікно Поиск решения для транспортної задачі

У діалоговому вікні Параметри поиска решенияважливо встановити прапорецьЛинейная модель. Після натискання кнопкиВыполнитьбуде знайдено оптимальний план постачань продукції і відповідні йому транспортні витрати. Результат рішення транспортної задачі поданий на рис.2.3.

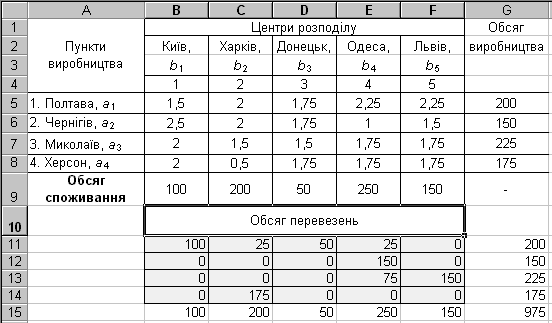
Рисунок 3. Оптимальне рішення транспортної задачі

Задача про призначення

Засіб Excel Поиск решения можна використовувати також для рішення ще однієї економічної задачі – задачі про призначення. Розгляньмо приклад її рішення. Нехай четверо робітників можуть виконувати чотири види роботи. Вартості с_ij виконання i-м робітником j-го виду роботи приведені в табл.2.

Таблиця 2. Вартість виконання робіт

Робітники	Види робіт
	1	2	3	4
1	8	6	2	5
2	5	2	9	8
3	3	8	1	9
4	1	4	2	3

Необхідно скласти такий план виконання робіт, щоб усі роботи були виконані, а кожний робітник був зайнятий тільки на одній роботі. Сумарна вартість виконання всіх робіт повинна бути мінімальною.

Дана модель є збалансованою, тобто число робіт збігається з числом робітників. У випадку незбалансованої моделі перед початком рішення її необхідно збалансувати, вводячи відсутнє число фіктивних рядків або стовпчиків із достатньо великими штрафними вартостями робіт.

При рішенні цієї задачі зручно використовувати таку таблицю xi: її рядки – номери робітників, а стовпчики - номери робіт. Тоді якщо i-й робітник виконує i–ту роботу, то ввести в комірку таблиці xij = 1. Якщо ні, тоді xij = 0. Інакше порядок заповнення таблиці можна представити так:

Тоді сумарну вартість виконання всіх робіт можна знайти з вираження

.

Невідомі в даній задачі повинні задовольняти таким обмеженням:

Для рішення цієї задачі за допомогою засобу Поиск решения введемо дані, як показано на рис.2.4.

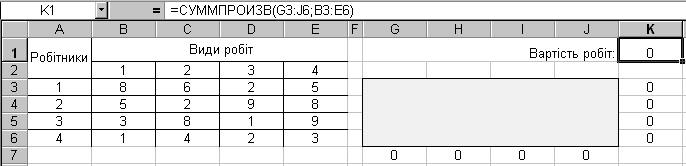
Рисунок 4. Вихідні дані задачі про призначення

У комірку K1 введемо цільову функцію {=СУММПРОИЗВ(G3:J6;B3:E6)}, що обчислює вартість робіт. У комірку G7 необхідно ввести формулу {=СУМ(G3:G6)} і скопіювати її до комірки J7,а в комірку K3 необхідно ввести формулу {=СУМ(G3:J3)} і скопіювати її до комірки K6. Тоді в комірках K3:K6, G7:J7 будуть задані ліві частини обмежень.

Потім необхідно вибрати команду Сервис, Поиск решения і заповнити діалогове вікно, що відкрилося, як показано на рис.2.5.

У діалоговому вікні Параметри поиска решения важливо встановити прапорець Линейная модель. Після натискання кнопки Выполнить засіб пошуку рішень знайде оптимальний план виконання робіт. Результати рішення задачі про призначення подані на рис.2.6.

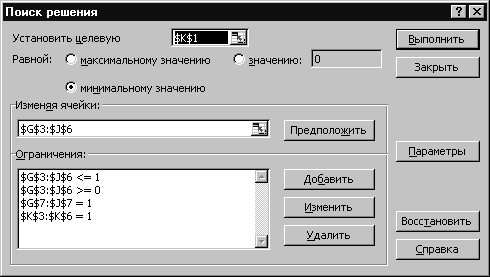
Рисунок 5. Діалогове вікно Поиск решения задачі про призначення

Рисунок 6. Оптимальний план робіт у задачі про призначення