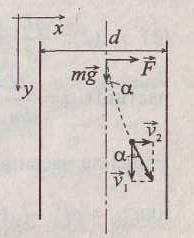- •Электричество
- •1. Закон Кулона и закон сохранения электрического заряда
- •Примеры решения задач
- •Дано Решение
- •Задачи для самостоятельного решения
- •2. Напряженность электрического поля
- •Напряженность и индукция электрических полей созданных телами различных конфигураций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Потенциал. Связь напряженности и потенциала
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4. Электроемкость
- •Электроемкости тел различной геометрической формы
- •Последовательное и параллельное соединение конденсаторов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5. Постоянный ток
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1 2 1 2
- •Магнетизм
- •6. Характеристики магнитного поля
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7. Работа и энергия магнитного поля
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •8. Электромагнитная индукция
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Ответы к задачам для самостоятельного решения
- •Приложения
- •Основные единицы измерения электрических и магнитных величин
- •Некоторые физические постоянные
- •Множители для образования десятичных кратных и дольных единиц
- •График зависимости индукции в от напряженности н магнитного поля для некоторого сорта железа
- •Диэлектрическая проницаемость диэлектриков (безразмерная величина)
- •Удельное сопротивление проводников (при 0°с), мкОм-м
3. Потенциал. Связь напряженности и потенциала
Потенциалом
 какой-либо точки электростатического
поля называется величина, равная
отношению потенциальной энергии
взаимодействия заряда с полем к величине
этого заряда:
какой-либо точки электростатического
поля называется величина, равная
отношению потенциальной энергии
взаимодействия заряда с полем к величине
этого заряда:
 .
(3.1)
.
(3.1)
Разностью потенциалов
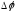 между точками
a
и b электрического
поля называется отношение работы А,
которую совершают электрические силы
при перемещении заряда q
из точки a
в точку b,
к этому заряду:
между точками
a
и b электрического
поля называется отношение работы А,
которую совершают электрические силы
при перемещении заряда q
из точки a
в точку b,
к этому заряду:
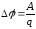 .
(3.2)
.
(3.2)
Работа А, совершаемая электрическими силами при перемещении заряда определяется по формуле:
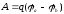 .
(3.3)
.
(3.3)
Потенциал электрического поля, создаваемого в данной точке несколькими точечными зарядами, равен алгебраической сумме потенциалов полей, создаваемых в этой точке каждым зарядом по отдельности:
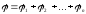 .
(3.5)
.
(3.5)
Связь между напряженностью и потенциалом электростатического поля:
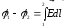 .
(3.6)
.
(3.6)
 .
.
Если φa и φb – потенциалы точек a и b, лежащих на одной линии напряженности в однородном электрическом поле на расстоянии r друг от друга, то напряженность электрического поля:
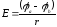 .
(3.7)
.
(3.7)
Используя интегральную связь (3.6), получаем формулы для расчета потенциала и разности потенциалов электрических полей, созданных зарядами, расположенными на телах разной геометрической формы (см. таблицу 2).
Таблица 2
Потенциал и разность потенциалов создаваемые телами различных конфигураций
|
Геометрическая форма заряженного тела |
|
|
|
|
Точечный заряд |
|
- |
|
|
Сфера |
|
const |
|
|
Сферический конденсатор |
const |
|
|
|
Бесконечная плоскость |
|
- |
|
|
Плоский конденсатор |
const |
|
|
|
Бесконечный цилиндр |
- |
|
|
|
Бесконечная нить |
- |
- |
|
|
Цилиндрический конденсатор |
const |
- |
|
Примеры решения задач
Задача
1.
В трех вершинах правильного шестиугольника
со стороной 10 см
находятся заряды
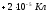 ,
, ,
,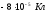 .
Определить потенциал в точкеА.
.
Определить потенциал в точкеА.
Дано:
Решение:
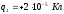 Потенциал
является энергетической характеристикой.
Потенциал
является энергетической характеристикой.
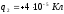 Потенциал результирующего поля
равен алгебраической
Потенциал результирующего поля
равен алгебраической
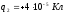 сумме
потенциалов, создаваемых в этой
точке каждым
сумме
потенциалов, создаваемых в этой
точке каждым
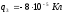 из
слагаемых полей.
из
слагаемых полей.
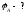
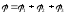
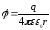 ,
,
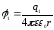 ,
,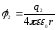 ,
,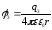 .
.
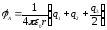
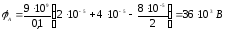
Ответ:
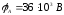
Задача 2.
Электростатическое
поле создано равномерно заряженной
сферической поверхностью радиуса R.
Заряд сферы q.
Найти разность потенциалов между двумя
точками, лежащими на расстоянии r1
и r2
от центра заряженной сферической
поверхности. Записать выражение
потенциала для точек внутри и вне и
построить график
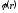 .
.
|
Дано: |
Решение: |
|
q
R
|
|
Рис. 8
Из условия симметрии
следует, что силовые линии электростатического
поля заряженной сферы направлены
радиально. По тем же причинам модуль
вектора напряженности
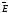 должен быть одинаковым во всех точках,
лежащих на одном и том же расстоянии от
центра заряженной сферы.
должен быть одинаковым во всех точках,
лежащих на одном и том же расстоянии от
центра заряженной сферы.
Если применить
теорему Гаусса для определения
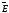 ,
то получим, что электростатическое поле
вне заряженной сферической поверхности
эквивалентно полю точечного заряда,
равного общему заряду и расположенного
в ее центре, и вычисляется по формуле:
,
то получим, что электростатическое поле
вне заряженной сферической поверхности
эквивалентно полю точечного заряда,
равного общему заряду и расположенного
в ее центре, и вычисляется по формуле:
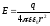 .
(1)
.
(1)
Внутри сферы поле отсутствует. В этом случае уравнение
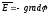 . (2)
. (2)
имеет вид:
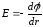 .
(3)
.
(3)
Формулы (1), (3) позволяют полностью решить задачу.
Из последнего уравнения следует, что
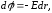 (4)
(4)
откуда
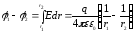 .
.
Окончательно запишем:
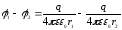 .
.
Найдем потенциал заряженной сферической поверхности:
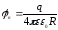
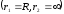 .
.
Потенциал вне сферы вычисляется по формуле:
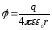
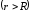 .
.
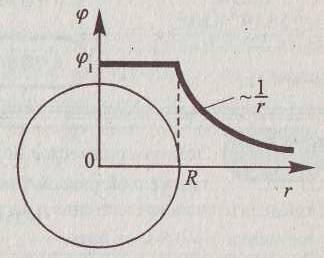
На рис.8 изображен
график
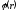 для заряженной сферической поверхности.
Вне сферы потенциал поля убывает
пропорционально
для заряженной сферической поверхности.
Вне сферы потенциал поля убывает
пропорционально ,
гдеr
– расстояние от центра заряженной сферы
до точки, в которой необходимо найти
потенциал. Внутри потенциал всех точек
одинаков и равен потенциалу заряженной
поверхности сферы.
,
гдеr
– расстояние от центра заряженной сферы
до точки, в которой необходимо найти
потенциал. Внутри потенциал всех точек
одинаков и равен потенциалу заряженной
поверхности сферы.
Ответ:
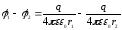 ,
,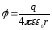 .
.
Задача 3.
Электрическое поле образовано двумя
параллельными пластинами, находящимися
на расстоянии d
= 2 см друг от друга. К пластинам
приложена разность потенциалов U
= 120 В. Какую скорость
 получит электрон под действием поля,
пройдя по линии напряженности расстояние
получит электрон под действием поля,
пройдя по линии напряженности расстояние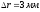 ?
?
|
Дано: |
Решение: |
|
d = 2 см U
= 120 В
|
Для
того, чтобы сообщить электрону
кинетическую энергию
|
Напряженность
поля
 ,
где
,
где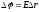 .
Тогда работа сил поля
.
Тогда работа сил поля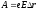 или, учитывая, что
или, учитывая, что .
Поскольку
.
Поскольку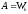 ,
то
,
то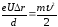 ,
откуда
,
откуда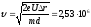 м/с.
м/с.
Ответ:
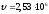 м/с.
м/с.
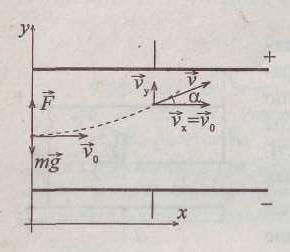
Задача 4. Электрон
с некоторой скоростью влетает в плоский
горизонтально расположенный конденсатор
параллельно пластинам на равном
расстоянии от них. Напряженность поля
в конденсаторе
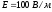 ;
расстояние между пластинами
;
расстояние между пластинами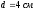 .
Через какое времяt
после того, как электрон влетел в
конденсатор, он попадет на одну из
пластин? На каком расстоянии s
от начала конденсатора электрон попадет
на пластину, если он ускорен разностью
потенциалов
.
Через какое времяt
после того, как электрон влетел в
конденсатор, он попадет на одну из
пластин? На каком расстоянии s
от начала конденсатора электрон попадет
на пластину, если он ускорен разностью
потенциалов
 ?
?
|
Дано:
|
Решение: |
|
t-? s -?
|
1.
Сделаем пояснительный чертеж.
|
Вдоль горизонтальной
оси движение электрона будет равномерным
со скоростью
 ,
т.к. вдоль осих
на него действуют силы. При равномерном
движении координата х
изменяется со временем х=
,
т.к. вдоль осих
на него действуют силы. При равномерном
движении координата х
изменяется со временем х=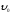 t.
Вдоль оси у
на электрон
действуют две силы: сила тяжести
t.
Вдоль оси у
на электрон
действуют две силы: сила тяжести
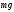 и сила электростатического поля
и сила электростатического поля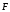 =e
=e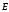 .
Сила тяжести
.
Сила тяжести
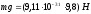 на тридцать порядков меньше
электростатической силы
на тридцать порядков меньше
электростатической силы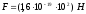 ,
и ею можно пренебречь. Под действием
электростатической силы движение
электрона вдоль осиу
будет
равноускоренным, а координата у
изменяется со временем по закону
,
и ею можно пренебречь. Под действием
электростатической силы движение
электрона вдоль осиу
будет
равноускоренным, а координата у
изменяется со временем по закону
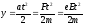 .
Отсюда приу
=
.
Отсюда приу
=
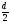 имеем
имеем
 .
Пройдя разность потенциаловU,
электрон за счет работы А
сил электростатического поля приобретает
кинетическую энергию, т.е.
.
Пройдя разность потенциаловU,
электрон за счет работы А
сил электростатического поля приобретает
кинетическую энергию, т.е.
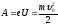 ,
откуда
,
откуда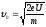 .
Тогда через времяt
=48 нс он упадет на пластину на расстоянии
.
Тогда через времяt
=48 нс он упадет на пластину на расстоянии
 .
Подставив числовые данные, получимS=22 см.
.
Подставив числовые данные, получимS=22 см.
Ответ: S=22 см.
Задача 5. Электрон
влетает в плоский горизонтально
расположенный конденсатор параллельно
его пластинам со скоростью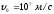 .
Напряженность поля в конденсаторе
.
Напряженность поля в конденсаторе ;
длина конденсатораl=5 см.
Найти модуль и направление скорости
;
длина конденсатораl=5 см.
Найти модуль и направление скорости
 электрона при вылете его из конденсатора.
электрона при вылете его из конденсатора.
|
Дано:
|
Решение: |
|
l=5 см
|
1. Сделаем пояснительный чертеж.
|
Полная скорость
электрона в момент вылета из конденсатора
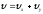 ,
где
,
где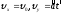 .
В скалярной форме
.
В скалярной форме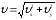 .
Поскольку
.
Поскольку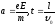 ,
то
,
то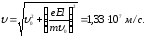 Направление скорости
Направление скорости электрона определяется углом
электрона определяется углом .
Из рисунка видно, чтоcos
.
Из рисунка видно, чтоcos =
=
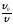 ;
;
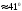 .
.
Ответ: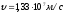 ,
,
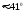 .
.
Задача 6. Между двумя вертикальными пластинами на одинаковом расстоянии от них падает пылинка. Вследствие сопротивления воздуха скорость пылинки постоянна и равна v1 = 2 см/с. Через какое время t после подачи на пластины разности потенциалов U = 3 кВ пылинка достигнет одной из пластин? Какое расстояние l по вертикали пылинка пролетит до попадания на пластину? Расстояние между пластинами d = 2 см, масса пылинки m = 2·10-9 г, заряд ее q = 6,5·10-17 Кл.
|
Дано: |
Решение: |
|
v1
= 2 см/с
U = 3 кВ d = 2 см m = 2·10-9 г q = 6,5·10-17 Кл t - ?
|
1. Сделаем пояснительный чертеж.
|
В отсутствие
электрического поля
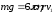 .
При наличии поля на пылинку действует
горизонтальная сила
.
При наличии поля на пылинку действует
горизонтальная сила
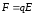 ,
которая сообщает пылинке ускорение,
но из-за сопротивления воздуха в
горизонтальном направлении также
устанавливается движение с некоторой
постоянной скоростью
,
которая сообщает пылинке ускорение,
но из-за сопротивления воздуха в
горизонтальном направлении также
устанавливается движение с некоторой
постоянной скоростью ,
причем
,
причем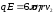 .
Из рисунка видно, что
.
Из рисунка видно, что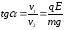 .
Кроме того, отношение
.
Кроме того, отношение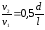 ,
откуда
,
откуда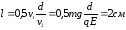 ,
тогда
,
тогда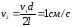 .
Искомое время найдем по формуле
.
Искомое время найдем по формуле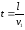 .
Подставляя числовые данные, получим
.
Подставляя числовые данные, получим
Ответ:
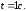

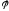 вне,
В
вне,
В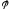 внутри,
В
внутри,
В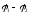 ,
В
,
В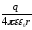

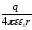
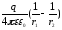
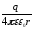 ,
,

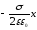
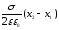
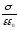 ,
,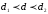
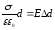
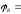 const
const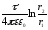
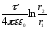
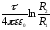
 ?
?
 -?
-? 
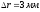
 -?
-? ,
силы электрического поля должны
совершить работу
,
силы электрического поля должны
совершить работу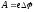 ,
где
,
где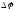 -
разность потенциалов между точками,
находящимися на расстоянии
-
разность потенциалов между точками,
находящимися на расстоянии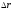 .
.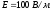
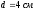
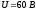

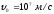
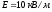
 -?
-?
 -?
-?