
- •Электричество
- •1. Закон Кулона и закон сохранения электрического заряда
- •Примеры решения задач
- •Дано Решение
- •Задачи для самостоятельного решения
- •2. Напряженность электрического поля
- •Напряженность и индукция электрических полей созданных телами различных конфигураций
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •3. Потенциал. Связь напряженности и потенциала
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •4. Электроемкость
- •Электроемкости тел различной геометрической формы
- •Последовательное и параллельное соединение конденсаторов
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •5. Постоянный ток
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •1 2 1 2
- •Магнетизм
- •6. Характеристики магнитного поля
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •7. Работа и энергия магнитного поля
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •8. Электромагнитная индукция
- •Примеры решения задач
- •Задачи для самостоятельного решения
- •Ответы к задачам для самостоятельного решения
- •Приложения
- •Основные единицы измерения электрических и магнитных величин
- •Некоторые физические постоянные
- •Множители для образования десятичных кратных и дольных единиц
- •График зависимости индукции в от напряженности н магнитного поля для некоторого сорта железа
- •Диэлектрическая проницаемость диэлектриков (безразмерная величина)
- •Удельное сопротивление проводников (при 0°с), мкОм-м
Примеры решения задач
Задача
1. В
трех вершинах правильного шестиугольника
со стороной 10 см
находятся
заряды 2∙10-5 Кл,
4∙10-5 Кл,
-8∙10-5 Кл.
Определить напряженность в точке А.

Дано:
Решение:
а
= 0,1 м 1. Сделаем пояснительный

q3=-8∙10-5 Кл чертеж.
q2=4∙10-5 Кл
q1=2∙10-5 Кл
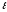 =1
=1
ЕА
-?
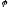 А-?
А-?
2. Применим принцип суперпозиции полей.
Напряженность поля зарядов q1, q2, q3 в точке А равна векторной сумме напряженностей полей, созданных в этой точке каждым зарядом в отдельности.
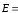
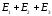 .
(1)
.
(1)
Напряженность поля, создаваемого точечным зарядом q на расстоянии r от заряда, равна:
 .
(2)
.
(2)
3.
Запишем
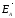 через компоненты
через компоненты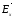 и
и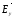 :
:
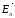 =
=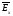 +
+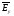 .
(3)
.
(3)
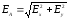 .
(4)
.
(4)
Проецируем (1) на оси х и у:
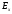 =
-
=
-
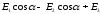
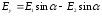 .
(5)
.
(5)
Подставим (5) в(4). Напряженность результирующего поля в точке А будет равна:
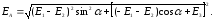 (6)
(6)
Поскольку числовые значения векторов напряженностей неизвестны, их нужно представить через заряды и расстояния. Напряженности полей зарядов q1, q2, q3 в точке А равны:
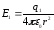 ;
;
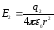 ;
;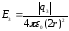 ,
так как
,
так как =1.
=1.
Знак заряда учли, когда выполняли чертеж. Подставляя эти выражения в формулу (6), будем иметь:
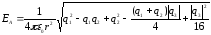 .
(7)
.
(7)
4. Подставляя численное значение в формулы (9) и (10), найдем:
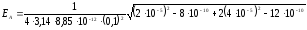 В/м
= = 18∙103 В/м.
В/м
= = 18∙103 В/м.
5. В каждой точке
электростатическое поле характеризуется
напряженностью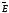 ,
которая является его силовой
характеристикой. Напряженность равна
геометрической сумме напряженностей
слагаемых полей.
,
которая является его силовой
характеристикой. Напряженность равна
геометрической сумме напряженностей
слагаемых полей.
Ответ:
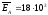 В/м.
В/м.
 Задача
2.
На рисунке АА
–
заряженная бесконечная плоскость с
поверхностной плотностью заряда
Задача
2.
На рисунке АА
–
заряженная бесконечная плоскость с
поверхностной плотностью заряда
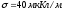 иВ
– одноименно заряженный шарик с массой
иВ
– одноименно заряженный шарик с массой
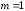 г
и зарядом
г
и зарядом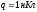 .
Какой угол
.
Какой угол с плоскостью
АА образует
нить, на которой висит шарик?
с плоскостью
АА образует
нить, на которой висит шарик?
Дано:
Решение:
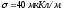 Заряженный
шарик находится в
Заряженный
шарик находится в
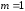 г
электрическом поле плоскости
г
электрическом поле плоскости
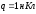 АА.
Напряженность поля
АА.
Напряженность поля
 -?
-?
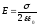 .
На шарик действуют
.
На шарик действуют

три силы: электростатическая
сила
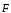 ,
сила натяжения нити
,
сила натяжения нити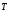
A
и
сила тяжести
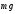 .
.
Условие равновесия
шарика
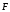 +
+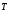 +
+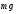 =0
или в проекциях на осьХ:
F-
T
sin
=0
или в проекциях на осьХ:
F-
T
sin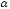 =0
(1), на ось У:
T
cos
=0
(1), на ось У:
T
cos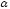 -mg=0
(2). Электростатическая сила
-mg=0
(2). Электростатическая сила
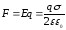 (3). Из (2) найдем
(3). Из (2) найдем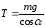 .
Подставляя это выражение в (1), получим
.
Подставляя это выражение в (1), получим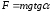 (4). Приравнивая правые части (3) и (4),
найдем
(4). Приравнивая правые части (3) и (4),
найдем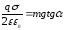 ,
откуда
,
откуда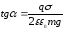 ;
;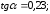
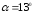 .
.
Ответ:
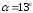 .
.
Задача 3. Заряд
15·10-9 Кл
равномерно распределен по тонкому
кольцу радиусом
 Найти напряженность электрического
поля в точке, находящейся на оси кольца
на расстоянии0,15 м
от его центра.
Найти напряженность электрического
поля в точке, находящейся на оси кольца
на расстоянии0,15 м
от его центра.
Дано:
Решение:
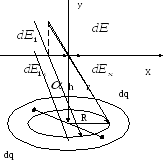
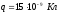 1. Сделаем
пояснительный чертеж.
1. Сделаем
пояснительный чертеж.
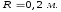
h
= 0,15
м
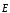 -
?
-
?
2.
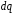 и
и - симметрично расположенные заряды,
которые можно считать точечными. В этих
условиях
- симметрично расположенные заряды,
которые можно считать точечными. В этих
условиях
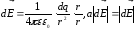 .
.
3. В проекциях на оси имеем
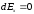 ,
,
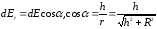 .
.
4.
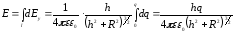 .
.
5.
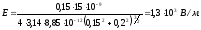
Ответ:
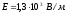
Задача 4. Три плоскопараллельные пластины, расположенные на малом расстоянии друг от друга, равномерно заряжены с поверхностной плотностью +3 · 10-8 Кл/м2, -5 · 10-8 Кл/м2, +8 · 10-8 Кл/м2. Найти напряженность поля в точках, лежащих между пластинами, и с внешней стороны. Построить график зависимости напряженности поля от расстояния, выбрав за начало отсчета положение первой пластины.
Дано:
Решение:
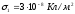 Согласно
принципу суперпозиции поле в любой
Согласно
принципу суперпозиции поле в любой
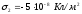 точке будет создаваться всеми тремя
заряженными
точке будет создаваться всеми тремя
заряженными
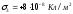 пластинами.
пластинами.
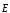 -?
-?
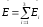 .
.
1. Сделаем пояснительный рисунок:

Для точки А:
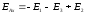 .
.
Для точки B:
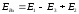 .
.
Для точки C:
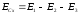 .
.
Для точки D:
 .
.
2. Для вычисления надо знать зависимость напряженности электростатического поля от плотности заряда на плоскости. Воспользуемся теоремой Остроградского-Гаусса.
Поток вектора
напряженности через замкнутую поверхность
определяется зарядом внутри этой
поверхности, деленным на произведение
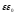 .
.
 .
(1)
.
(1)
В качестве замкнутой поверхности выбираем цилиндр с площадью основания S и образующей, параллельной линиям напряженности поля (рис.5).




Рис.5
Поток будет складываться из потока через боковую поверхность (ее линии напряженности не пронизывают) и через основания.
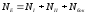 ,
,
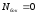 ,
,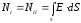 .
.
Из формулы (1) имеем
 ,
где
,
где
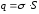 ,
,
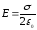 .
.
Так как плоскости
находятся в вакууме, то
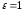 и
и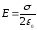 .
.
3. Рассчитаем напряженность электрического поля в точках A,B,C,D.
 ;
;
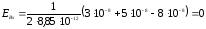 ;
;
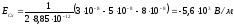 ;
;
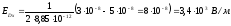 .
.
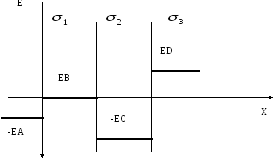
Рис. 6
Поле заряженной
плоскости является однородным.
Напряженность поля в каждой точке не
зависит от расстояния. На каждой
заряженной поверхности вектор
напряженности испытывает разрыв,
величина скачка которого определяется
отношением
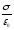 (рис.6).
(рис.6).
Ответ:
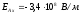 ,
,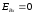 ,
,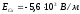 ,
, .
.
