2. Напряженность электрического поля

Электрические заряды создают в пространстве вокруг себя электрическое поле. На электрический заряд, помещенный в точку пространства, где есть электрическое поле, действует сила.

Электрическое поле в каждой точке пространства характеризуется напряженностью. Напряженностью электрического поля в данной точке называется отношение силы, действующей на помещенный в эту точку точечный зарядq, к этому заряду:

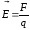. (2.1)

Напряженность электрического поля – векторная величина, направление которой совпадает с направлением силы приq>0. Если известна напряженность электрического поля в данной точке, то согласно формуле (1) на помещенный в эту точку заряд q действует сила:

. (2.2)

В диэлектриках электрическое поле характеризуется вектором электрической индукции , связанной с напряженностью электрического поля для изотропной среды соотношением:

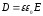. (2.3)

Напряженность электрического поля , создаваемая в данной точке несколькими точечными зарядами, равна векторной сумме напряженностей, создаваемых в этой точке каждым зарядом по отдельности (принцип суперпозиции):

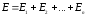. (2.4)

Таким образом, если электростатическое поле создано конечным числом электрических зарядов, то рассчитывать его напряженность следует, используя закон Кулона и принцип суперпозиции.

В случае создания поля заряженными телами с постоянной линейной плотностью (для нити), поверхностной плотностью (для цилиндрической, сферической или плоской поверхности) или объемной (для цилиндра, сферы или плоскости) используют теорему Остроградского-Гаусса.

Поток вектора напряженности электростатического поля через замкнутую поверхность в εε₀ раз меньше величины электрического заряда, находящегося внутри этой поверхности.

, где N_E – поток вектора напряженности

. (2.5)

Формулы для расчета напряженности и индукции электрических полей, созданных зарядами, расположенными на телах разной геометрической формы, приведены в таблице 1:

Таблица 1

Напряженность и индукция электрических полей созданных телами различных конфигураций

Геометрическая форма заряженного тела	Dвне,	Евне,	Dвнутри,	Евнутри,
Точечный заряд			_	_
Сфера			0	0
Сферический конденсатор	0	0
Бесконечная плоскость			_	_
Плоский конденсатор	0	0
Бесконечный цилиндр			0	0
Бесконечная нить			_	_
Цилиндрический конденсатор	0	0

где ε – диэлектрическая проницаемость среды, заполняющей пространство вокруг заряда;

σ – поверхностная плотность заряда: ,S – площадь поверхности заряженного тела;

τ – линейная плотность заряда: ,l – длина заряженного тела.